Introduction to Vibrations | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Introduction |

|
| Degrees of Freedom |

|
| Vibrational modes |

|
| Energetics |

|
| Interaction with Electromagnetic Radiation |

|
Introduction
We are familiar with resolving a translational vector into its three components along the x-, y-, and z- axes. Similarly a rotational motion can also be resolved into its components. Likewise the same is true for vibrational motion. The complex vibration that a molecule is making is really a superposition of a number of much simpler basic vibrations called “normal modes”. Before we take up any further description of “normal modes” it is necessary to discuss the degrees of freedom.
Degrees of Freedom
- Degree of freedom is the number of variables required to describe the motion of a particle completely. For an atom moving in 3-dimensional space, three coordinates are adequate so its degree of freedom is three. Its motion is purely translational. If we have a molecule made of N atoms (or ions), the degree of freedom becomes 3N, because each atom has 3 degrees of freedom.
- Furthermore, since these atoms are bonded together, all motions are not translational; some become rotational, some others vibration. For non-linear molecules, all rotational motions can be described in terms of rotations around 3 axes, the rotational degree of freedom is 3 and the remaining 3N-6 degrees of freedom constitute vibrational motion. For a linear molecule however, rotation around its own axis is no rotation because it leave the molecule unchanged. So there are only 2 rotational degrees of freedom for any linear molecule leaving 3N-5 degrees of freedom for vibration.
Vibrational modes
- A normal mode is a molecular vibration where some or all atoms vibrate together with the same frequency in a defined manner.
- Normal modes are basic vibrations in terms of which any other vibration is derived by superposing suitable modes in the required proportion.
- On the other hand, no normal mode is expressible in terms of any other normal mode. Each one is pure and has no component of any other normal mode (i.e. they are orthogonal to each other). Mathematically, the integral is
∫ψAψBdR = 0 (integration is done over the entire space) - The required number of “normal modes” is equal to the vibrational degree of freedom available so the number of modes for a nonlinear molecule is 3N−6 and that for a linear molecule is 3N−5 .
- Each mode has a definite frequency of vibration. Sometimes 2 or 3 modes may have the same frequency but that does not change the fact that they are distinct modes; these modes are called degenerate.
- Sometimes some modes are not IR active but they exist all the same. We shall revert back to the problem of IR activity and selection rules later.
The number of vibrational normal modes can be determined for any molecule from the formula given above. For a diatomic molecule, N = 2 so the number of modes is 3 × 2 − 5 = 1 . For a triatomic linear molecule (CO2), it is 3 × 3 − 5 = 4 and triatomic nonlinear molecule (H2O), it is 3 × 3 − 6 = 3 and so on.
Examples
Example 1: Water
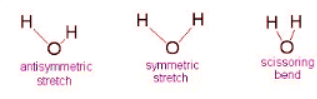
- The Symmetric Stretch (Example shown is an H2O molecule at 3685 cm-1)
- The Asymmetric Stretch (Example shown is an H2O molecule at 3506 cm-1)
- Bend (Example shown is an H2O molecule at 1885 cm-1)
A linear molecule will have another bend in a different plane that is degenerate or has the same energy. This accounts for the extra vibrational mode.
Example 2: Carbon Dioxide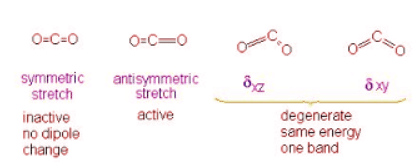
Example 3: The Methylene Group
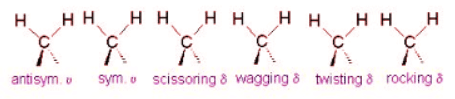
It is important to note that there are many different kinds of bends, but due to the limits of a 2-dimensional surface it is not possible to show the other ones.
The frequency of these vibrations depend on the inter atomic binding energy which determines the force needed to stretch or compress a bond. We discuss this problem in the next section. The determination of the nature of the relative displacement of each atom with respect to each other is more complicated and beyond the scope of this article. However, such motion can be seen in some common molecules as shown below.
Energetics
- For studying the energetics of molecular vibration we take the simplest example, a diatomic heteronuclear molecule AB. Homonuclear molecules are not IR active so they are not a good example to select. Let the respective masses of atoms A and B be mA and mB. So the reduced mass μAB is given by:

- The equilibrium internuclear distance is denoted by req. However as a result of molecular vibrations, the internuclear distance is continuously changing; let this distance be called r(t) . Let x(t) = r(t) − req . When x is non-zero, a restoring force F exists which tries to bring the molecule back to x = 0 , that is equilibrium. For small displacements this force can be taken to be proportional to x.

where k is the force constant. - The negative sign arises from the fact that the force acts in the direction opposite to x. This is indeed a case of Simple Harmonic Motion where the following well known relations hold.

where
- The potential energy is given by
 The total energy E (Kinetic + Potential) is obtained by solving the Schrödinger equation:
The total energy E (Kinetic + Potential) is obtained by solving the Schrödinger equation:
- A set of wave functions ψn) and the corresponding Eigenvalues En are obtained. En = (n + (1/2))hv where n is an integer (-1, 0, 1, 2 etc.). The energy is quantized, the levels are equally spaced, the lowest energy is (1/2)hv, and the spacing between adjacent levels is hv.
Interaction with Electromagnetic Radiation
As show above, the energy difference between adjacent vibrational energy levels is hvvibration. On the other hand, the photon energy is hvphoton. Energy conservation requires that the first condition for photon absorption be,
Hvvibration = hvphoton or vvibration = vphoton.
Such photons are in IR region of the electromagnetic spectrum. In addition, two more conditions must be met.
- For absorption of electromagnetic radiation, the dipole moment of the molecule must change with increasing internuclear separation resulting from the vibration (i.e, dμ/dD ≠ 0 ).
- The probability of a transition from one state to another is large if one of the state is odd and another even. This is possible if nfinal – ninitial = +1 (for absorption). At room temperature, modes are predominantly in energy state n = 0, so this transition is from n = 0 to n = 1, and ΔE = hν.
Applications
Spectroscopy in the IR region can determine the frequency and intensity of absorption. These frequencies are generally specific for a specific bonds such as c-c, c(double bond)c, c(triple bond)c, c-o, c(double bond)o, etc. So the IR absorption data is very useful in structure determination. The intensity depends on the concentration of the resposble spec. So it is useful for quantitative estimation and for identification.
Solved Examples
Example 1: Find the number of vibrational modes for the following molecules: NH3, C6H6, C10H8, CH4, C2H2 (linear).
Ans: NH3 – 6
C6H6 –30
C10H8 –48
CH4 –9
C2H2 – 7
Example 2: State which of the following vibrations are IR active: N2, CO, CO2 (stretching), HCl.
Ans: N2 – IR inactive
C0 – active
C02 (stretching) – inactive
HCl – active
Example 3: Calculate the vibrational frequency of CO given the following data: mass of C = 12.01 amu, mass of O = 16 amu, the force constant k = 1.86 × 103kg⋅s−2 .
Ans: mAB = mAxmB/(mA + mB) = 11.395 x 10-27
v = (1/2pi)(k/mAB).5 = 2143.3 cm-1
Example 4: Calculate the vibrational energy in Joules per mole of a normal mode in question 3, in its ground state of n = 0.
Ans: Energy of the mode for n = 0
E0 = (1/2)hv = 2.13 x 10-20J
Energy per mole = 2.13 x 10-20 x 6.022 x 1023 = 12.8KJ/mole
Example 5: Assuming the force constant to be the same for H2O and D2O . A normal mode for H2O is at 3650cm−1 . Do you expect the corresponding D2O wave number to be higher or lower?
Ans: v for D2O will be lower because v is inversely proportional to 1/(m.5), where m is the reduced mass.
FAQs on Introduction to Vibrations - Chemistry Optional Notes for UPSC
| 1. What are degrees of freedom in vibrational modes? |  |
| 2. What are vibrational modes in molecules? |  |
| 3. How does energy play a role in molecular vibrations? |  |
| 4. How do molecules interact with electromagnetic radiation? |  |
| 5. What is the significance of understanding molecular vibrations in various fields? |  |

|
Explore Courses for UPSC exam
|

|




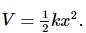 The total energy E (Kinetic + Potential) is obtained by solving the Schrödinger equation:
The total energy E (Kinetic + Potential) is obtained by solving the Schrödinger equation:
















