The Debye-Hückel Theory | Chemistry Optional Notes for UPSC PDF Download
The Debye-Hückel Theory
As ionic solutions are very common in chemistry, having to measure all activity coefficients ( γ± ) for all possible solute-solvent combinations is a pretty daunting task, even though in times past extensive tabulation has taken place. We should be grateful for the rich legacy that our predecessors have left us in this respect (it would be hard to get any funding to do such tedious work today). Of course, it would be very desirable to be able to calculate γ± values from first principles or if that fails by semi-empirical means. Fortunately, considerable progress has been made on this front as well. We can only scratch the surface of that topic in this course and will briefly discuss the simplest approach due to Debye and Hückel.
Debye and Hückel came up with a theoretical expression that makes is possible to predict mean ionic activity coefficients as sufficiently dilute concentrations. The theory considers the vicinity of each ion as an atmosphere-like cloud of charges of opposite sign that cancels out the charge of the central ion (Figure 25.6.1 ). From a distance the cloud looks neutral. The quantity 1/κ is a measure for the size of this cloud and κ is the Debye-length. Its size depends on the concentration of all other ions.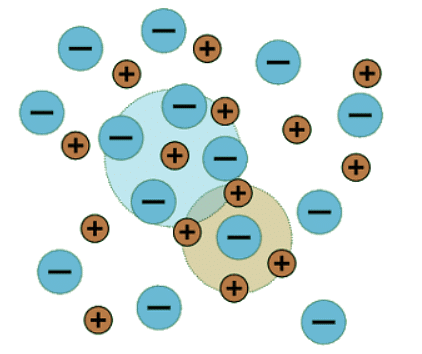 Figure 25.6.1: An idealized representation of a solution of a 1:1 electrolyte.
Figure 25.6.1: An idealized representation of a solution of a 1:1 electrolyte.
Ionic Strength
To take the effect from all other ions into account, it is useful to define the ionic strength (I) as: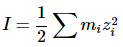
where mi is the molality of ion i and zi is its charge coefficient. Note that highly charged ions (e.g. z = 3+ ) contribute strongly (nine times more than +1 ions), but the formula is linear in the molality. Using the ionic strength the Debye-length becomes:
κ2 = constant I
The constant contains kT and εrεo in the denominator and the number of Avogadro NA and the square of the charge of the electron e in the numerator: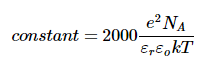
The Debye length and the logarithmic mean ionic activity coefficient are proportional:
ln γ ± ∝ κ
Again there are a number of factors in the proportionality constant: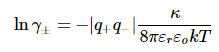
Note: The factors εr and εo are the relative permittivity of the medium and the permittivity of vacuum, respectively. Note that the factor 8πεrεo is specific to the SI system of units. In cgs units the expression would look different, because the permittivities are defined differently in that system.
If there is only one salt being dissolved, the ionic strength depends linearly on its concentration, the Debye length κ and lnγ±, therefore, go as the square root of concentration (usually molality):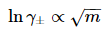
If there are other ions present the ionic strength involves all of them. This fact is sometimes used to keep ionic strength constant while changing the concentration of one particular ion. Say we wish to lower the concentration of Cu2+ in a redox reaction but we want to keep activity coefficients the same as much as possible. We could then replace it by an ion of the same charge say Zn2+ that does not partake in the reaction. A good way to do that is to dilute the copper solution with a zinc solution of the same concentration instead of with just solvent. The mean activity coefficient is given by the logarithm of this quantity as follows:
with:
where I is the ionic strength and a0 is a parameter that represents the distance of closest approach of ions. For aqueous solutions at 25 °C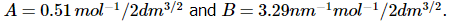
Unfortunately this theory only works at very low concentrations and is therefore also known as the Debye limiting law (Figure 25.6.2 ). There are a number of refinements that aim at extending the range of validity of the theory to be able to work at somewhat higher concentrations. These are discussed in the next section.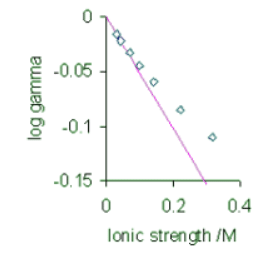 Figure 25.6.2: Experimental log γ± values for KBr at 25°C (points) and Debye–Hückel limiting law (coloured line)
Figure 25.6.2: Experimental log γ± values for KBr at 25°C (points) and Debye–Hückel limiting law (coloured line)
The most significant aspect of Equation 25.6.1 is the prediction that the mean activity coefficient is a function of ionic strength rather than the electrolyte concentration. For very low values of the ionic strength the value of the denominator in the expression above becomes nearly equal to one. In this situation the mean activity coefficient is proportional to the square root of the ionic strength.
Importance for Colloids
When a solid is formed by a reaction from solution it is sometimes possible that it remains dispersed as very small particles in the solvent. The sizes typically range in the nanometers This is why it has become fashionable to call them nanoparticles, although they had been known as colloidal particles since the mid nineteenth century. They are smaller than the wavelength of the visible reason. This causes liquids that contain them to remain clear, although they can at times be beautifully colored. A good example is the reduction of AuCl4- with citrate to metallic gold. This produces clear wine red solutions, even at tiny gold concentrations.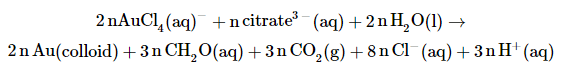
The reason the gold does not precipitate completely is typically that the nanoparticle (AuNP) formed during the reaction are charged by the attachment of some of the ionic species in solution to its surface. This results in an charged particle with an atmosphere with a certain Debye length around it (Figure 25.6.3 ). This charged cloud prevents the particle form coalescing with other particles by electrostatic repulsion.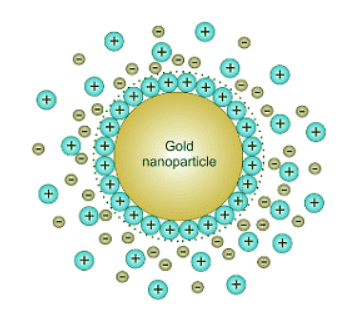 Figure 25.6.3: Potential difference as a function of distance from gold nanoparticle surface.
Figure 25.6.3: Potential difference as a function of distance from gold nanoparticle surface.
Such a system is called a colloid. Of course these systems are metastable. Often they have a pretty small threshold to crashing to a real precipitate under influence of the strong van der Waals interactions that the particles experience once they manage to get in close contact. Under the right conditions colloids can survive for a long time. Some gold colloids prepared by Faraday in the 1850's are still stable today.
It will be clear from the above that addition of a salt -particularly containing highly charged ions like 3+ or 3-- may destabilize the colloid because the ionic strength will changed drastically and this will affect the Debye length.
FAQs on The Debye-Hückel Theory - Chemistry Optional Notes for UPSC
| 1. What is the Debye-Hückel Theory? |  |
| 2. What is ionic strength? |  |
| 3. How does the Debye-Hückel Theory explain the behavior of electrolyte solutions? |  |
| 4. What is the importance of the Debye-Hückel Theory for colloids? |  |
| 5. Can the Debye-Hückel Theory be applied to all types of electrolyte solutions? |  |




















