[JEE Mains MCQs]
Q1: A block of mass m slides on the wooden wedge, which in turn slides backward on the horizontal surface. The acceleration of the block with respect to the wedge is : Given m = 8 kg, M = 16 kg Assume all the surfaces shown in the figure to be frictionless.
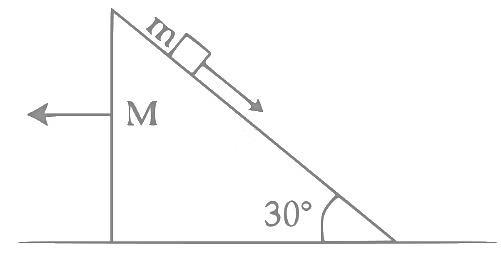 (a) 4/3 g
(a) 4/3 g
(b) 6/5 g
(c) 3/5 g
(d) 2/3 g
Ans: (d)
Let acceleration of wedge is aw and acceleration of block w.r.t. wedge is ab
For the wedge w.r.t. ground
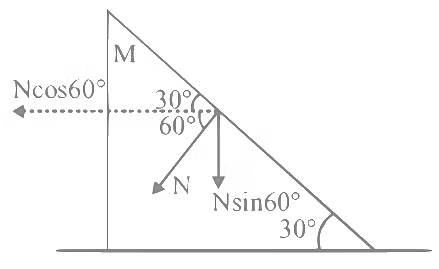 N cos60∘ = Maw = 16aw
N cos60∘ = Maw = 16aw
⇒ N = 32aw
F.B.D. of block w.r.t. wedge
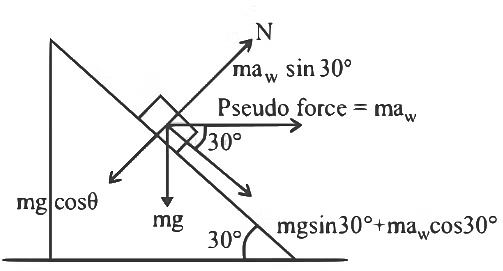 Balancing vertical forces
Balancing vertical forces

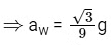
Along incline plane
8g sin30∘ + 8aw cos30∘ = mab = 8ab
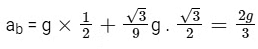
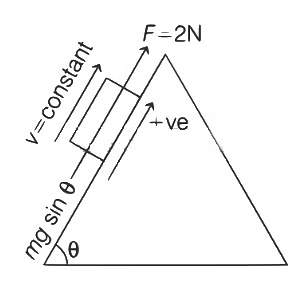
Q2: An object of mass 'm' is being moved with a constant velocity under the action of an applied force of 2N along a frictionless surface with following surface profile.
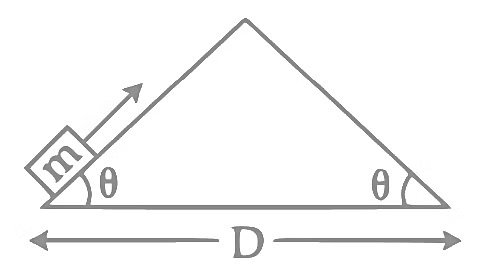 The correct applied force vs distance graph will be:
The correct applied force vs distance graph will be:
(a)
(b)

(c)
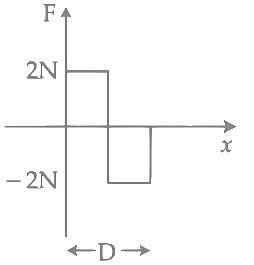
(d)
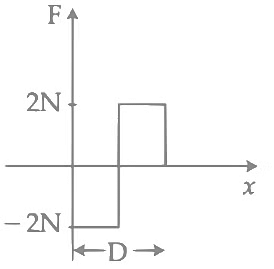
Ans: (c)
During upward motion
F = 2N = (+ve) constant
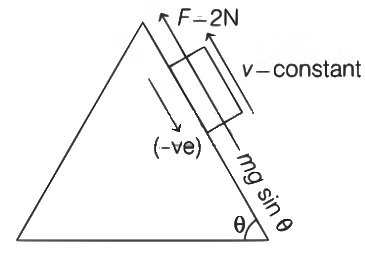
 During downward motion
During downward motion
⇒ F = 2N = (−ve) constant
 ⇒ Best possible answer is option (c)
⇒ Best possible answer is option (c)
Q3: Statement 1: If three forces 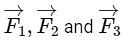 are represented by three sides of a triangle and
are represented by three sides of a triangle and 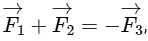 then these three forces are concurrent forces and satisfy the condition for equilibrium.
then these three forces are concurrent forces and satisfy the condition for equilibrium.
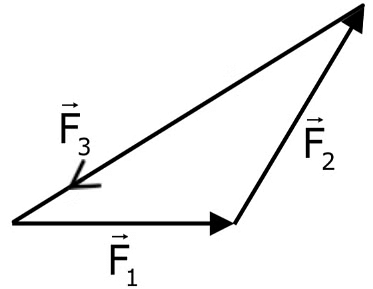
Statement 2: A triangle made up of three forces 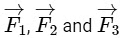 as its sides taken in the same order, satisfy the condition for translatory equilibrium.In the light of the above statements, choose the most appropriate answer from the options given below:(a) Statement - I is false but Statement - II is true
as its sides taken in the same order, satisfy the condition for translatory equilibrium.In the light of the above statements, choose the most appropriate answer from the options given below:(a) Statement - I is false but Statement - II is true
(b) Statement - I is true but Statement - II is false
(c) Both Statement-I and Statement-II are false
(d) Both Statement-I and Statement-II are true
Ans: (d)
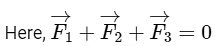
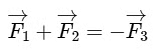
Both statements correct.
Q4: The boxes of masse 2 kg and 8 kg are connected by a massless string passing over smooth pulleys. Calculate the time taken by box of mass 8 kg to strike the ground starting from rest. (use g = 10 m/s2)
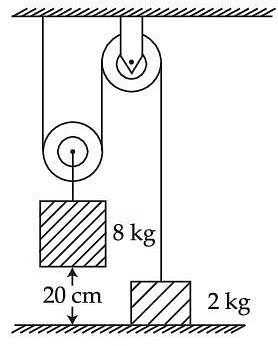 (a) 0.34 s
(a) 0.34 s
(b) 0.2 s
(c) 0.25 s
(d) 0.4 s
Ans: (d)
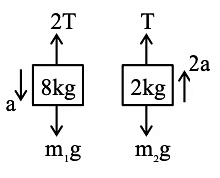 (m1g − 2T) = m1a − (1)
(m1g − 2T) = m1a − (1)
T − m2g = m2(2a)
2T − 2m2g = 4m2 a − (2)
m1g − 2m2g = (m1 + 4m2) a
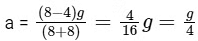
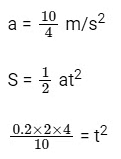
t = 0.4 sec
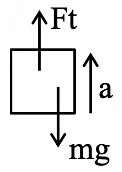
Q5: The initial mass of a rocket is 1000 kg. Calculate at what rate the fuel should be burnt so that the rocket is given an acceleration of 20 ms-2. The gases come out at a relative speed of 500 ms−1 with respect to the rocket : [Use g = 10 m/s2]
(a) 6.0 × 102 kg s−1
(b) 500 kg s−1
(c) 10 kg s−1
(d) 60 kg s−1
Ans: (d)
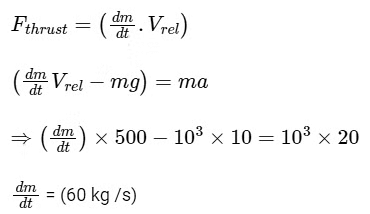
Q6: A particle of mass M originally at rest is subjected to a force whose direction is constant but magnitude varies with time according to the relation
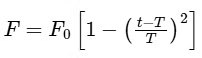
Where F0 and T are constants. The force acts only for the time interval 2T. The velocity v of the particle after time 2T is :
(a) 2F0T/M
(b) F0T/2M
(c) 4F0T/3M
(d) F0T/3M
Ans: (c)
At t = 0, u = 0

Q7: A force 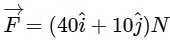 acts on a body of mass 5 kg. If the body starts from rest, its position vector
acts on a body of mass 5 kg. If the body starts from rest, its position vector 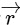 at time t = 10 s, will be
at time t = 10 s, will be
(a) 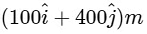
(b) 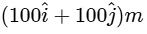
(c) 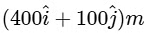
(d) 
Ans: (c)
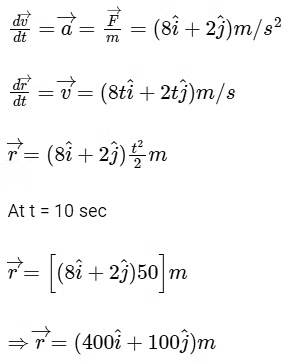
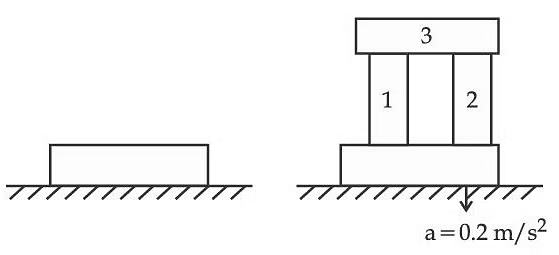
Q8: A steel block of 10 kg rests on a horizontal floor as shown. When three iron cylinders are placed on it as shown, the block and cylinders go down with an acceleration 0.2 m/s2. The normal reaction R' by the floor if mass of the iron cylinders are equal and of 20 kg each, is ____________ N. [Take g = 10 m/s2 and μs = 0.2]
 (a) 686
(a) 686
(b) 684
(c) 714
(d) 716
Ans: (a)
The force equation in vertical direction is
Mg − R = Ma
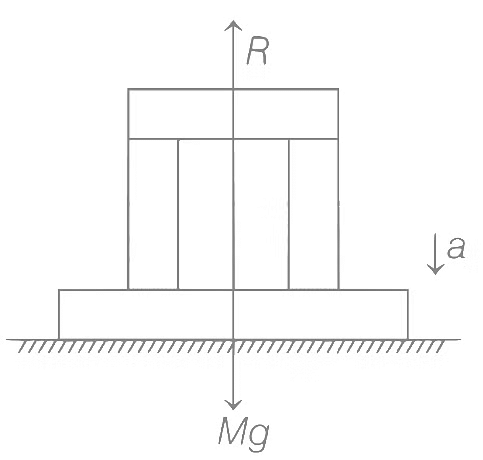 where,
where,
M = collective mass of block and all three iron cylinders = 10 + 3 × 20 = 70 kg
a = acceleration of block = 0.2 ms−2
g = 10 ms−2 and μs = 0.2
and R = normal reaction
Force along vertical axis Mg − R = Ma
∴ 70g − R = 70 × 0.2
⇒ R = 70 × 10 − 14
= 700 − 14 = 686 N
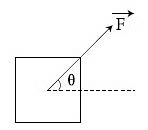
Q9: A block of mass m slides along a floor while a force of magnitude F is applied to it at an angle θ as shown in figure. The coefficient of kinetic friction is μk. then, the block's acceleration 'a' is given by:
(g is acceleration due to gravity)
 (a)
(a) 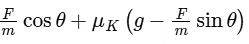
(b) 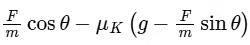
(c) 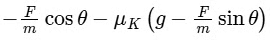
(d) 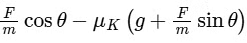
Ans: (b)
Drawing the FBD of the block.
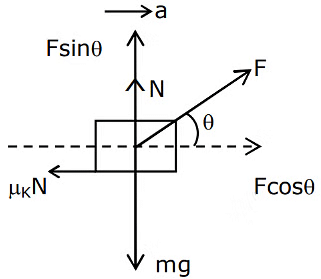 ⇒ N = mg − Fsinθ ..... (1)
⇒ N = mg − Fsinθ ..... (1)
Also, Fcosθ − μkN = m . a ..... (2)
Substituting the value of N from eq. (1) in eq. (2)
⇒ Fcosθ − μk(mg − Fsinθ) = m . a
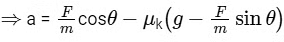
Q10: Two masses A and B, each of mass M are fixed together by a massless spring. A force acts on the mass B as shown in the figure. If the mass A starts moving away from mass B with acceleration 'a', then the acceleration of mass B will be:
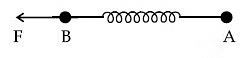 (a)
(a) 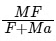
(b) 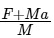
(c) 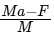
(d) 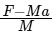
Ans: (d)
Let spring force acting on the both block is Fs.
F.B.D. of Block A
 ∴ Fs = Ma ..... (i)
∴ Fs = Ma ..... (i)
F.B.D. of Block B,
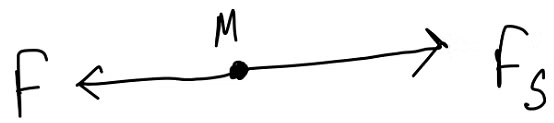 ∴ Acceleration of Block B,
∴ Acceleration of Block B,
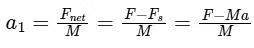
Q11: A particle is projected with velocity v0 along x-axis. A damping force is acting on the particle which is proportional to the square of the distance from the origin i.e. ma = − αx2. The distance at which the particle stops:
(a) 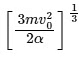
(b) 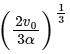
(c) 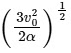
(d) 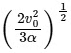
Ans: (a)
Given, speed of projection = v0
Damping force, F = ma = − αx2
⇒ a = − αx2 / m
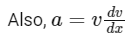
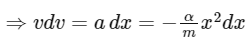
Integrating both sides, we get
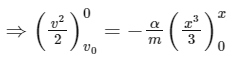
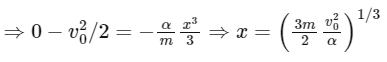
[JEE Mains Numericals]
Q12: When a body slides down from rest along a smooth inclined plane making an angle of 30∘ with the horizontal, it takes time T. When the same body slides down from the rest along a rough inclined plane making the same angle and through the same distance, it takes time αT, where α is a constant greater than 1. The co-efficient of friction between the body and the rough plane is 
Ans: 3
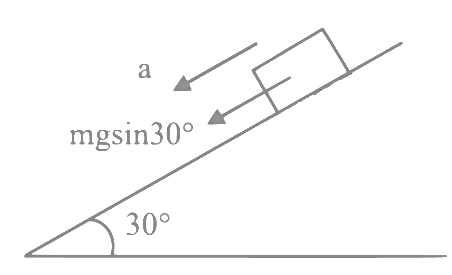 On smooth incline
On smooth incline
a = g sin30∘
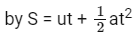
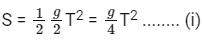
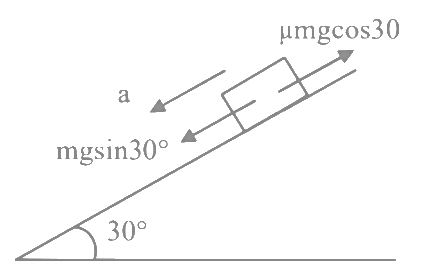 For rough surface,
For rough surface,
ma = mg sin30∘ − μmg cos 30∘
a = g sin30∘ − μg cos30∘
Distance covered by the block on the rough surface in time αT,
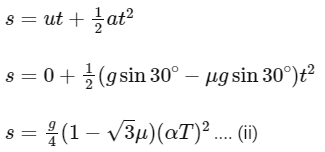
Distance covered by the block is same for both the case,
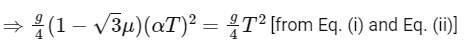
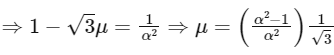
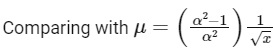
The value of the x = 3.
Q13: A car is moving on a plane inclined at 30∘ to the horizontal with an acceleration of 10 ms−2 parallel to the plane upward. A bob is suspended by a string from the roof of the car. The angle in degrees which the string makes with the vertical is ______________. (Take g = 10 ms−2)
Ans: 30
Given,
Angle of inclination, θ = 30∘
Acceleration, a = 10 ms−2
Acceleration due to gravity, g = 10 ms−2
According to the question the car and bob is as shown below,
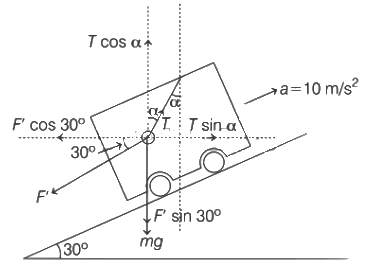 Here, F' is the pseudo force acting on the bob when we considered it from car's frame and T is the tension on the string.
Here, F' is the pseudo force acting on the bob when we considered it from car's frame and T is the tension on the string.
In equilibrium, ΣFx = 0 and ΣFy =
⇒ F' cos30∘ = T sinα
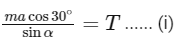
where, m is the mass of the bob.
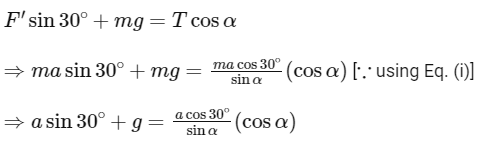
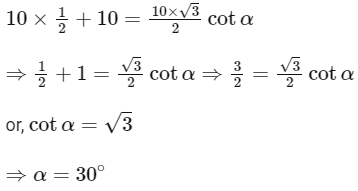
Q14: The coefficient of static friction between two blocks is 0.5 and the table is smooth. The maximum horizontal force that can be applied to move the blocks together is _______ N. (take g = 10 ms-2)
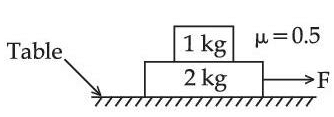 Ans: 15
Ans: 15
F = 3a (For system) ............ (i)
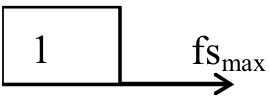 fsmax = 1a (for 1 kg block) ............ (ii)
fsmax = 1a (for 1 kg block) ............ (ii)
μ × 1 × g = a
F = 15N
Q15: A body of mass 'm' is launched up on a rough inclined plane making an angle of 30 ∘ with the horizontal. The coefficient of friction between the body and plane is 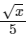 if the time of ascent is half of the time of descent. The value of x is __________.
if the time of ascent is half of the time of descent. The value of x is __________.
Ans: 3
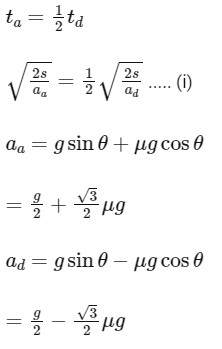
using the above values of aa and ad and putting in equation (i) we will gate μ = 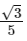
Q16: A bullet of mass 0.1 kg is fired on a wooden block to pierce through it, but it stops after moving a distance of 50 cm into it. If the velocity of bullet before hitting the wood is 10 m/s and it slows down with uniform deceleration, then the magnitude of effective retarding force on the bullet is 'x' N. The value of 'x' to the nearest integer is __________.
Ans: 10
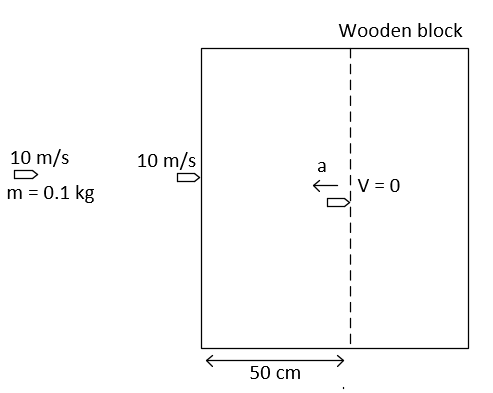
Mbullet = 0.1 kg
V2 = 44 + 2(−a) × 5
⇒ 0 = (10)2 − 2a × (0.5)
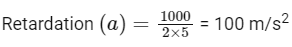
Retarding force (F) = ma = 0.1 × 100
FR = 10 N
Q17: A boy of mass 4 kg is standing on a piece of wood having mass 5 kg. If the coefficient of friction between the wood and the floor is 0.5, the maximum force that the boy can exert on the rope so that the piece of wood does not move from its place is __________ N. (Round off to the Nearest Integer) [Take g = 10 ms-2]
 Ans: 30
Ans: 30
 ∵ f = T
∵ f = T
⇒ μN = T
⇒ μ(90 − T) = T
⇒ 0.5 (90 − T) = T
⇒ 90 − T = 2T
⇒ 3T = 90
⇒ T = 30 N
Q18: A body of mass 1 kg rests on a horizontal floor with which it has a coefficient of static friction 1/√3. It is desired to make the body move by applying the minimum possible force F N. The value of F will be ____________. (Round off to the Nearest Integer) [Take g = 10 ms−2 ]
Ans: 5
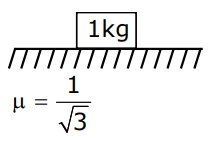 Minimum possible force ⇒
Minimum possible force ⇒
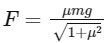
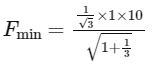
Fmin = 5N
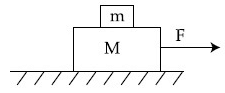
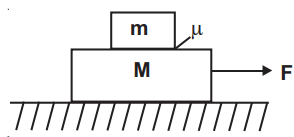
Q19: Two blocks (m = 0.5 kg and M = 4.5 kg) are arranged on a horizontal frictionless table as shown in figure. The coefficient of static friction between the two blocks is 3/7. Then the maximum horizontal force that can be applied on the larger block so that the blocks move together is ___________ N. (Round off to the Nearest Integer) [Take g as 9.8 ms−2]
 Ans:
Ans:
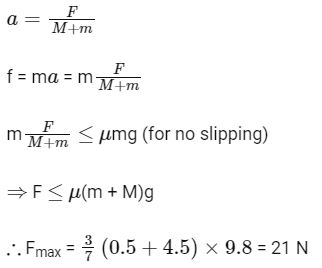
Q20: A body of mass 2 kg moves under a force of 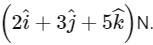 It starts from rest and was at the origin initially. After 4s, its new coordinates are (8, b, 20). The value of b is _____________. (Round off to the Nearest Integer)
It starts from rest and was at the origin initially. After 4s, its new coordinates are (8, b, 20). The value of b is _____________. (Round off to the Nearest Integer)
Ans: 12
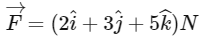
time = 4 sec
As body start from rest therefore position vector initially 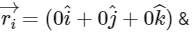 u (initial velocity) = 0
u (initial velocity) = 0
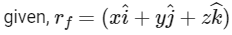
Now, from second equation of motion
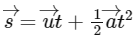
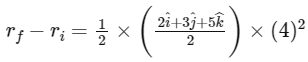

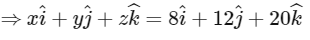
∴ The value of b = 12
Q21: A person standing on a spring balance inside a stationary lift measures 60 kg. The weight of that person if the lift descends with uniform downward acceleration of 1.8 m/s2 will be ______________ N. [g = 10 m/s2]
Ans: 492
The apparent weight Wapp of a person in an elevator moving with acceleration is given by:
Wapp = m(g − a)
where:
Wapp is the apparent weight,
m is the mass of the person,
g is the acceleration due to gravity,
a is the acceleration of the elevator.
Given that the person's mass is 60 kg, the acceleration due to gravity is 10 m/s², and the acceleration of the lift is 1.8 m/s², we can substitute these values into the formula:
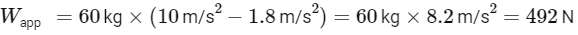
So, the apparent weight of the person when the lift descends with a uniform downward acceleration of 1.8 m/s² will be 492 N.
Q22: A boy pushes a box of mass 2 kg with a force 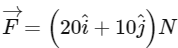 on a frictionless surface. If the box was initially at rest, then ___________ m is displacement along the x-axis after 10s.
on a frictionless surface. If the box was initially at rest, then ___________ m is displacement along the x-axis after 10s.
Ans: 500
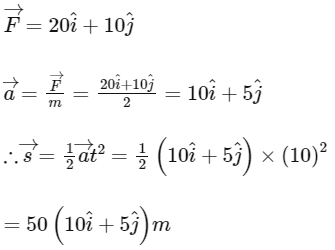
∴ Displacement along x-axis
= 50 × 10 = 500 m
Q21: As shown in the figure, a block of mass √3 kg is kept on a horizontal rough surface of coefficient of friction 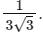 The critical force to be applied on the vertical surface as shown at an angle 60∘ with horizontal such that it does not move, will be 3x. The value of x will be _________.
The critical force to be applied on the vertical surface as shown at an angle 60∘ with horizontal such that it does not move, will be 3x. The value of x will be _________.
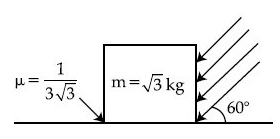 Ans: 3.33
Ans: 3.33
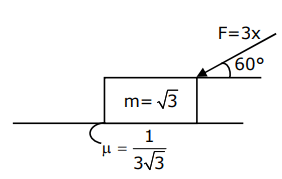
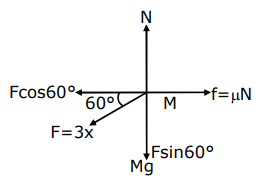 N = Mg + Fsin60∘
N = Mg + Fsin60∘
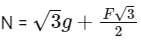
For No slipping
F cos 60∘ = Friction
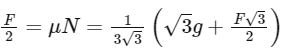
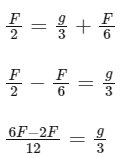
4F = 4g
F = 10
F = 3x
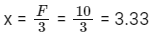
x = 3.33
Q22: An inclined plane is bent in such a way that the vertical cross-section is given by y = x2/ 4 where y is in vertical and x in horizontal direction. If the upper surface of this curved plane is rough with coefficient of friction μ = 0.5, the maximum height in cm at which a stationary block will not slip downward is _________ cm.
Ans: 25
The graph for given equation is shown below
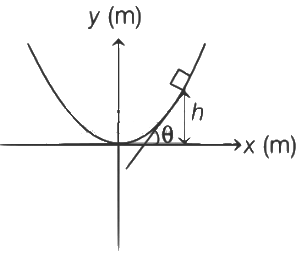 At maximum height, the slope of tangent drawn,
At maximum height, the slope of tangent drawn,
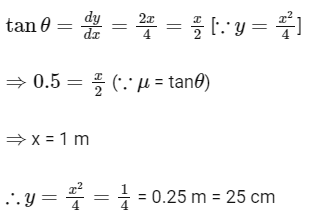
Q23: The coefficient of static friction between a wooden block of mass 0.5 kg and a vertical rough wall is 0.2. The magnitude of horizontal force that should be applied on the block to keep it adhere to the wall will be _________ N. [g = 10 ms−2]
Ans: 25
Given, coefficient of static friction, μs = 0.2
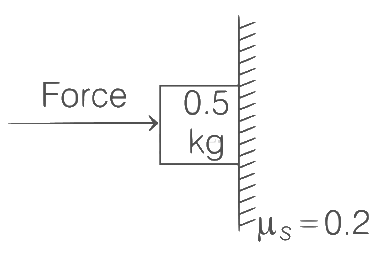 Various forces acting on block are shown below
Various forces acting on block are shown below
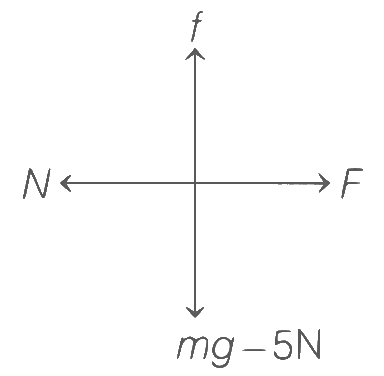 Frictional force ≤ mg
Frictional force ≤ mg
⇒ N × 0.2 ≤ 5
⇒ N ≤ 25
∴ Magnitude of horizontal force, F = N = 25 N
 (a) 4/3 g
(a) 4/3 g N cos60∘ = Maw = 16aw
N cos60∘ = Maw = 16aw Balancing vertical forces
Balancing vertical forces
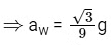
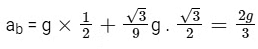
 The correct applied force vs distance graph will be:
The correct applied force vs distance graph will be:



 During downward motion
During downward motion ⇒ Best possible answer is option (c)
⇒ Best possible answer is option (c)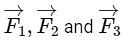 are represented by three sides of a triangle and
are represented by three sides of a triangle and 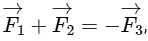 then these three forces are concurrent forces and satisfy the condition for equilibrium.
then these three forces are concurrent forces and satisfy the condition for equilibrium.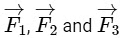 as its sides taken in the same order, satisfy the condition for translatory equilibrium.In the light of the above statements, choose the most appropriate answer from the options given below:(a) Statement - I is false but Statement - II is true
as its sides taken in the same order, satisfy the condition for translatory equilibrium.In the light of the above statements, choose the most appropriate answer from the options given below:(a) Statement - I is false but Statement - II is true
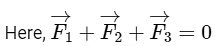
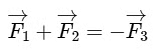
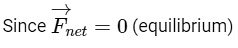
 (a) 0.34 s
(a) 0.34 s (m1g − 2T) = m1a − (1)
(m1g − 2T) = m1a − (1)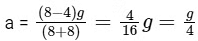
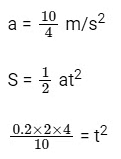

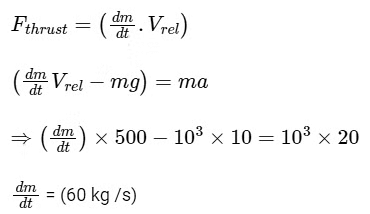
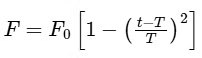

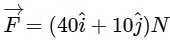 acts on a body of mass 5 kg. If the body starts from rest, its position vector
acts on a body of mass 5 kg. If the body starts from rest, its position vector 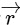 at time t = 10 s, will be
at time t = 10 s, will be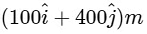
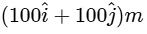
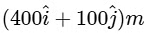

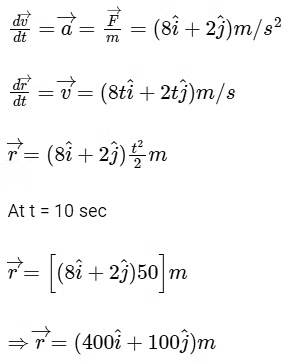
 (a) 686
(a) 686 where,
where, (a)
(a) 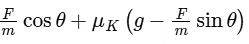
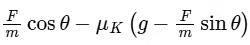
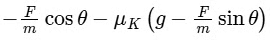
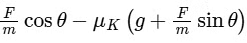
 ⇒ N = mg − Fsinθ ..... (1)
⇒ N = mg − Fsinθ ..... (1)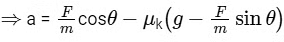
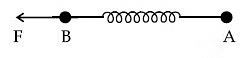 (a)
(a) 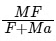
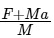
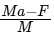
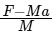
 ∴ Fs = Ma ..... (i)
∴ Fs = Ma ..... (i) ∴ Acceleration of Block B,
∴ Acceleration of Block B,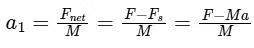
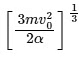
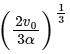
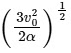
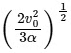
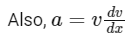
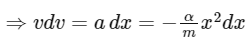
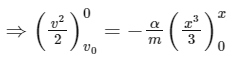
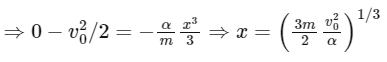

 On smooth incline
On smooth incline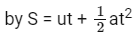
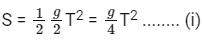
 For rough surface,
For rough surface,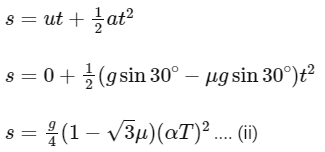
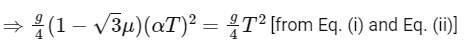
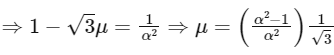
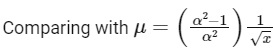
 Here, F' is the pseudo force acting on the bob when we considered it from car's frame and T is the tension on the string.
Here, F' is the pseudo force acting on the bob when we considered it from car's frame and T is the tension on the string.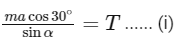
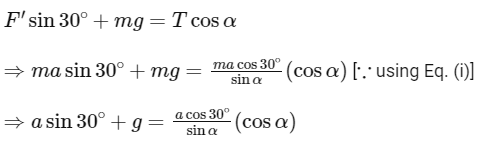
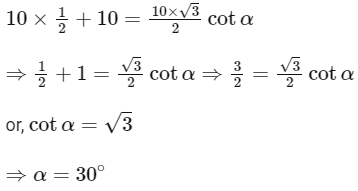
 Ans: 15
Ans: 15 fsmax = 1a (for 1 kg block) ............ (ii)
fsmax = 1a (for 1 kg block) ............ (ii)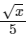 if the time of ascent is half of the time of descent. The value of x is __________.
if the time of ascent is half of the time of descent. The value of x is __________.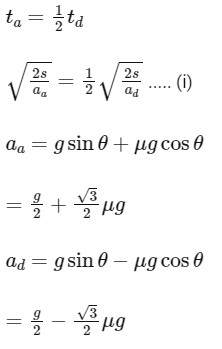
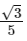

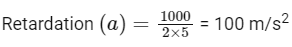
 Ans: 30
Ans: 30 ∵ f = T
∵ f = T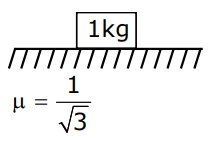 Minimum possible force ⇒
Minimum possible force ⇒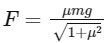
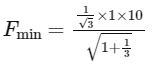
 Ans:
Ans:
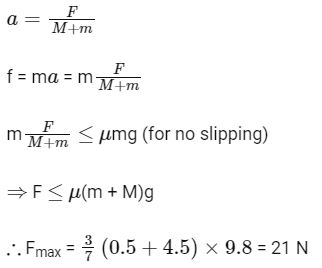
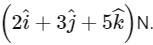 It starts from rest and was at the origin initially. After 4s, its new coordinates are (8, b, 20). The value of b is _____________. (Round off to the Nearest Integer)
It starts from rest and was at the origin initially. After 4s, its new coordinates are (8, b, 20). The value of b is _____________. (Round off to the Nearest Integer)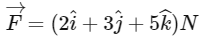
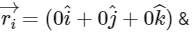 u (initial velocity) = 0
u (initial velocity) = 0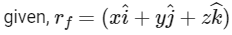
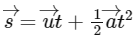
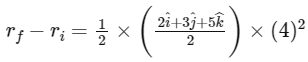

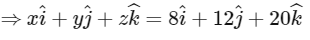
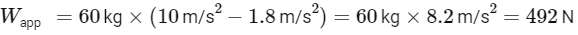
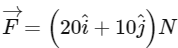 on a frictionless surface. If the box was initially at rest, then ___________ m is displacement along the x-axis after 10s.
on a frictionless surface. If the box was initially at rest, then ___________ m is displacement along the x-axis after 10s.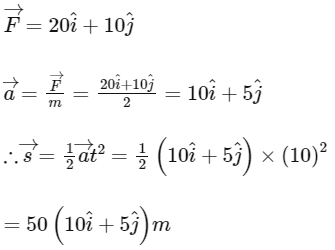
 The critical force to be applied on the vertical surface as shown at an angle 60∘ with horizontal such that it does not move, will be 3x. The value of x will be _________.
The critical force to be applied on the vertical surface as shown at an angle 60∘ with horizontal such that it does not move, will be 3x. The value of x will be _________.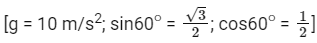
 Ans: 3.33
Ans: 3.33
 N = Mg + Fsin60∘
N = Mg + Fsin60∘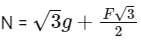
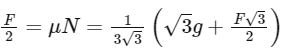
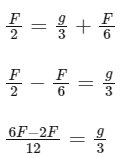
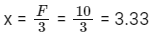
 At maximum height, the slope of tangent drawn,
At maximum height, the slope of tangent drawn,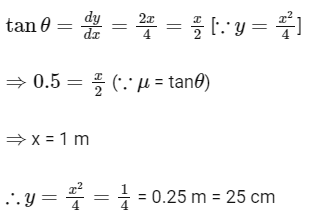
 Various forces acting on block are shown below
Various forces acting on block are shown below Frictional force ≤ mg
Frictional force ≤ mg 
























