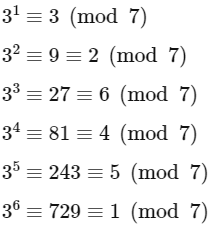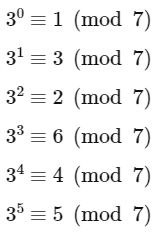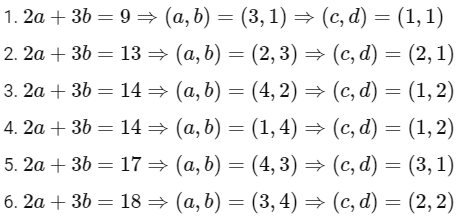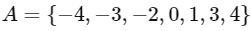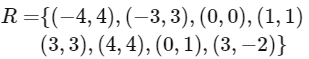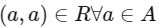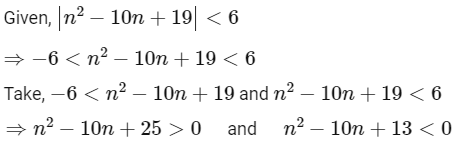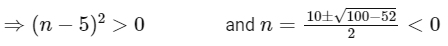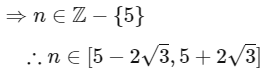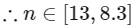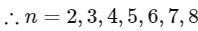[JEE Mains MCQs]
Q1: Let A = {1 , 3 , 4 , 6 , 9} and B = {2 , 4 , 5 , 8 , 10}. Let R be a relation defined on A × B such that R = {((a1, b1) , (a2 , b2)) : a1 ≤ b2 and b1 ≤ a2}. Then the number of elements in the set R is:
(a) 180
(b) 26
(c) 52
(d) 160
Ans: (d)
Given that the sets are A = {1, 3, 4, 6, 9} and B = {2, 4, 5, 8, 10}, for the relation R on the set A × B, we need to find the combinations of pairs that satisfy the conditions a1 ≤ b2 and b1 ≤ a2.
We find the number of combinations by considering the possible values for b2 for each a1 and the possible values for a2 for each b1:
For each a1 in A = {1, 3, 4, 6, 9} , the number of valid b2 values in B = {2, 4, 5, 8, 10} are:
- For a1 = 1 , there are 5 choices for b2.
- For a1 = 3 , there are 4 choices for b2.
- For a1 = 4 , there are 4 choices for b2.
- For a1 = 6 , there are 2 choices for b2.
-For a1 = 9 , there is 1 choice for b2.
This results in a total of 5 + 4 + 4 + 2 + 1 = 16 possible pairs (a1 , b2).
Similarly, for each b1 in B, the number of valid a2 values in A are:
- For b1 = 2 , there are 4 choices for a2.
- For b1 = 4 , there are 3 choices for a2.
- For b1 = 5 , there are 2 choices for a2.
- For b1 = 8 , there is 1 choice for a2.
- For b1 = 10 , there are no choices for a2.
This results in a total of 4 + 3 + 2 + 1 + 0 = 10 possible pairs (b1 , a2).
Therefore, the total number of elements in the relation R , which satisfies the given conditions, is 16 × 10 = 160.
So, the correct answer is 160.
Q2: An organization awarded 48 medals in event 'A', 25 in event 'B' and 18 in event 'C'. If these medals went to total 60 men and only five men got medals in all the three events, then, how many received medals in exactly two of three events?
(a) 10
(b) 15
(c) 21
(d) 9
Ans: (c)
We are given the number of medals for events A, B, and C which are 48, 25, and 18 respectively. We are also given that the total number of unique medal recipients across all events is 60 and that 5 people received a medal in all three events.
Using the Principle of Inclusion and Exclusion (PIE), we know that the total number of unique medal recipients can be calculated by adding the number of medal recipients in each event, subtracting the number of people who received a medal in any two events (to correct for double counting), and then adding back the number of people who received a medal in all three events (since we subtracted these people too much).
Mathematically, this can be represented as:
|A ∪ B ∪ C| = |A| + |B| + |C| - |A ∩ B| - |B ∩ C| - |C ∩ A| + |A ∩ B ∩ C|
However, we want to find the total number of people who received a medal in any two events (which is represented by |A ∩ B| + |B ∩ C| + |C ∩ A| in the equation).
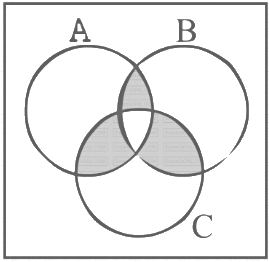 To find this, we rearrange the PIE formula to solve for |A ∩ B| + |B ∩ C| + |C ∩ A|:
To find this, we rearrange the PIE formula to solve for |A ∩ B| + |B ∩ C| + |C ∩ A|:
|A ∩ B| + |B ∩ C| + |C ∩ A| = |A| + |B| + |C| + |A ∩ B ∩ C| - |A ∪ B ∪ C|
Substituting the given values, we find that the total number of people who received a medal in any two events is 48 + 25 + 18 + 5 - 60 = 36.
However, this includes people who received a medal in all three events, and we want to find the number of people who received a medal in exactly two events. Therefore, we need to subtract the people who received a medal in all three events from our calculated value.
Since each person who received a medal in all three events is counted three times in |A ∩ B| + |B ∩ C| + |C ∩ A| (once for each pair of events), we subtract three times the number of people who received a medal in all three events from our calculated value:
Number of people who received a medal in exactly two events = |A ∩ B| + |B ∩ C| + |C ∩ A| - 3 × |A ∩ B ∩ C|
Substituting the values we know, we find that the number of people who received a medal in exactly two events is 36 - 3 × 5 = 21.
Therefore, 21 people received a medal in exactly two of the three events.
Q3: Let A = {2, 3, 4} and B = {8, 9, 12}. Then the number of elements in the relation R = {((a1 , b1) , (a2 , b2)) ∈ (A × B , A × B) : a1 divides b2 and a2 divides b1} is :
(a) 18
(b) 24
(c) 36
(d) 12
Ans: (c)
Given sets:
A = 2,3,4
B = 8,9,12
We want to find the number of elements of the form ((a1, a1), (b2, b2)) such that:
a1 divides b2
a2 divides b1
For the first condition:
a1 divides b2
Given a1∈ A and b2 ∈ B, we can list the pairs:
(a1, b2)∈(2, 8),(2, 12),(3, 9),(3, 12),(4, 8),(4, 12)
This gives 6 pairs.
For the second condition, the pairs are the same, because it's just the reversed relation. So:
a2 divides b1
Again has 6 valid pairs.
Now, for every pair from the first condition, we can have any pair from the second condition. This leads to: 6 × 6 = 36 relations.
Q4: Let A = {1, 2, 3, 4, 5, 6, 7}. Then the relation R = {(x, y) ∈ A × A : x + y = 7} is:
(a) reflexive but neither symmetric nor transitive
(b) transitive but neither symmetric nor reflexive
(c) symmetric but neither reflexive nor transitive
(d) an equivalence relation
Ans: (c)
Here, A = {1, 2, 3, 4, 5, 6, 7}
Since, x + y = 7 ⇒ y = 7 − x
So, R = {(1, 6) (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)}
∵ (a, b) ∈ R ⇒ (b, a) ∈ R
∴ R is symmetric only.
Q5: Let P(S) denote the power set of S = {1, 2, 3, … ., 10}. Define the relations R1 and R2 on P(S) as AR1 B if (A∩Bc) ∪ (B ∩ Ac) = ∅ and AR2 B if A ∪ Bc = B ∪ Ac , ∀ A , B ∈ P (S). Then:
(a) only R2 is an equivalence relation
(b) both R1 and R2 are not equivalence relations
(c) both R1 and R2 are equivalence relations
(d) only R1 is an equivalence relation
Ans: (c)
S = {1, 2, 3, .... 10}
P(S) = power set of S
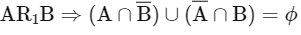
R1 is reflexive, symmetric
For transitive
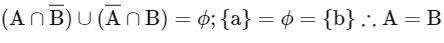
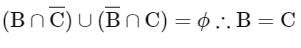
∴ A = C equivalence.
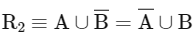
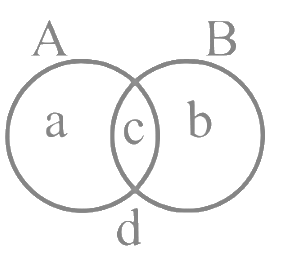
R2 → Reflexive, symmetric
For transitive:
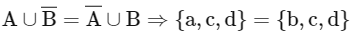
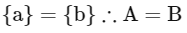
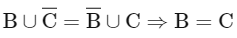
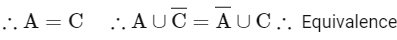
Q6: Let R be a relation on 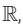 given by � = {(a, b) : 3a − 3b + 7 is an irrational number}. Then R is
given by � = {(a, b) : 3a − 3b + 7 is an irrational number}. Then R is
(a) an equivalence relation
(b) reflexive and symmetric but not transitive
(c) reflexive and transitive but not symmetric
(d) reflexive but neither symmetric nor transitive
Ans: (d)
For reflexive:
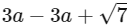

For transitive :
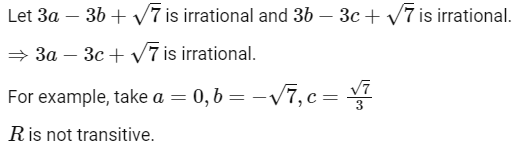
Q7: Among the relations
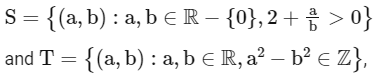
(a) S is transitive but T is not
(b) both S and T are symmetric
(c) neither S nor T is transitive
(d) T is symmetric but S is not
Ans: (d)
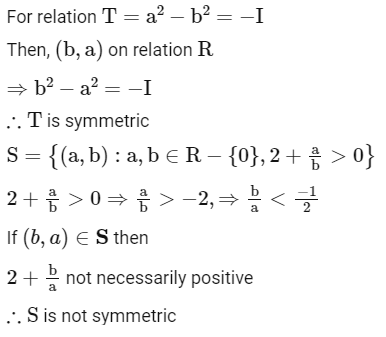
Q8: Let R be a relation on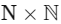 defined by (a , b) R (c , d) if and only if ab(b − c) = bc (a − d). Then R is
defined by (a , b) R (c , d) if and only if ab(b − c) = bc (a − d). Then R is
(a) symmetric and transitive but not reflexive
(b) reflexive and symmetric but not transitive
(c) transitive but neither reflexive nor symmetric
(d) symmetric but neither reflexive nor transitive
Ans: (d)
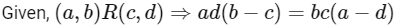
Symmetric:
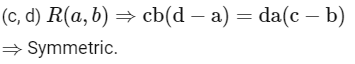
Reflexive:
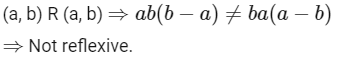
Transitive:
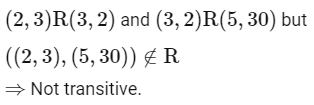
Q9: The minimum number of elements that must be added to the relation R = {(a, b) , (b, c)} on the set {a , b, c} so that it becomes symmetric and transitive is :
(a) 7
(b) 3
(c) 4
(d) 5
Ans: (a)

7 elements must be added
Q10: Let R be a relation defined on 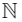 as aRb if 2a+ 3b is a multiple of 5 , a , b ∈
as aRb if 2a+ 3b is a multiple of 5 , a , b ∈ 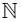 . Then R is
. Then R is
(a) an equivalence relation
(b) non reflexive
(c) symmetric but not transitive
(d) transitive but not symmetric
Ans: (a)
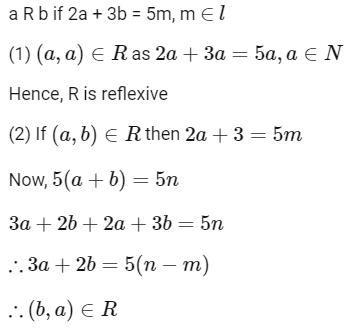
∴ R is symmetric
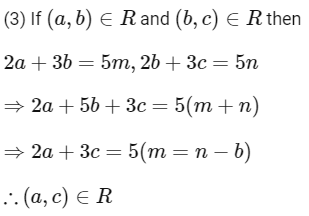
∴ R is transitive
Hence, R is equivalence relation.
Option (1) is correct.
Q11: The relation R = {(a, b) : gcd (a, b) = 1, 2 a ≠ b , a , b ∈ 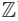 } is:
} is:
(a) reflexive but not symmetric
(b) transitive but not reflexive
(c) symmetric but not transitive
(d) neither symmetric nor transitive
Ans: (d)
Given, (a, b) belongs to relation R if gcd (a , b) = 1 , 2a ≠ b.
Here gcd means greatest common divisor. gcd of two numbers is the largest number that divides both of them.
(1) For Reflexive,
In aRa , gcd (a , a) = a
∴ This relation is not reflexive.
(2) For Symmetric:
Take a = 2 , b = 1 ⇒ gcd (2, 1) = 1 Also 2a = 4 ≠ b
Now gcd (b , a) = 1 ⇒ gcd (1, 2) = 1
and 2b should not be equal to a
But here, 2b = 2 = a
⇒ R is not Symmetric
(3) For Transitive: Let a = 14 , b = 19 , c = 21
gcd (a, b) = 1 , 2a ≠ b
gcd (b , c) = 1 , 2b ≠ c
gcd (a , c) = 7 , 2a ≠ c
Hence not transitive
⇒ R is neither symmetric nor transitive.
[JEE Mains Numericals]
Q12: The number of elements in the set {n ∈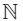 : 10 ≤ n ≤ 100 and 3n − 3 is a multiple of 7} is _____
: 10 ≤ n ≤ 100 and 3n − 3 is a multiple of 7} is _____
Ans: 15
To determine the number of elements in the given set, we need to find how many natural numbers n between 10 and 100 (inclusive) satisfy the condition that 3n − 3 is a multiple of 7.
Recall that for any integers a and b, a is a multiple of b if there exists an integer k such that a = bk. So in our case, we need to find how many n satisfy the equation 3n − 3 = 7k for some integer k.
Notice that 3n − 3 = 3 (3n−1 − 1). We want this expression to be a multiple of 7. Let's explore a few powers of 3 modulo 7:
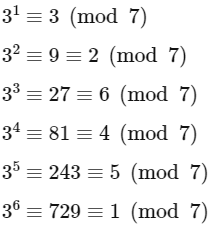
We observe that 3n (mod 7) follows a cycle of length 6. So, 3n − 1 (mod 7) also follows the same cycle, but shifted:
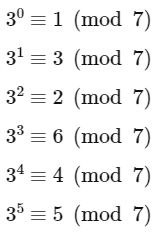
We want 3 (3n − 1 − 1) ≡ 0 (mod 7), which means that 3n − 1 − 1 ≡ 0 (mod 7). From the cycle above, we see that this is true when n − 1 is a multiple of 6, or equivalently, when n is one more than a multiple of 6.
Now let's find the multiples of 6 between 10 and 100:
12 , 18 , 24 , 30 , 36 , 42 , 48 , 54 , 60 , 66 , 72 , 78 , 84 , 90 , 96
Adding 1 to each of these values, we get the set of natural numbers n that satisfy the given condition:
13 , 19 , 25 , 31 , 37 , 43 , 49 , 55 , 61 , 67 , 73 , 79 , 85 , 91 , 97
There are 15 elements in this set. Therefore, the number of elements in the given set is 15.
Q13: Let A = {1, 2, 3, 4} and R be a relation on the set A × A defined by R = {((a, b), (c, d)): 2a + 3b = 4c + 5d}. Then the number of elements in R is ____________.
Ans: 6
2a + 3b = 4c + 5d
Given A = {1, 2, 3, 4}, the maximum value of 2a + 3b is 20, when (a, b) = (4, 4), and the minimum value of 4c + 5d is 9, when (c, d) = (1, 1). Therefore, the possible values for 2a + 3b = 4c + 5d are 9, 13, 14, 17, 18, and 19.
Now, let's find the combinations of (a, b), (c, d) that satisfy the given equation:
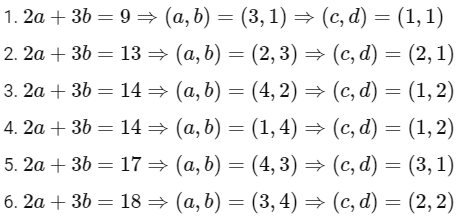
There are a total of 6 elements in the relation R for the given equation with the specified values of a, b, c, and d.
Q14: Let A = { − 4 , − 3 , − 2 , 0 , 1 , 3 , 4 } and R = {(a , b) ∈ A × A : b = | a | or b2 = a + 1} be a relation on A. Then the minimum number of elements, that must be added to the relation R so that it becomes reflexive and symmetric, is __________
Ans: 7
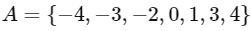
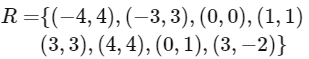
Relation to be reflexive 
⇒ (− 4 , − 4) , (− 3 , − 3) , (− 2 , − 2) also should be added in R.
Relation to be symmetric if (a , b) ∈ R, then (b , a) ∈ R ∀ a , b ∈ A
⇒ (4 , − 4) , (3, − 3) , (1 , 0) , (− 2 , 3) also should be added in R
⇒ Minimum number of elements to be added to R = 3 + 4 = 7
Q15: The number of relations, on the set {1 , 2 , 3} containing (1 , 2) and (2 , 3), which are reflexive and transitive but not symmetric, is __________.
Ans: 4
(1 , 1) , (2 , 2) , (3 , 3) ∈ R
Since (1 , 2) , (2, 3) ∈ R, (1 , 3) must ∈ R
Possible cases:
Case-1 : All of (2 , 1) , (3 , 2) , (3 , 1) ∉ R → 1 relation.
Case-2 : Only one of (2 , 1) , (3 , 2) , (3 , 1) ∈ R → 3 relations.
Note that exactly two of (2 , 1) , (3 , 2) , (3 , 1) ∈ R is not possible because if two of these ∈ R , third must ∈ R to make relation transitive.
1. R1 = {(1,1), (2,2), (3,3), (1,2), (2,3), (1,3)} Here, none of (2,1), (3,2), (3,1) are in R1.
2. R2 = {(1,1), (2,2), (3,3), (1,2), (2,3), (1,3), (2,1)} Here, only (2,1) is in R2, and neither (3,2) nor (3,1) are in R2.
3. R3 = {(1,1), (2,2), (3,3), (1,2), (2,3), (1,3), (3,2)} Here, only (3,2) is in R3, and neither (2,1) nor (3,1) are in R3.
4. R4 = {(1,1), (2,2), (3,3), (1,2), (2,3), (1,3), (3,1)} Here, only (3,1) is in R4, and neither (2,1) nor (3,2) are in R4.
Q16: The number of elements in the set {n ∈ Z : | n2 − 10n + 19 | < 6} is _________.
Ans: 6
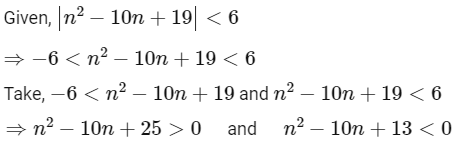
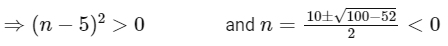
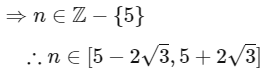
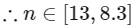
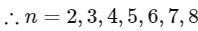
Thus, number of element in the set is '6'
Q17: Let A = { 0 , 3 , 4 , 6 , 7 , 8 , 9 , 10 } and R be the relation defined on A such that R = {(x , y) ∈ A × A : x − y is odd positive integer or x − y = 2}. The minimum number of elements that must be added to the relation R, so that it is a symmetric relation, is equal to ____________.
Ans: 19
We have, A = {0 , 3 , 4 , 6 , 7 , 8 , 9 , 10}
Case I: x − y is odd, if one is odd and one is even and x > y.
∴ Possibilites are {(3 , 0) , (4 , 3) , (6 , 3) , (7 , 6) , (7 , 4) , (7 , 0) , (8 , 7) , (8 , 3) , (9 , 8) , (9 , 6) , (9 , 4) , (9 , 0) , (10 , 9) , (10 , 7) , (10 , 3)}
No. of cases = 15
Case II: x − y = 2
∴ Possibilities are {(6 , 4) , (8 , 6) , (9 , 7) , (10 , 8)}
∴ No. of cases = 4
So, minimum ordered pair to be added = 15 + 4 = 19
Q18: Let A = {1, 2, 3, 4 , … . , 10} and B = {0 , 1 , 2 , 3 , 4}. The number of elements in the relation R = {(a , b) ∈ A × A : 2 (a − b)2 + 3 (a − b) ∈ B} is ___________.
Ans: 18
Given sets : A={1, 2, 3, 4, ............,10}
B = {0, 1, 2, 3, 4}
We are looking for pairs (a , b) ∈ A × A such that :
2 (a - b)2 + 3 (a - b) ∈ B
Let's break down the relation :
Case 1: a − b = 0
2(a - b)2 + 3 (a - b) = 0
Pairs : (1 , 1) , (2 , 2) , (3 , 3) , … , ( 10 , 10 ) which gives 10 pairs.
Case 2 : a − b = 1
2(a - b)2 + 3 (a - b) = 2 (1) + 3 (1) = 5
But 5 is not in B, so no pairs for this case.
Case 3 : a − b = − 1
2(a - b)2 + 3 (a - b) = 2 (1) − 3 (1) = − 1
This value is not in B, so no pairs for this case.
Case 4 : a − b = 2
2(a - b)2 + 3 (a - b) = 2(4) + 3 (2) = 8 + 6 = 14
Again, 14 is not in B, so no pairs for this case.
Case 5: a − b = − 2
2(a - b)2 + 3 (a - b) = 2(4) − 3(2) = 8 − 6 = 2
Pairs : (1 , 3) , (2, 4), (3 , 5) , (4 , 6) , (5 , 7) , (6 , 8) , (7 , 9) , (8 , 10) which gives 8 pairs.
For any other a − b value, the quadratic will grow larger than the maximum value in B, so we don't need to consider them.
In total, we have 10 + 8 = 18 pairs in the relation R.
Therefore, the number of elements in the relation R is 18.
Q19: Let S = {1, 2, 3, 5, 7, 10, 11}. The number of non-empty subsets of S that have the sum of all elements a multiple of 3, is _____________.
Ans: 43
Elements of the type 3k = 3
Elements of the type 3k + 1 = 1 , 7 , 9
Elements of the type 3k + 2 = 2 , 5 , 11
Subsets containing one element S1 = 1
Subsets containing two elements
S2 = 3C 1 × 3C1 = 9
Subsets containing three elements
S3 = 3C1 × 3C1 + 1 + 1 = 11
Subsets containing four elements
S4 = 3C3 + 3C3 + 3C2 × 3C2 = 11
Subsets containing five elements
S5 = 3C2 × 3C2 × 1 = 9
Subsets containing six elements
S6 = 1
Subsets containing seven elements S7 = 1
⇒ sum = 43
Q20: The minimum number of elements that must be added to the relation R = {(a, b), (b, c), (b, d)} on the set {a, b, c, d} so that it is an equivalence relation, is __________.
Ans: 13
R = { (a , b) (b , c) (b , d)}
S : {a , b , c , d}
Adding (a , a) , (b , b) , (c , c) , (d , d) make reflexive.
Adding (b , a) , (c , b) , (d , b) make Symmetric
And adding (a , d) , (a , c) to make transitive
Further (d , a) & (c , a) to be added to make Symmetricity.
Further (c , d) & (d , c) also be added.
So total 13 elements to be added to make equivalence.
 To find this, we rearrange the PIE formula to solve for |A ∩ B| + |B ∩ C| + |C ∩ A|:
To find this, we rearrange the PIE formula to solve for |A ∩ B| + |B ∩ C| + |C ∩ A|: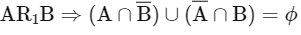
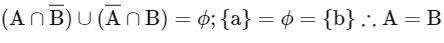
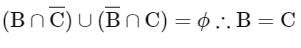

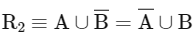

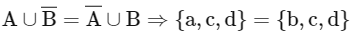
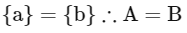
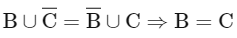
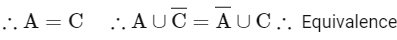
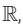 given by � = {(a, b) : 3a − 3b + 7 is an irrational number}. Then R is
given by � = {(a, b) : 3a − 3b + 7 is an irrational number}. Then R is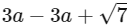

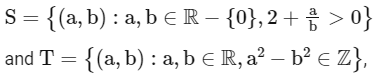
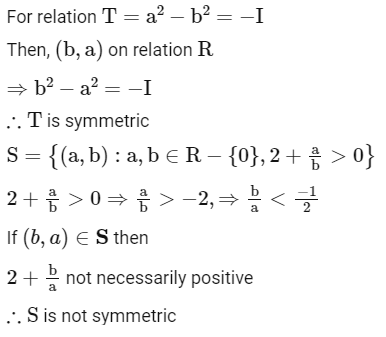
 defined by (a , b) R (c , d) if and only if ab(b − c) = bc (a − d). Then R is
defined by (a , b) R (c , d) if and only if ab(b − c) = bc (a − d). Then R is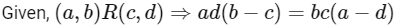
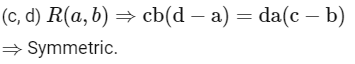
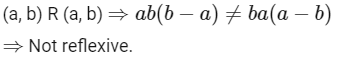
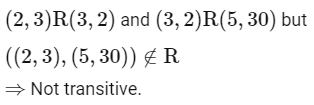

 as aRb if 2a+ 3b is a multiple of 5 , a , b ∈
as aRb if 2a+ 3b is a multiple of 5 , a , b ∈ 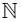 . Then R is
. Then R is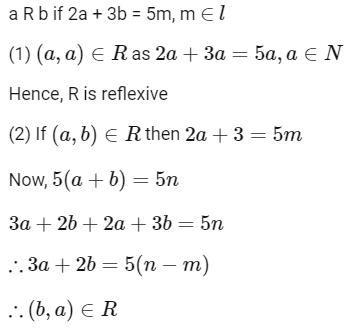
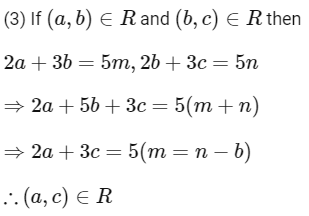
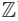 } is:
} is: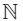 : 10 ≤ n ≤ 100 and 3n − 3 is a multiple of 7} is _____
: 10 ≤ n ≤ 100 and 3n − 3 is a multiple of 7} is _____