JEE Main Previous Year Questions (2025): Sets and Relations | Chapter-wise Tests for JEE Main & Advanced PDF Download
[JEE Mains MCQs]
Q1: Let R be a relation from the set {1 , 2, 3, … , 60} to itself such that R = {(a , b) : b = pq, where p , q ⩾ 3 are prime numbers}. Then, the number of elements in R is :
(a) 600
(b) 660
(c) 540
(d) 720
Ans: (b)
We have a set S = {1, 2, 3, ..., 60}, and a relation R defined on the set S. An element (a, b) belongs to the relation R if and only if b can be expressed as the product of two prime numbers p and q, where both p and q are greater than or equal to 3.
In terms of number theory, prime numbers are integers greater than 1 that have no divisors other than 1 and themselves. We are interested in prime numbers that are greater than or equal to 3, because p and q must both be greater than or equal to 3.
The primes greater than or equal to 3 and less than or equal to 60 are {3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59}.
We need to find all possible values of b = p × q such that b belongs to the set S. We start by choosing the smallest prime number (which is 3) and keep multiplying it with all the prime numbers until the product exceeds 60:
1. If we start with p = 3, we can choose q to be 3, 5, 7, 11, 13, 17, or 19. This gives us 7 valid products that are less than or equal to 60.
2. If we start with p = 5, we can choose q to be 5, 7, or 11. This gives us 3 valid products that are less than or equal to 60.
3. If we start with p = 7, we can choose q to be 7. This gives us 1 valid product that is less than or equal to 60.
So, we have a total of 7 + 3 + 1 = 11 possible values for b = p × q that satisfy the conditions.
Since a can be any number in the set S, there are 60 possible values for a for each of the 11 values of b. Therefore, the total number of elements in the relation R is 60 × 11 = 660.
Q2: For α ∈ N , consider a relation R on N given by R = {(x , y) : 3x + αy is a multiple of 7}. The relation R is an equivalence relation if and only if :
(a) α = 14
(b) α is a multiple of 4
(c) 4 is the remainder when α is divided by 10
(d) 4 is the remainder when α is divided by 7
Ans: (d)
R = {(x, y) : 3x + αy is multiple of 7}, now R to be an equivalence relation
(1) R should be reflexive: 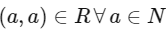
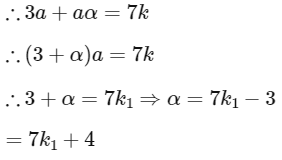
(2) R should be symmetric: 
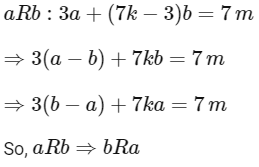
∴ R will be symmetric for a = 7k1 - 3
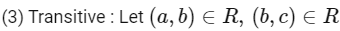
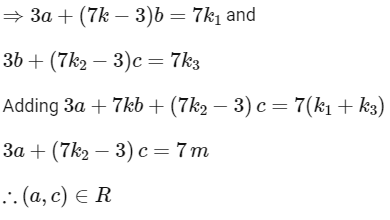
∴ R is transitive
∴ 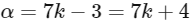
Q3: Let R1 and R2 be two relations defined on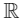 by a R1 b ⇔ ab ≥ 0 and a R2 b ⇔ a ≥ b
by a R1 b ⇔ ab ≥ 0 and a R2 b ⇔ a ≥ b
Then,
(a) R 1 is an equivalence relation but not R2
(b) R2 is an equivalence relation but not R1
(c) both R1 and R2 are equivalence relations
(d) neither R1 nor R2 is an equivalence relation
Ans: (d)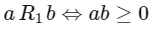

⇒ Then (a , c) may or may not belong to R1
{Consider a = − 5, b = 0 , c = 5 so (a , b) and (b , c) ∈ R1 but ac < 0}
So, R1 is not equivalence relation
a R2b ⇔ a ≥ b
(a , a) ∈ R2 ⇒ so reflexive relation
If (a , b) ∈ R2 then (b , a) may or may not belong to R2
⇒ So not symmetric Hence it is not equivalence relation
Q4: Let a set A = A1 ∪ A2 ∪ ..... ∪ Ak, where Ai ∩ Aj = ϕ for i ≠ j, 1 ≤ j, j ≤ k. Define the relation R from A to A by R = {(x, y) : y ∈ Ai if and only if x ∈ Ai, 1 ≤ i ≤ k}. Then, R is :
(a) reflexive, symmetric but not transitive.
(b) reflexive, transitive but not symmetric.
(c) reflexive but not symmetric and transitive.
(d) an equivalence relation.
Ans: (d)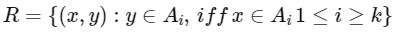
(1) Reflexive
Q5: Let R1 = {(a, b) ∈ N × N : |a − b| ≤ 13} and
R2 = {(a, b) ∈ N × N : |a − b| ≠ 13}. Then on N :
(a) Both R1 and R2 are equivalence relations
(b) Neither R1 nor R2 is an equivalence relation
(c) R1 is an equivalence relation but R2 is not
(d) R2 is an equivalence relation but R1 is not
Ans: (b)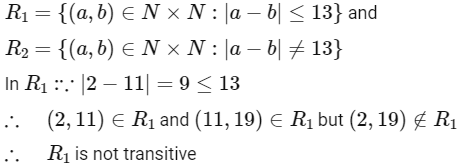
Hence R1 is not equivalence
In R2 : (13 , 3) ∈ R2 and (3 , 26) ∈ R2 but (13 , 26) ∉ R2 (∵ |13 − 26| = 13)
∴ R2 is not transitive
Hence R2 is not equivalence.
[JEE Mains Numericals]
Q6: Let S = {4 , 6 , 9} and T = {9 , 10 , 11 , … , 1000 }. If A = {a1 + a2 + … + ... ak : k ∈ N , a1 , a2 , a3 , … , 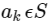 }, then the sum of all the elements in the set T − A is equal to __________.
}, then the sum of all the elements in the set T − A is equal to __________.
Ans: 11
Here S = {4 , 6 , 9}
And T = {9 , 10 , 11 , . . . . . . , 1000}.
We have to find all numbers in the form of 4x + 6y + 9z , where x , y , z ∈ { 0 , 1 , 2 , . . . . . . }.
If a and b are coprime number then the least number from which all the number more than or equal to it can be express as ax + by where x , y ∈ {0 , 1 , 2 , . . . . . . } is (a − 1) . (b − 1).
Then for 6y + 9z = 3 (2y + 3 z)
All the number from (2 − 1). (3 − 1) = 2 and above can be express as 2x + 3z (say t).
Now 4x+ 6y + 9z = 4x + 3 (t + 2)
= 4x + 3t + 6
again by same rule 4x + 3t, all the number from (4 − 1) (3 − 1) = 6 and above can be express from 4x + 3t.
Then 4x + 6y + 9z express all the numbers from 12 and above.
again 9 and 10 can be express in form 4x + 6y + 9z.
Then set A = {9 , 10 , 12 , 13 , . . . . , 1000} .
Then T − A = {11}
Only one element 11 is there.
Sum of elements of T - A = 11
Q7: Let A = {1 , 2 , 3 , 4 , 5 , 6 , 7} and B = {3 , 6 , 7 , 9}. Then the number of elements in the set {C ⊆ A : C ∩ B ≠ ϕ} is ___________.
Ans: 112
As C ∩ B ≠ ϕ , c must be not be formed by {1, 2, 4, 5}
∴ Number of subsets of A = 27 = 128 and number of subsets formed by {1, 2, 4, 5} = 16
∴ Required no. of subsets = 27 − 24 = 128 − 16 = 112
Q8: Let A = {1 , 2 , 3 , 4 , 5 , 6 , 7}. Define B = {T ⊆ A : either 1 ∉ T or 2 ∈ T} and C = {T ⊆ A : T the sum of all the elements of T is a prime number} . Then the number of elements in the set B ∪ C is ________________.
Ans: 107
∵ (B ∪ C)' = B' ∩C'
B' is a set containing sub sets of A containing element 1 and not containing 2.
And C' is a set containing subsets of A whose sum of elements is not prime.
So, we need to calculate number of subsets of {3, 4, 5, 6, 7} whose sum of elements plus 1 is composite. Number of such 5 elements subset = 1
Number of such 4 elements subset = 3 (except selecting 3 or 7)
Number of such 3 elements subset = 6 (except selecting {3, 4, 5}, {3, 6, 7}, {4, 5, 7} or {5, 6, 7})
Number of such 2 elements subset = 7 (except selecting {3, 7}, {4, 6}, {5, 7})
Number of such 1 elements subset = 3 (except selecting {4} or {6})
Number of such 0 elements subset = 1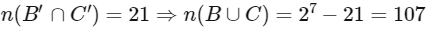
Q9: Let R1 and R2 be relations on the set {1, 2, ......., 50} such that
R1 = {(p, pn) : p is a prime and n ≥ 0 is an integer} and
R2 = {(p, pn) : p is a prime and n = 0 or 1}.
Then, the number of elements in R1 − R2 is _______________.
Ans: 8
Given, R1 = {(p , pn) : p is a Prime and n ≥ 0 is an integer}
and, set A = {1 , 2, 3 … … .50}
p is a Prime number which can take 15 values
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 and 47
∴ We can calculate no. of elements in R1
R1 = (2, 20) , (2, 21), (2, 22) (2, 23) … … (2, 25) = 6 number of ordered pairs
(3, 30) , (3 , 31) , (3, 32) …….. (3, 33) = 4 number of order paris
(5, 50) , (5, 51) , (5, 52) ……….. = 3 number of order paris
(7, 70) ……. (7, 72) ……… = 3 number of order paris
(11 , 110) and (11 , 111) = 2 number of order paris
(13 , 130) and (13 , 13 1) = 2 number of order paris
∴ For the 11 prime numbers (11 , 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 , 43 and 47), n can only be 0, 1 (two pairs each).
∴ n(R1) = 6 + 4 + 3 + 3 + (2 × 11) = 38
R2 = (p , pn), where n = 0 or 1
(2 , 20) , (2, 21) (3, 30) (3, 31) ….. (47 , 470) (47 , 471)
Two ordered pairs of each element n (R2) = 2 × 15 = 30 elements
Hence R1 - R2 = 38 - 30 = 8
Q10: Let A = {n ∈ N : H.C.F. (n, 45) = 1} and
Let B = {2k : k ∈ {1, 2, ......., 100}}. Then the sum of all the elements of A ∩ B is ____________.
Ans: 5264
Sum of all elements of A ∩ B = 2 [Sum of natural numbers upto 100 which are neither divisible by 3 nor by 5]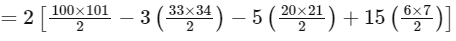
= 10100 - 3366 - 2100 + 630
= 5264
Q11: 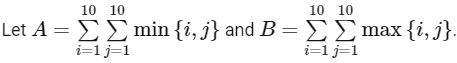
Then A + B is equal to _____________.
Ans: 1100
= minimum between i and j in all sets and summation of all those values.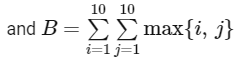
= maximum between i and j in all sets and summation of all those values.
For 1 :
1 is minimum in sets = {1, 1}, {1, 2}, {1, 3}, {1, 4}, {1, 5}, {1, 6}, {1, 7}, {1, 8}, {1, 9}, {1, 10}, {2, 1}, {3, 1}, {4, 1}, {5, 1}, {6, 1}, {7, 1}, {8, 1}, {9, 1}, {10, 1}
∴ 1 is minimum in 19 sets
1 is maximum in {1, 1} sets.
∴ 1 is maximum and minimum in total 20 sets.
∴ Sum of 1 in all those sets = 1 × 20 = 20
For 2 :
2 is minimum in sets = {2, 2}, {2, 3}, {2, 4}, {2, 5}, {2, 6}, {2, 7}, {2, 8}, {2, 9}, {2, 10}, {3, 2}, {4, 2}, {5, 2}, {6, 2}, {7, 2}, {8, 2}, {9, 2}, {10, 2} ∴ 2 is minimum in 17 sets
2 is maximum in sets = {1, 2}, {2, 1}, {2, 2}
∴ 2 is maximum and minimum in 20 sets.
∴ Sum of 2 in all those sets = 2 × 20 = 40
Similarly 3 is maximum and minimum in 20 sets.
∴ Sum of 3 in all those sets = 20 × 3 = 60
⋮
Similarly, 10 is maximum and minimum in 20 sets.
∴ Sum of 10 in all those sets = 20 × 10 = 200
∴ A + B = 20 + 20 × 2 + 20 × 3 + ....... + 20 × 10
= 20(1 + 2 + 3 + ...... + 10)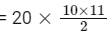
= 1100
Q12: The sum of all the elements of the set {α ∈ { 1 , 2 , . . . . . , 100 } : HCF (α , 24 ) = 1} is __________.
Ans: 1633
The numbers upto 24 which gives g.c.d. with 24 equals to 1 are 1, 5, 7, 11, 13, 17, 19 and 23. Sum of these numbers = 96
There are four such blocks and a number 97 is there upto 100.
∴ Complete sum
= 96 + (24 × 8 + 96) + (48 × 8 + 96) + (72 × 8 + 96) + 97
= 1633
|
481 docs|964 tests
|
















