JEE Main Previous Year Questions (2022): Permutations and Combinations | Chapter-wise Tests for JEE Main & Advanced PDF Download

[JEE Mains MCQs]

Q1: The number of ways to distribute 30 identical candies among four children C₁, C₂, C₃ and C₄ so that C₂ receives at least 4 and at most 7 candies, C₃ receives at least 2 and at most 6 candies, is equal to:
(a) 205
(b) 615
(c) 510
(d) 430
Ans: (d)
By multinomial theorem, no. of ways to distribute 30 identical candies among four children C₁, C₂ and C₃, C₄
= Coefficient of x³⁰ in (x⁴ + x⁵ + .... + x⁷) (x² + x³ + .... + x⁶) (1 + x + x² ....)²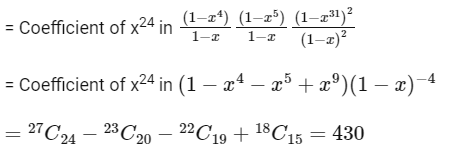


Q2: The total number of 5-digit numbers, formed by using the digits 1, 2, 3, 5, 6, 7 without repetition, which are multiple of 6, is :
(a) 36
(b) 48
(c) 60
(d) 72
Ans: (d)
To make a no. divisible by 3 we can use the digits 1,2,5,6,7 or 1,2,3,5,7.
Using 1,2,5,6,7, number of even numbers is = 4 × 3 × 2 × 1 × 2 = 48
Using 1,2,3,5,7, number of even numbers is = 4 × 3 × 2 × 1 × 1 = 24
Required answer is 72.

[JEE Mains Numericals]

Q3: The number of natural numbers lying between 1012 and 23421 that can be formed using the digits 2 , 3 , 4 , 5 , 6 (repetition of digits is not allowed) and divisible by 55 is _________.
Ans: 6
Case-I
When number is 4-digit number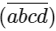here d is fixed as 5
So, (a , b , c) can be (6 , 4 , 3) , (3 , 4 , 6) , (2 , 3 , 6) , (6 , 3 , 2) , (3 , 2 , 4) or (4 , 2 ,  )
⇒ 6 numbers
Case-II 
No number possible

Q4:The number of matrices of order 3×3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is __________.
Ans: 282
In a 3 × 3 order matrix there are 9 entries.
These nine entries are zero or one.
The sum of positive prime entries are 2 , 3 , 5 or 7.
Total possible matrices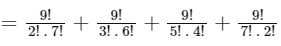
= 34 + 84 + 126 + 36
= 282

Q5: A class contains b boys and g girls. If the number of ways of selecting 3 boys and 2 girls from the class is 168 , then b + 3 g is equal to ____________.
Ans: 17

∴ b + 3g = 17

Q6: Let S be the set of all passwords which are six to eight characters long, where each character is either an alphabet from {A, B, C, D, E} or a number from {1, 2, 3, 4, 5} with the repetition of characters allowed. If the number of passwords in S whose at least one character is a number from {1, 2, 3, 4, 5} is α × 5⁶, then α is equal to ___________.
Ans: 7073
If password is 6 character long, then
Total number of ways having atleast one number =10⁶ − 5⁶
Similarly, if 7 character long = 10⁷ − 5⁷
and if 8-character long = 10⁸ − 5⁸
Number of password = (10⁶ + 10⁷ + 10⁸) − (5⁶ + 5⁷ + 5⁸)
= 5⁶(2⁶ + 5.2⁷ + 25.2⁸ − 1 − 5 − 25)
= 5⁶(64 + 640 + 6400 − 31)
= 7073 × 5⁶
∴ α = 7073.

Q7: Numbers are to be formed between 1000 and 3000 , which are divisible by 4 , using the digits 1, 2, 3, 4, 5 and 6 without repetition of digits. Then the total number of such numbers is ____________.
Ans: 30
Here 1st digit is 1 or 2 only
Case-I
If first digit is 1
Then last two digits can be 24, 32, 36, 52, 56, 64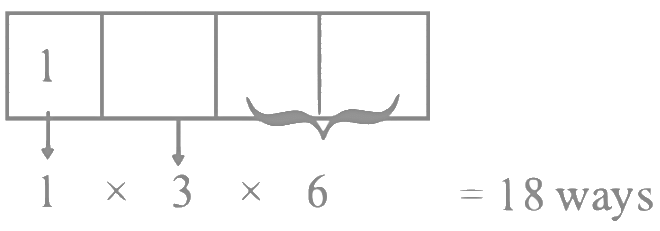

Case – II
If first digit is 2 then last two digit can be 16, 36, 56, 64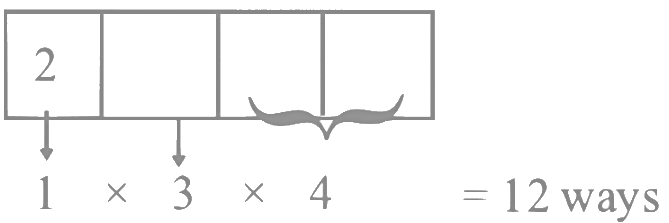
Total ways = 12 + 18 = 30 ways

Q8: The number of 5-digit natural numbers, such that the product of their digits is 36 , is __________.
Ans: 180
Factors of 36 = 2² . 3² . 1
Five-digit combinations can be
(1, 2, 2, 3, 3) (1, 4, 3, 3, 1), (1, 9, 2, 2, 1)
(1, 4, 9, 11) (1, 2, 3, 6, 1) (1, 6, 6, 1, 1)
i.e., total numbers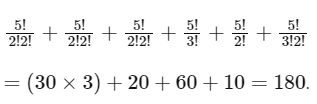


Q9: The letters of the word 'MANKIND' are written in all possible orders and arranged in serial order as in an English dictionary. Then the serial number of the word 'MANKIND' is _____________.
Ans: 1492
Step 1:
Write all the alphabets in alphabetical order.
Step 2:
Give a number to each alphabet starting from 0 in alphabetical order.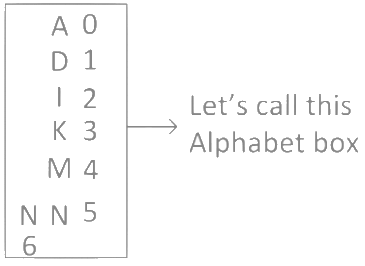
Step 3: 
In word "MANKIND" first alphabet is "M" which is present in the 4th position in the Alphabet Box. And after "M", in the word "MANKIND" there are 6 alphabets "ANKIND" which can be arrange in 6!/2! ways. Here 2! present because two N presents.
So for alphabet "M" we write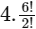  
Step 4: As in word "MANKIND" we calculated "M", so delete "M" from alphabet box and check remaining alphabets got right numbers or not in alphabet box.
As you can see after deleting "M", 4^th position in the alphabet box is missing so we create a new alphabet box.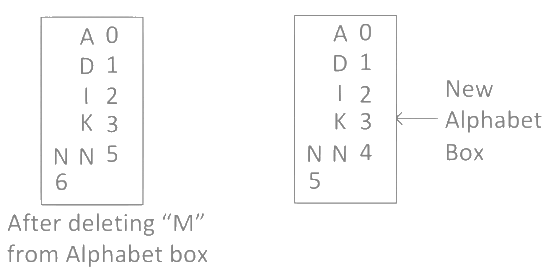
Step 5: Now next alphabet after "M" in word "MANKIND" is "A" which is present in the 0th position in the new alphabet box. And after "A" in the word "MANKIND" there are 5 alphabets "NKIND" which can be arrange in 5!/2! ways.
So, for alphabet "A" we write 0.5!/2!
Step 6: 
Now in word "MANKIND" we calculated "A", so delete "A" from previous new alphabet box and check remaining alphabets got right numbers or not in alphabet box.
As you can see after deleting "A", 0th positioin in the alphabet box is missing, so we have to create a new alphabet box.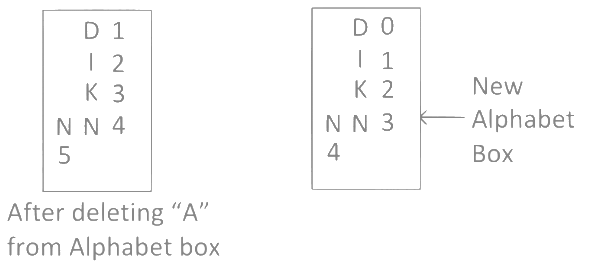
Step 7: Now next alphabet after "A" in word "MANKIND" is "N" which is present in the 3rd and 4th position in the alphabet box. We have to choose minimum position for "N" in the alphabet box. So, we choose 3rd position "N". And after "N" in the word "MANKIND" there are 4 alphabets "KIND" which can be arrange 4!/2! ways. Here 2! used because of 2 N's (one "N" is that "N" which we are considering and other "N" which is present in the word "KIND") 

So for alphabet "N" we write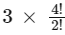
Step 8: Now in word "MANKIND" we calculated "N", so delete 3rd "N" from alphabet box and check remaining alphabets got right number or not in alphabet box. As you can see after deleting 3rd "N", 3rd position is missing in the alphabet box so we have to create a new alphabet box.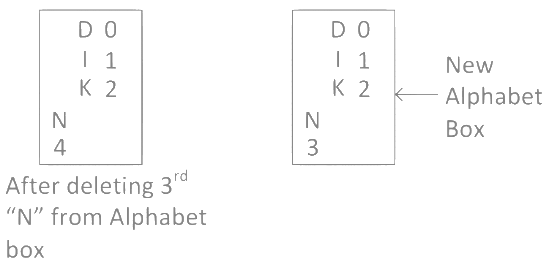

Step 9: Now next alphabet after "N" in word "MANKIND" is "K" which is present at the 2nd position in the new alphabet box. And after "K" in the word "MANKIND" there are 3 alphabets "IND" which we can arrange 3! ways.
So for alphabet "K" we write 2 × 3 !
Step 10: Now, in word "MANKIND" we calculated "K", so delete "K" from alphabet box and check remaining alphabets got right number or not in alphabet box. As you can see after deleting "K", 2nd position in the alphabet box is missing so we have to create a new alphabet box.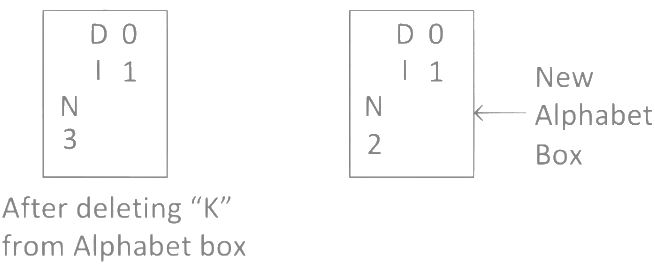
Step 11: 
Now next alphabet after "K" in word "MANKIND" is "I" which is present at 1st position in the new alphabet box. And after "I" in the word "MANKIND" there are 2 alphabets "ND" which we can arrange in 2 ! ways.
So for alphabet "I" we write 1 × 2! 

Step 12: Now in word "MANKIND" we calculated "I", so delete "I" from alphabet box and check remaining alphabets got right numbers or not in alphabet box. As you can see after deleting "I", 1st position in the alphabet box is missing so we have to create a new alphabet box.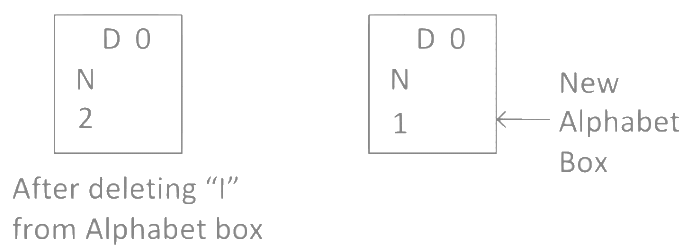

Step 13: Now next alphabet after "I" in word "MANKIND" is "N" which is present at 1st position in the new alphabet box. And after "N" in the word "MANKIND" there is 1 alphabet "D" which we can arrange in 1 ! ways.
So for alphabet "N" we write 1 × 1!.
Step 14: Now in word "MANKIND" we calculated "N", so delete "N" from alphabet box and check remaining alphabets got right numbering or not in alphabet box. As you can see after deleting "N", remaining alphabet "D" got correct numbering so new alphabet box will be same.

Step 15: 
Now next alphabet after "N" in word "MANKIND" is "D" which is present at the 0th position in the new alphabet box. And after "D" in the word "MANKIND" there is no alphabet so it is the last alphabet.
So for last alphabet we always write 0!
∴ Position of the word "MANKIND" in the dictionary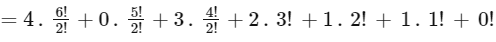


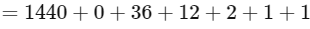
= 1492

Q10: The number of 6-digit numbers made by using the digits 1, 2, 3, 4, 5, 6, 7, without repetition and which are multiple of 15 is ____________.
Ans: 360
A number is multiple of 15 when the number is divisible by 5 and sum of digits of the number is divisible by 3.
Among 1, 2, 3, 4, 5, 6, 7 unit place is filled with 5 so it is multiple of 5.
Now to make it divisible by 3, take remaining 5 digits such a way that sum becomes divisible by 3. Remaining 5 digits can be
(1) 1, 2, 3, 4, 6
Here sum = 1 + 2 + 3 + 4 + 6 + 5 = 21 (divisible by 3)
This 5 digits can be filled in those 5 placed without repetition in 5 × 4 × 3 × 2 × 1 = 51 = 120 ways
(2) 2, 3, 4, 6, 7
Here sum = 2 + 3 + 4 + 6 + 7 + 5 = 27 (divisible by 3)
∴ Number of ways = 51 = 120
(3) 1, 2, 3, 6, 7
Here sum = 1 + 2 + 3 + 6 + 7 + 5 = 24 (divisible by 3)
∴ Number of ways = 51 = 120
∴ Total possible 6 digit numbers divisible by 15 = 120 + 120 + 120 = 360

Q11: The total number of four digit numbers such that each of first three digits is divisible by the last digit, is equal to ____________.
Ans: 1086
If unit digit is 1 then → 9 × s 10 × 10 = 900 numbers
If unit digit is 2 then → 4 × 5 × 5 = 100 numbers
If unit digit is 3 then → 3 × 4 × 4 = 48 numbers
If unit digit is 4 then → 2 × 3 × 3 = 18 numbers
If unit digit is 5 then → 1 × 2 × 2 = 4 numbers
If unit digit is 6 then → 1 × 2 × 2 = 4 numbers
For 7, 8, 9→ 4 + 4 + 4 = 12 Numbers
Total =1086 Numbers 

Q12: Let b₁b₂b₃b₄ be a 4-element permutation with bi ∈ {1, 2, 3, ........, 100} for 1 ≤ i ≤ 4 and b_i ≠ b_j for i ≠ j, such that either b₁, b₂, b₃ are consecutive integers or b₂, b₃, b₄ are consecutive integers. Then the number of such permutations b₁b₂b₃b₄ is equal to ____________.
Ans: 18915
There are 98 sets of three consecutive integer and 97 sets of four consecutive integers.
Using the principle of inclusion and exclusion,
Number of permutations of b₁b₂b₃b4_b = Number of permutations when b₁b₂b₃ are consecutive + Number of permutations when b₂b₃b₄ are consecutive - Number of permutations when b₁b₂b₃b₄ are consecutive
= 97 × 98 + 97 × 98 − 97 = 97 × 195 = 18915.

Q13: Let A be a matrix of order 2 × 2, whose entries are from the set {0, 1, 2, 3, 4, 5}. If the sum of all the entries of A is a prime number p, 2 < p < 8, then the number of such matrices A is ___________.
Ans: 180
∵ Sum of all entries of matrix A must be prime p such that 2 < p < 8 then sum of entries may be 3, 5 or 7. If sum is 3 then possible entries are (0, 0, 0, 3), (0, 0, 1, 2) or (0, 1, 1, 1).
∴ Total number of matrices
= 4 + 4 + 12 = 20
If sum of 5 then possible entries are (0, 0, 0, 5), (0, 0, 1, 4), (0, 0, 2, 3), (0, 1, 1, 3), (0, 1, 2, 2) and (1, 1, 1, 2).
∴ Total number of matrices
= 4 + 12 + 12 + 12 + 12 + 4 = 56
If sum is 7 then possible entries are (0, 0, 2, 5), (0, 0, 3, 4), (0, 1, 1, 5), (0, 3, 3, 1), (0, 2, 2, 3), (1, 1, 1, 4), (1, 2, 2, 2), (1, 1, 2, 3) and (0, 1, 2, 4).
Total number of matrices with sum 7 = 104
∴ Total number of required matrices
= 20 + 56 + 104
 = 180

Q14: The number of ways, 16 identical cubes, of which 11 are blue and rest are red, can be placed in a row so that between any two red cubes there should be at least 2 blue cubes, is _____________.
Ans: 56
First we arrange 5 red cubes in a row and assume x₁, x₂, x₃, x₄, x₅ and x₆ number of blue cubes between them
Here, x₁ + x₂ + x₃ + x₄ + x₅ + x₆ = 11 and x₂ , x₃ , x₄ , x₅ ≥ 2
So x₁ + x₂ + x₃ + x₄ + x₅ + x₆ = 3
No. of solutions = ⁸C₅ = 56

Q15: The total number of 3-digit numbers, whose greatest common divisor with 36 is 2, is ___________.
Ans: 150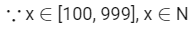


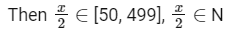
Number whose G.C.D. with 18 is 1 in this range have the required condition.
There are 6 such number from 18 × 3 to 18 × 4.
Similarly from 18 × 4 to 18 × 5 ......., 26 × 18 to 27 × 18
∴ Total numbers = 24 × 6 + 6 = 150
The extra numbers are 53, 487, 491, 493, 497 and 499.

Q16: There are ten boys B₁, B₂, ......., B₁₀ and five girls G₁, G₂, ........, G₅ in a class. Then the number of ways of forming a group consisting of three boys and three girls, if both B₁ and B₂ together should not be the members of a group, is ___________.
Ans: 4
Number of ways when B₁ and B₂ are not together
= Total number of ways of selecting 3 boys − B₁ and B₂ are together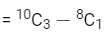


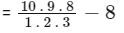
= 112
Number of ways to select 3 girls = ⁵C₃ = 10
∴ Total number of ways = 112 × 10 = 1120

Q17: The total number of three-digit numbers, with one digit repeated exactly two times, is ______________.
Ans: 243
C - 1 : All digits are non-zero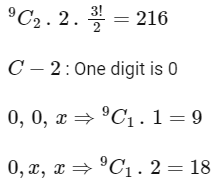

Total = 216 + 27 = 243

Q18: The number of 3-digit odd numbers, whose sum of digits is a multiple of 7, is _____________.
Ans: 63
For odd number unit place shall be 1 , 3 , 5 , 7 or 9.
∴ x y 1, x y 3, x y 5, x y 7, x y 9 are the type of numbers. numbers.
If xy 1 then x + y = 6 , 13 , 20 ... Cases are required
i.e., 6 + 6 + 0 + … = 12 ways
If xy 3 then
x + y = 4 , 11 , 18 , … Cases are required
i.e., 4 + 8 + 1 + 0 … = 13 ways
Similarly for xy 5 , we have x + y = 2 , 9 , 16 , …
i.e., 2 + 9 + 3 = 14 ways
for x y we have
x + y = 0 , 7 , 14 , …
i.e., 0 + 7 + 5 = 12 ways
And for x y we have
x + y = 5 , 12 , 19 …
i.e., 5 + 7 + 0 … = 12 ways
∴ Total 63 ways

Q19: Let A be a 3 × 3 matrix having entries from the set { − 1, 0, 1}. The number of all such matrices A having sum of all the entries equal to 5, is ___________.
Ans:
Case-I: 

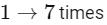
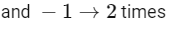
number of possible marrix = 9!/7!2! = 36
Case-II:
1→6 times,
−1→1 times
and 0 → 2 times
number of possible marrix =9!/6!2! = 252
Case-III:
1 → 5 times,
and 0 → 4 times
number of possible marrix = 9!/5!4!=126
Hence total number of all such matrix A = 414  

Q20: The number of 7-digit numbers which are multiples of 11 and are formed using all the digits 1, 2, 3, 4, 5, 7 and 9 is _____________.
Ans: 576
Digits are 1, 2, 3, 4, 5, 7, 9
Multiple of 11→ Difference of sum at even and odd place is divisible by 11 .
Let number of the form abcdefg
either or  
∴(a + c + e + g) − (b + d + f) = 11x
a + b + c + d + e + f = 31
∴ either a + c + e + g = 21 or 10
∴b + d + f = 10 or 21
Case-1
a + c + e + g = 21
b + d + f = 10
(b, d, f) ∈ {(1, 2, 7) (2, 3, 5) (1, 4, 5)}
(a, c, e, g)∈{(1, 4, 7, 9),(3, 4, 5, 9),(2, 3, 7, 9)}
Case-2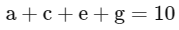




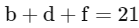
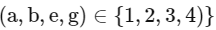
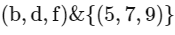
∴  Total number in case
∴ Total numbers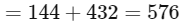

Q21: In an examination, there are 5 multiple choice questions with 3 choices, out of which exactly one is correct. There are 3 marks for each correct answer, −2 marks for each wrong answer and 0 mark if the question is not attempted. Then, the number of ways a student appearing in the examination gets 5 marks is ____________.
Ans: 40
Let student marks x correct answers and y incorrect. So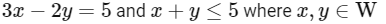

Only possible solution is (x , y) = (3 , 2)
Students can mark correct answers by only one choice but for an incorrect answer, there are two choices. So total number of ways of scoring 5 marks
= ⁵C₃(1)³. (2)² = 40