Cubes & Cube Roots Chapter Notes | Mathematics (Maths) Class 8 PDF Download

Introduction 

Ramanujan quickly corrected him, noting that 1729 is actually the smallest number expressible as the sum of two cubes in two different ways. 

• The cube of 10 plus the cube of 9: (10³ + 9³ = 1729)
• The cube of 12 plus the cube of 1: (12³ + 1³ = 1729)
  

This number, now known as the Hardy–Ramanujan Number, had been recognized long before, but Ramanujan's deep love for numbers led him to discover such fascinating properties.

Cubes

Word cube is used in geometry. It is a solid figure which all sides are equal.
Consider a cube of side 3 cm , How many cubes can be made of side 1cm from 3cm side cube!

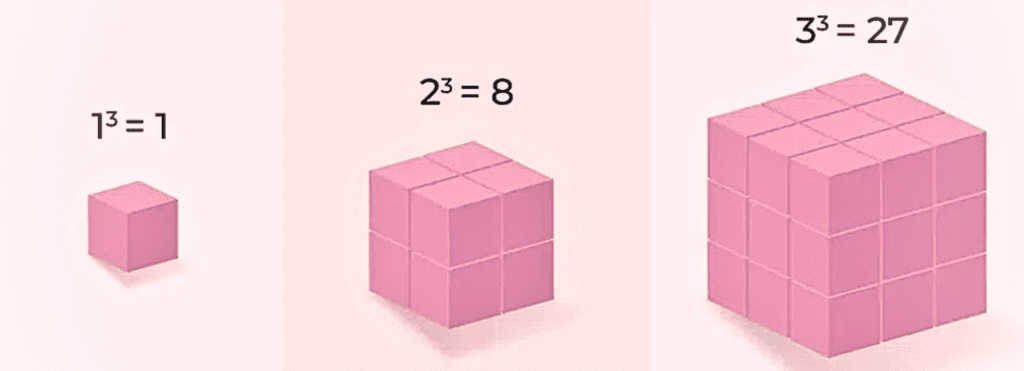
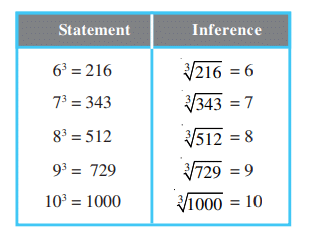
Cube of any number is obtained when the number is multiplied 3 times in a row.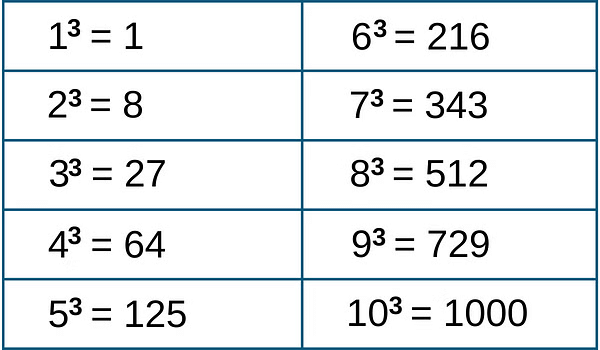Cubes till 10

Perfect Cube:  A perfect cube is a number that you get when you multiply a whole number by itself two more times.

A number of the form n³ where n is an integer.  

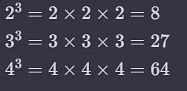
8, 27, 64 are perfect cubes.

There are only ten perfect cubes from 1 to 1000. Cube of any odd integer is odd and cube of any even integer is even.

Some Interesting Patterns

1.  Adding Consecutive Odd Numbers

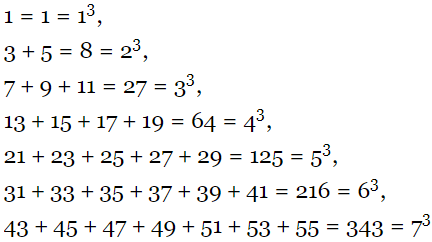
Number of consecutive odd number to add to get "n³" = n

2. Cubes and Their Prime Factors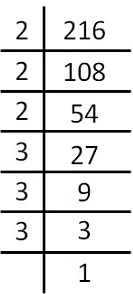

216 = 2 x 2 x 2 x 3 x 3 x3
Since each factor appears 3 times. 216 = (2³ × 3³) = 6³  because aⁿ x bⁿ = (a × b)ⁿ 

Example: Is 354 a perfect cube?

Sol: 354= 2×3×59
In the above factorization 2×3×59 remain.

Therefore, 354 is not a perfect cube.

Smallest Multiple that is a perfect cube

Example : Is 392 a perfect cube? If not, find the smallest natural number by which 392 must be multiplied so that the product is a perfect cube.

 Sol: 392 = 2 × 2 × 2 × 7 × 7 The prime factor 7 does not appear in a group of three. Therefore, 392 is not a perfect cube. To make its a cube, we need one more 7. In that case 392 × 7 = 2 × 2 × 2 × 7 × 7 × 7 = 2744  which is a perfect cube. Hence the smallest natural number by which 392 should be multiplied to make a perfect cube is 7.

Cube Roots

Lets understand an example -
There is a cube of volume 125 cm³ . Since all the side of cube is equal we want to find the length of our cube.
Volume of cube = (side of cube)³ unit³. ------------------------------------(1)
Side of cube =  (Volume of cube)^1/3.

Hence the side of any cube is nothing but a cube root of the volume of that cube.
How to denote cube root in mathematics.
Let's understand:  (25)^1/3 = (5³)^1/3 = 5. 

Hence let's take an integer x then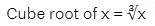

Cube Root Through Prime Factorization Method

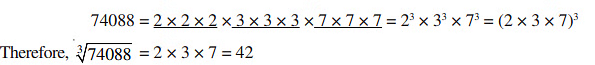
Example :  Find the cube root of 8000.

 Sol: Prime factorization of 8000 is 2 × 2 × 2 × 2 × 2 × 2 × 5 × 5 × 5 

So,   = 2 × 2 × 5 = 20

What we have discussed

• Numbers like 1729, 4104, 13832, are known as Hardy – Ramanujan Numbers. They can be expressed as sum of two cubes in two different ways. 
•  Numbers obtained when a number is multiplied by itself three times are known as cube numbers. For example 1, 8, 27, ... etc. 
• If in the prime factorization of any number each factor appears three times, then the number is a perfect cube. 
• The symbol 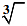   denotes cube root. For example  
  
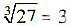  Question for Chapter Notes: Cubes & Cube Roots

  Try yourself:

  Which of the following numbers is a perfect cube?

  • A.

    1729
  • B.

    4104
  • C.

    13832
  • D.

    125

  Explanation

  - A perfect cube is a number that can be obtained by multiplying a number by itself three times.
  - In this case, only Option D, 125, satisfies this condition as 5 multiplied by itself three times results in 125.
  - Therefore, Option D is the correct answer.
  
  Note: It is important to note that while options A, B, and C are known as Hardy-Ramanujan Numbers, they are not perfect cubes as they cannot be expressed as the cube of a single integer.

  Report a problem

  Cancel Report

  View Solution