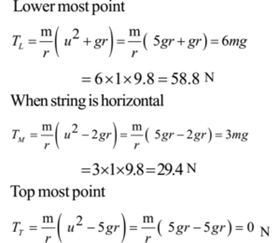Vertical Circular Motion - JEE PDF Download

We already know a bit about circular motion. It's a kind of movement where an object stays at the same distance from a fixed point. Circular motion is divided into two types: uniform and non-uniform. Examples include swinging a ball on a string or a car turning on a track. Now, let's talk about a special kind of circular motion called vertical circular motion.

Vertical Circular Motion

Imagine an object connected to a string and rotated around in a circle vertically.

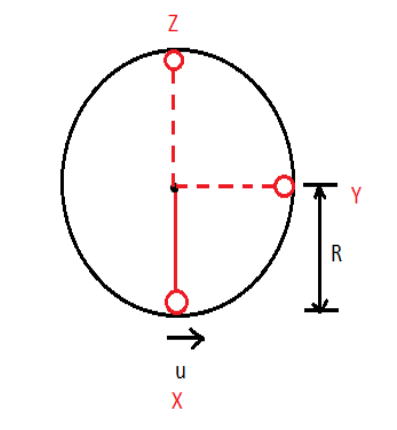Vertical Circular Motion

Between points X and Y, the tension in the string balances the weight, keeping it taut. To find the velocity needed to reach Y, we use conservation of mechanical energy. 

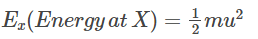
Since the particle just reaches Y, its velocity at Y is zero. 

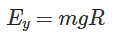
By equating the initial and final energy, we determine the velocity.

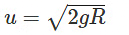
Now, if we want to find the minimum velocity to reach Z, assuming zero velocity at Z is incorrect. Velocity at Z should be such that weight equals centripetal force, making tension zero.

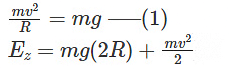
Substituting the velocity value, 

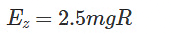
Now we equate energies for X and Z. 

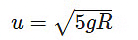
The critical values lead to three cases:

1. The ball oscillates and never reaches Y.

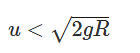
2. The ball loses contact between Y and Z, starting projectile motion.

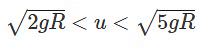
3. The string never becomes slack, completing the circle.

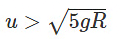
This situation is similar for a ball tied to a rod moving in a vertical circle. The only difference is that the velocity at the top can be zero, as the normal reaction of the rod balances the weight. 

Solving similarly yields three cases for a rod:

1. The body oscillates and doesn't reach Y.

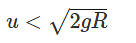
2. The ball oscillates, crosses Y, but doesn't reach Z.

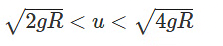
3. The body completes the circle.

Solved Examples on Vertical Circular Motion

Example 1: A stone is moving in a vertical circle up and down, using a string, like this.

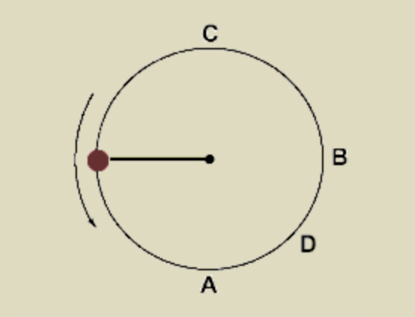
The string will have least tension at which point?

Solution: The right answer is C. The tension is highest at point A because it has to counteract the gravitational force (mg) and provide the extra force needed for the circular motion. At point C, tension is the lowest because some of the centripetal force is balanced by the gravitational force. This is shown in the diagram below.

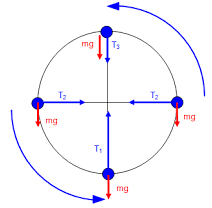
Example 2: A stone weighing 1 kg is whirled in a vertical circle at the end of a rope of length 0.5 m. Find the tension in the string at a) lowest position b) midway when the string is horizontal c) topmost position to just complete the circle. 

Solution: