Linear Search & Binary Search- 1 - GATE PDF Download
| Table of contents |

|
| Linear Search |

|
| Linear Search Algorithm |

|
| Pseudocode |

|
| Analysis |

|
| Code Implementation: |

|
| Binary Search |

|
| Binary Search Algorithm |

|
| Code Implementation |

|
Linear Search
Linear search is also called as sequential search algorithm. It is the simplest searching algorithm. In Linear search, we simply traverse the list completely and match each element of the list with the item whose location is to be found. If the match is found, then the location of the item is returned; otherwise, the algorithm returns NULL.
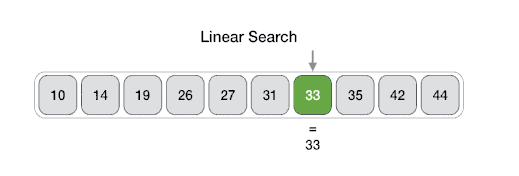
For example in above diagram, we are searching for an element 33. Therefore, the linear search method searches for it sequentially from the very first element until it finds a match. This returns a successful search.
Linear Search Algorithm
Step 1: Start from the 0th index of the input array, comparing the key value with the value at the 0th index.
Step 2: If the value matches the key, return the position at which the value was found.
Step 3: If the value does not match the key, compare the next element in the array.
Step 4: Repeat Step 3 until a match is found. Return the position at which the match was found.
Step 5: If it is an unsuccessful search, print that the element is not present in the array and exit the program.
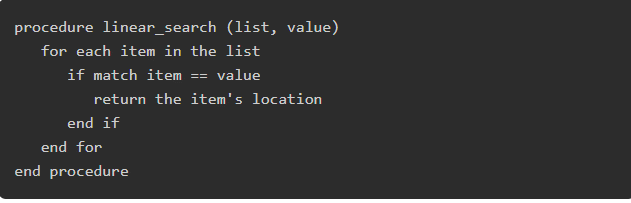
Pseudocode
Analysis
- Best Case: Linear search sequentially traverses through every element, making the best-case time complexity O(1) when the element is found in the first iteration.
- Worst Case: In the case of an unsuccessful search, where the key value is not found, linear search performs n iterations, resulting in a worst-case time complexity of O(n).
- Average Case: The average case time complexity of linear search is O(n).
Example: Let us look at the step-by-step searching of the key element (say 47) in an array using the linear search method.
Step 1: The linear search starts from the 0th index. Compare the key element with the value in the 0th index, 34.
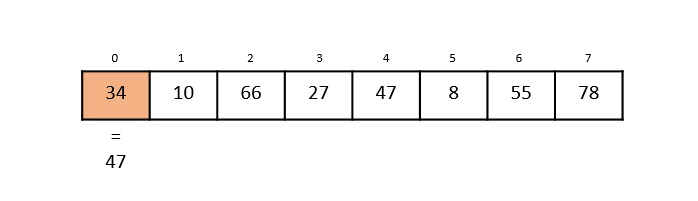 However, 47 ≠ 34. So it moves to the next element.
However, 47 ≠ 34. So it moves to the next element.
Step 2: Now, the key is compared with value in the 1st index of the array.
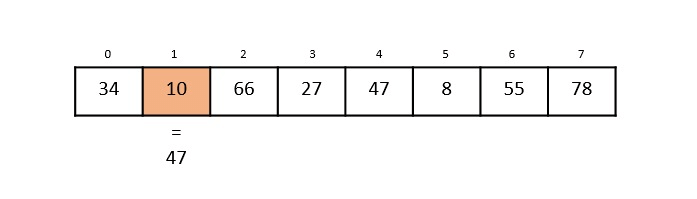
Still, 47 ≠ 10, making the algorithm move for another iteration.
Step 3: The next element 66 is compared with 47. They are both not a match so the algorithm compares the further elements.
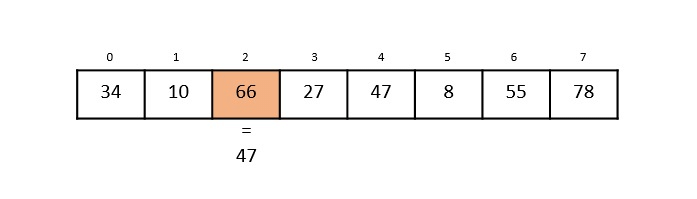
Step 4: Now the element in 3rd index, 27, is compared with the key value, 47. They are not equal so the algorithm is pushed forward to check the next element.
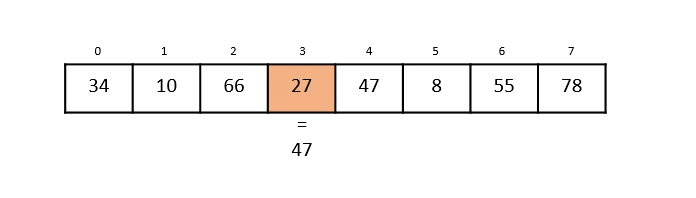
Step 5: Comparing the element in the 4th index of the array, 47, to the key 47. It is figured that both the elements match. Now, the position in which 47 is present, i.e., 4 is returned.
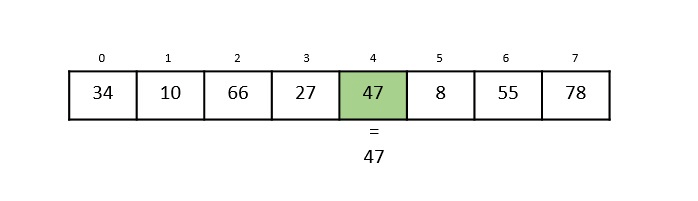
The output achieved is “Element found at 4th index”.
Code Implementation:
C
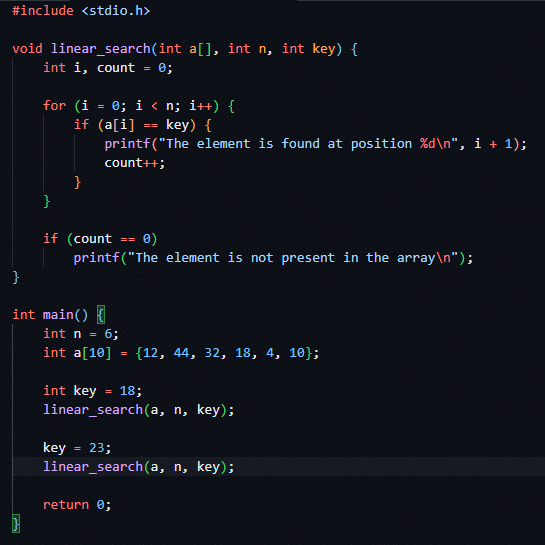

C++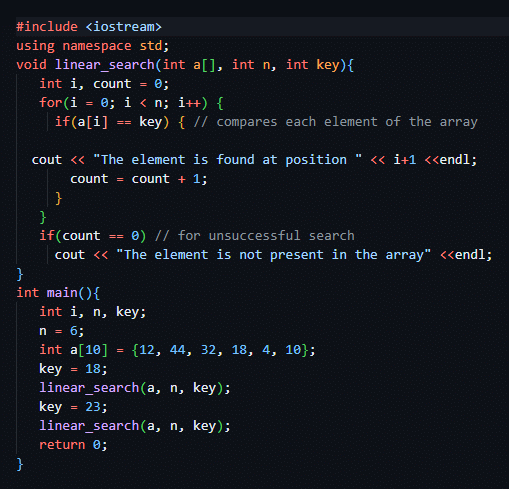
 Python
Python
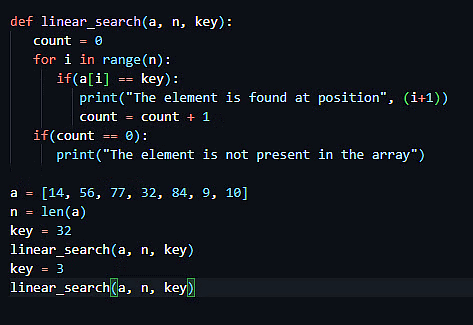

Java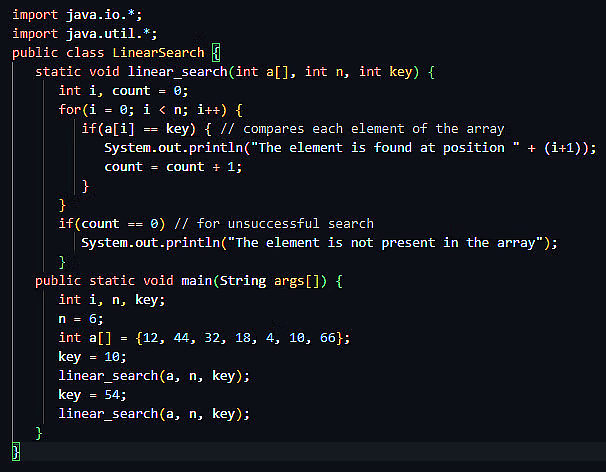
 Binary Search
Binary Search
Binary search is a fast search algorithm with run-time complexity of Ο(log n). This search algorithm works on the principle of divide and conquer, since it divides the array into half before searching. For this algorithm to work properly, the data collection should be in the sorted form.
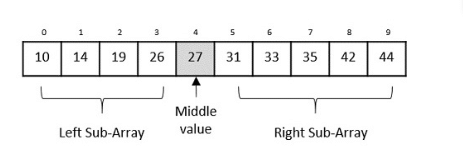
Binary search aims to find a specific key value by examining the middle item of a collection. If a match is found, it returns the index of that item. However, if the middle item's value is higher than the key value, it looks in the right sub-array. Otherwise, it checks the left sub-array. This process continues recursively until the size of the subarray becomes zero.
- Binary search locates a target value by checking the middle item in the collection.
- If there's a match, it gives back the index of the item.
- If the middle item's value is greater than the target value, it searches the right sub-array.
- If the middle item's value is less than the target value, it searches the left sub-array.
- This procedure repeats recursively until the subarray size becomes zero.
Binary Search Algorithm
Step 1: Select the middle item in the array and compare it with the target value. If they match, return the position of the middle item.
Step 2: If there's no match, determine whether the target value is greater than or less than the middle item's value.
Step 3: If the target value is greater, search in the right sub-array. If it's lower, search in the left sub-array.
Step 4: Repeat Steps 1, 2, and 3 iteratively until the size of the sub-array becomes 1.
Step 5: If the target value is not found in the array, the search is considered unsuccessful.
Pseudocode
Analysis
The time complexity of the binary search algorithm is O(log n).
For a binary search to work, it is mandatory for the target array to be sorted. We shall learn the process of binary search with a pictorial example. The following is our sorted array and let us assume that we need to search the location of value 31 using binary search.

First, we shall determine half of the array by using this formula −
mid = low + (high - low) / 2
Here it is, 0 + (9 - 0) / 2 = 4 (integer value of 4.5). So, 4 is the mid of the array.

Now we compare the value stored at location 4, with the value being searched, i.e. 31. We find that the value at location 4 is 27, which is not a match. As the value is greater than 27 and we have a sorted array, so we also know that the target value must be in the upper portion of the array.

We change our low to mid + 1 and find the new mid value again.
low = mid + 1 mid = low + (high - low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value 31.
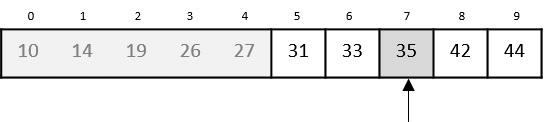
The value stored at location 7 is not a match, rather it is less than what we are looking for. So, the value must be in the lower part from this location.

Hence, we calculate the mid again. This time it is 5.
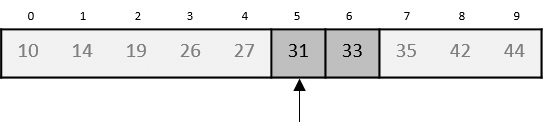
We compare the value stored at location 5 with our target value. We find that it is a match.

We conclude that the target value 31 is stored at location 5.
Binary search halves the searchable items and thus reduces the count of comparisons to be made to very less numbers.
Code Implementation
C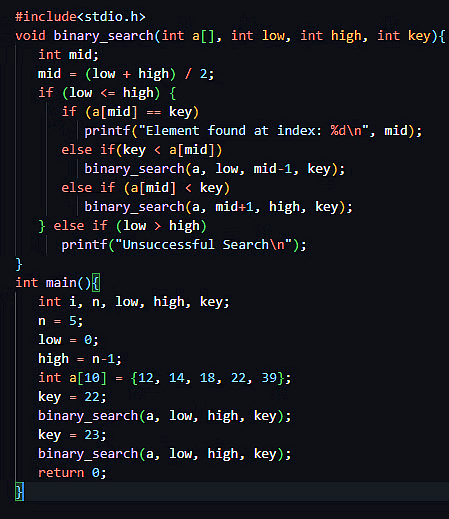

C++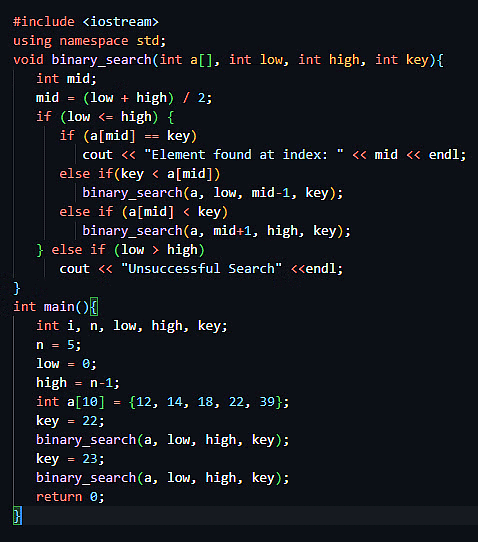

Python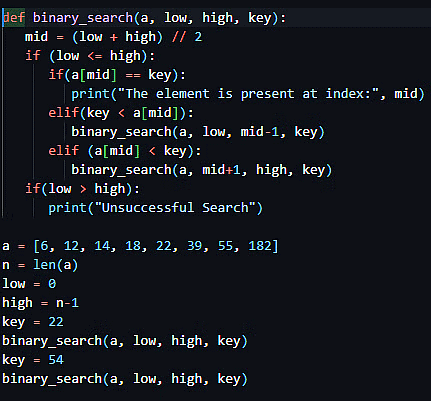

Java

FAQs on Linear Search & Binary Search- 1 - GATE
| 1. What is linear search? |  |
| 2. How does linear search work? |  |
| 3. What is the time complexity of linear search? |  |
| 4. When is linear search most suitable? |  |
| 5. What are the advantages and disadvantages of linear search? |  |


















