JEE Advanced Previous Year Questions (2018 - 2023): Laws of Motion | Physics for JEE Main & Advanced PDF Download
2023
Q1: A particle of mass m is moving in the xy-plane such that its velocity at a point (x,y) is given as
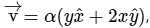 where α is a non-zero constant. What is the force
where α is a non-zero constant. What is the force 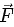 acting on the particle?
acting on the particle? (a)
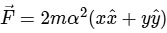
(b)
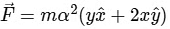
(c)
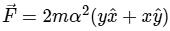
(d)
 [JEE Advanced 2023 Paper 2]
[JEE Advanced 2023 Paper 2]Ans: (a)
Given :
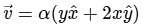
For the x-component,
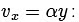
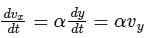
Given vy = 2αx:
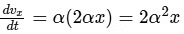
For the y-component, vy = 2αx:
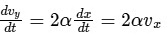
Given vx = αy
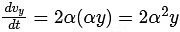
Thus, combining the components :
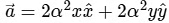
Now, the force acting on the particle is given by :
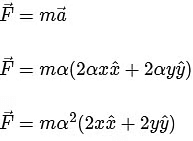
This is equivalent to :
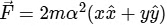
The correct answer is Option A :

2021
Q1: A projectile is thrown from a point O on the ground at an angle 45∘ from the vertical and with a speed 5√2 m/s. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, 0.5 s after the splitting. The other part, t seconds after splitting, falls to the ground at a distance x meters from the point O. The acceleration due to gravity g = 10 m/s2.
The value of t is _____________. [JEE Advanced 2021 Paper 1 ]
Ans: 0.5
 Range =
Range = 
Time of flight =

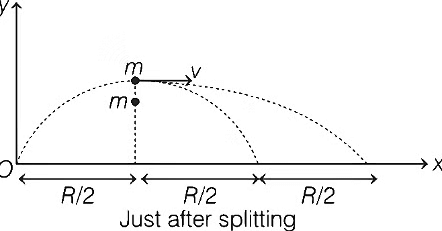
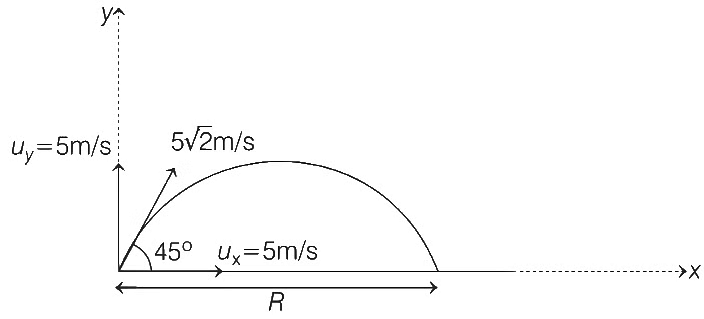
Both particle have no vertical velocity after splitting so both will take same time to reach the ground.
∵ Time of motion of one part falling vertically downwards is 0.5 s
⇒ Time of motion of another part, t = 0.5 s
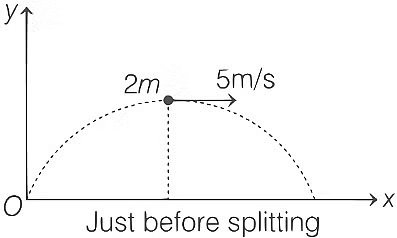
Q2: A projectile is thrown from a point O on the ground at an angle 45∘ from the vertical and with a speed 5√2 m/s. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, 0.5 s after the splitting. The other part, t seconds after splitting, falls to the ground at a distance x meters from the point O. The acceleration due to gravity g = 10 m/s2.
The value of x is _____________. [JEE Advanced 2021 Paper 1 ]
Ans: 7.5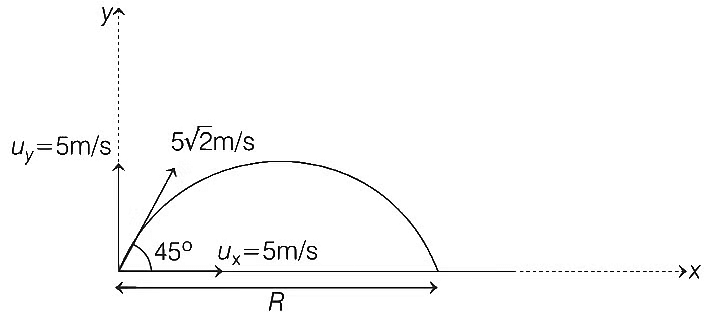
Range = 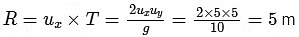
Time of flight = 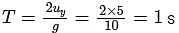
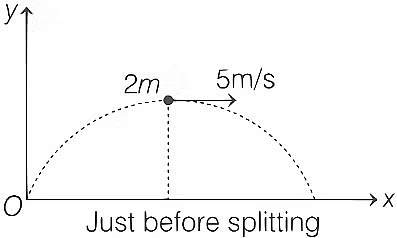

Both particle have no vertical velocity after splitting so both will take same time to reach the ground.
∵ Time of motion of one part falling vertically downwards is 0.5 s
⇒ Time of motion of another part, t = 0.5 s
From momentum conservation, pi = pf
2m × 5 = m × v
v = 10 m/s
Displacement of other part in 0.5 s in horizontal direction,
= v(T/2) = 10 × 0.5 = 5 m = R
∴ Total distance of second part from point O is x =3R/2 = 3 × 5/2
⇒ x = 7.5 m
2020
Q1: Put a uniform meter scale horizontally on your extended index fingers with the left one at 0.00 cm and the right one at 90.00 cm. When you attempt to move both the fingers slowly towards the center, initially only the left finger slips with respect to the scale and the right finger does not. After some distance, the left finger stops and the right one starts slipping. Then the right finger stops at a distance xR from the center (50.00 cm) of the scale and the left one starts slipping again. This happens because of the difference in the frictional forces on the two fingers. If the coefficients of static and dynamic friction between the fingers and the scale are 0.40 and 0.32, respectively, the value of xR (in cm) is ______. [JEE Advanced 2020 Paper 1]
Ans: 25.60
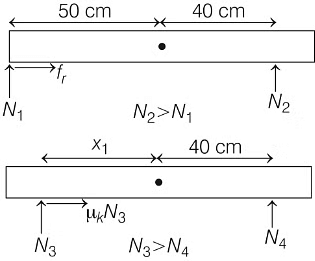
Here, μs = 0.40, μk = 0.32
∵ μkN3 = μsN4
and x1N3 = 40 × N4
So, 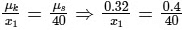
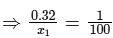
∴ x1 = 32 cm
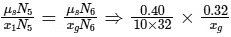
⇒ xg = 25.6
Q2: A football of radius R is kept on a hole of radius r (r < R) made on a plank kept horizontally. One end of the plank is now lifted so that it gets tilted making an angle θ from the horizontal as shown in the figure below. The maximum value of θ so that the football does not start rolling down the plank satisfies (figure is schematic and not drawn to scale) [JEE Advanced 2020 Paper 1]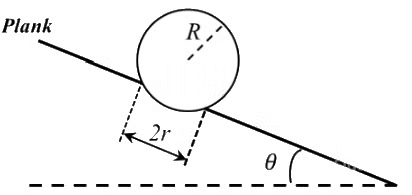
(a) sin θ = r / R
(b) tan θ = r / R
(c) sin θ = r / 2R
(d) cos θ = r / 2R
Ans: (a)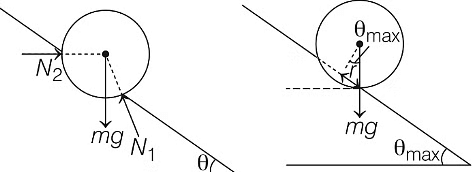
For θmax, the football is about to roll, then N2 = 0 and all the forces (mg and N1) must pass through contact point.
∴ 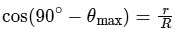
⇒ sin θmax = r / R
2019
Q1: A block of mass 2M is attached to a massless spring with spring-constant k.This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1, a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0. Which of the following option(s) is/are correct? [g is the acceleration due to gravity. Neglect friction]
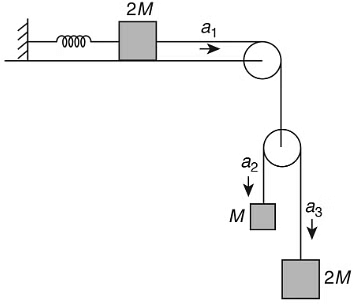 (a) a2 − a1= a1 − a3
(a) a2 − a1= a1 − a3(b) At an extension of x0 / 4 of the spring, the magnitude of acceleration of the block connected to the spring is 3g / 10.
(c) x0 = 4Mg / k
(d) When spring achieves an extension of x0 / 2 for the first time, the speed of the block connected to the spring is
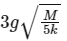 [JEE Advanced 2019 Paper 2]
[JEE Advanced 2019 Paper 2]Ans: (a)
 In the frame of pulley B,
In the frame of pulley B,
the hanging masses have accelerations :
M → (a2 − a1)
2M → (a3 − a1) : downward.
∴ (a2 − a1) = (−a3 − a1) [constant]
Assuming that the extension of the spring is x
We consider the FBD of A :
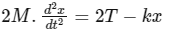

where, a1 = d2x / dt2 .... (i)
and the FBD of the rest of the system in the frame of pulley B :
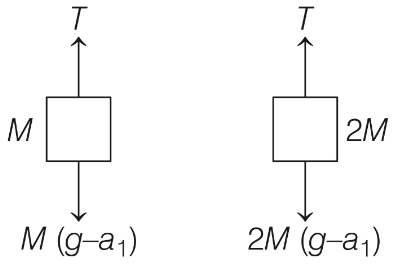
Upward acceleration of block M w.r.t. the pulley B = Downward acceleration of block 2M w.r.t. the pulley.
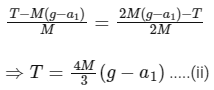
Substituting in Eq. (i), we get
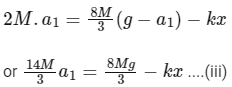
This is equation of SHM
Maximum extension = 2 × amplitude
i.e., 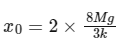
Amplitude = x0 / 2 = 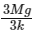 and ω =
and ω = 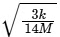
At x0 / 4, acceleration is easily found from Eq. (iii),
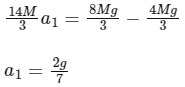
At x0/2, speed of the block
(2M) = ω x Amplitude
= 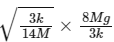
∴ option (a) is correct.
2018
Q1: A solid horizontal surface is covered with a thin layer of oil. A rectangular block of mass m = 0.4 kg is at rest on this surface. An impulse of 1.0N is applied to the block at time t = 0 so that it starts moving along the x-axis with a velocity v(t) = v0e−t/τ, where �0 is a constant and τ = 4s. The displacement of the block, in metres, at t = τ is ______________ Take e−1= 0.37. [JEE Advanced 2018 Paper 2]
Ans: 6.30
The block was initially at rest and its velocity just after the application of impulse is v(0) = v0e−0/τ = v0. The applied impulse is equal to the change in linear momentum of the block i.e., J = mv0, which give
v0 = J/m = 1/0.4 = 2.5 m/s.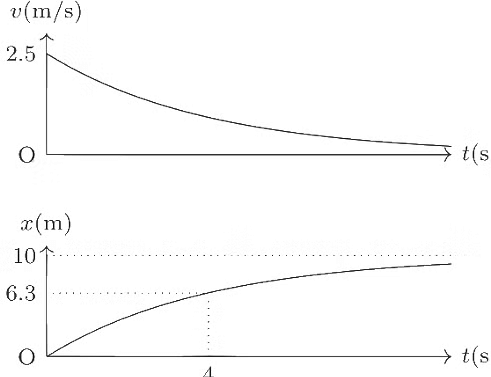
The velocity of the particle is given as
v(t) = v0e−t/τ
Integrate to get the displacement
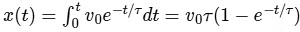 Substitute t = τ = 4 s and
Substitute t = τ = 4 s and
v0 = 2.5 m/s to get x(τ)
= (2.5) (4) (1 − e−1)
= 6.3 m.
|
289 videos|635 docs|179 tests
|

|
Explore Courses for JEE exam
|

|

















