CAPM (Capital Asset Pricing Model) - 2 | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Capital Asset Pricing Model (CAPM) |

|
| Assumptions underpinning the CAPM |

|
| Applications of the CAPM |

|
| Limitations of the CAPM |

|
| Conclusion |

|
Capital Asset Pricing Model (CAPM)
- In this segment, we will delve into the computation of estimated asset returns using the risk-free rate, the market rate of return, and the assigned asset betas. The CAPM formula typically incorporates the risk-free rate as:

- The above expression shows that the main factor in the determination of the expected return for security is its beta. The second part of the expression is positive which means that there exists a positive relationship between the beta of an asset and the expected return of the asset. In other words, the higher the beta of an asset, the higher will be its expected return. The model provides a linear relationship between the expected return–beta that determines the expected return of an asset, given its beta. The beta also explains how well the asset correlates with the market. If 𝛽𝑖 >1 i.e., assets with a beta greater than 1 will have a higher expected return than that of the market return, whereas if 𝛽𝑖 < 1 i.e., assets with a beta of less than 1 expected return of the asset will be less than the market return.
- Occasionally, assets with low beta prove beneficial to a portfolio by mitigating its overall risk, even if the asset's return falls below the risk-free rate. Such assets may possess a negative beta, indicating that their required return is lower than the risk-free rate. Take insurance, for instance, which yields a positive return for investors when the insured party experiences a sudden loss. However, the insurance premium must be paid regardless of whether such a loss occurs. Consequently, insurance exhibits a negative beta and an expected return below zero. Nonetheless, including insurance in a portfolio serves to diminish the portfolio's overall risk.
- The Capital Asset Pricing Model (CAPM) stands out as one of the simplest yet most potent tools in portfolio theory. Developed by William Sharpe, John Lintner, Jack Treynor, and Jan Mossin, the model builds upon Harry Markowitz's groundwork on diversification and modern portfolio theory. Assets sharing the same beta are expected to yield identical returns, regardless of their specific characteristics. Hence, according to the risk-return relationship, assets are solely defined by their beta risk.
Illustration 1:
Let's consider a scenario where the risk-free rate stands at 5 percent, the expected return on the market portfolio is 25 percent, with a standard deviation of 50 percent. Now, take a Chinese company, Alibaba, with a standard deviation of 85 percent but uncorrelated with the market. We need to calculate Alibaba's beta and expected return.

Illustration 2:
Suppose the risk-free rate is 6 percent, the expected return on the market portfolio is 25 percent, and its standard deviation is 33 percent. A Canadian company, Faces Canada, has a standard deviation of 45 percent and a correlation of 0.35 with the market. Calculate Faces Canada’s beta and expected return.
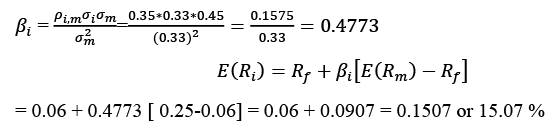
Assumptions underpinning the CAPM
- Risk-averse, utility-maximizing, rational investors: The CAPM operates under the assumption that investors are risk-averse, seeking to maximize their utility. Although risk aversion levels may vary among individuals, the model suggests that investors demand compensation for the risks they undertake. Systematic risk factors into this equation, offering higher returns to mitigate the additional risk assumed by risk-averse investors. Furthermore, investors are deemed rational, capable of accurately evaluating available information to make informed decisions. While rational investors may arrive at differing estimates of expected risk and returns, they remain rational in their decision-making process. This assumption aligns with economic theories that view consumers as utility maximizers and risk-averse, providing a realistic portrayal of market behavior.
- Frictionless markets: The CAPM operates within the framework of frictionless markets, where operational characteristics are abstract and devoid of obstacles. In these idealized markets, transaction costs and taxes are absent, ensuring that trading volumes or prices do not disrupt the risk-return relationship of securities. Additionally, frictionless markets do not impose costs or restrictions on short selling, assuming that borrowing and lending occur at the same rate as the risk-free rate.
- Investors plan for the same single holding period: The CAPM assumes that investors make decisions within a single period, rendering it a single-period model. Although a multi-period model offers more comprehensive insights, it presents challenges and complexities. Despite the limitations of a single holding period, the CAPM's application to a multi-period horizon remains viable, albeit with potential trade-offs and sub-optimal decisions in achieving maximizing outcomes across multiple periods.
- Homogeneous expectations or beliefs among investors: The CAPM operates under the assumption that all investors share the same probability distributions and utilize identical inputs for assessing future cash flows. Additionally, investors are presumed to be rational, arriving at uniform valuations. Consequently, with similar asset valuations, investors will opt for or generate the same optimal risky portfolio, known as the market portfolio.
- Infinitely divisible investments: Under this assumption, individuals have the flexibility to invest any desired amount in an asset, regardless of size. This facilitates the use of continuous functions in the model, avoiding the need for discrete jump functions. While this assumption does not directly impact the model's implications, it enhances the model's accessibility and understanding for investors.
- Investors as price takers: In the CAPM framework, investors are regarded as price takers, implying that no single investor possesses sufficient influence to impact market prices. The model assumes a large number of investors whose trades do not significantly affect security prices. Although prices of small stocks may be susceptible to investor activity, their impact on the primary estimates of the CAPM is considered negligible. Therefore, investors are deemed as price takers within this context.
The security MarketLine & CAPM
- The Capital Asset Pricing Model (CAPM) finds applications in pricing various securities across different scenarios, particularly through the Security Market Line (SML). The SML serves as a graphical depiction of the CAPM, with beta represented on the x-axis and the expected return of the security on the y-axis. Similar to the Capital Market Line (CML), the SML intersects the y-axis at the risk-free rate of return, while its slope is determined by the market risk premium (Rm – Rf).
- Unlike the CML, which pertains to portfolios on the efficient frontier, the SML is applicable to individual securities. While the efficient frontier reflects optimal combinations of expected return and total risk for investors, the SML caters to all securities, regardless of their efficiency. For efficient portfolios, where total risk equals systematic risk due to full risk diversification, the SML remains relevant.
- Figure 3 illustrates a graphical representation of the Security Market Line within the CAPM framework. On the x-axis, the market's beta is depicted as 1.0, while the expected rate of return (Rm) earned by the market is indicated on the y-axis. Points along this line aid in estimating the expected return of an asset solely based on its systematic risk. At point M, the systematic risk of both the market and the security align, indicating that the expected returns from the security mirror those of the market. The positive and linear relationship between beta and expected return suggests that an increase in beta results in a higher expected return from the security, given the risk-free rate prevailing in the market.

The Security Market Line
Applications of the CAPM
- The predictive power of the CAPM regarding risk and the relationship between risk and return makes it very powerful and appealing. There is a large number of practical applications of the CAPM that may not be true from a theoretical perspective. In this section, we will discuss the common applications of the model. We will see that the CAPM and the SML took together will indicate the direction of the market returns at the given level of risk under different situations.
- However, the results may indicate that the actual return may be quite different from the expected return which helps to evaluate whether a security is overvalued, undervalued or fairly valued. Other major applications of the CAPM include computation of the estimates of the expected return for capital budgeting, the performance appraisal of the portfolio manager can also be done by comparing the actual return of a portfolio and the CAPM return estimated by the portfolio manager, and the output from the model also helps in the selection of the security based on the analysis of alternate return estimates and the CAPM returns.
- For example, we've employed CAPM to calculate the anticipated return of an asset based on its systematic risk. This estimate serves as a crucial benchmark for evaluating investments in various assets such as stocks, bonds, real estate, and other financial instruments. Similarly, in the realm of capital budgeting, determining the economic viability of projects relies heavily on the estimated required rate of return derived from CAPM. This rate guides decision-makers in selecting the most suitable projects for the company's capital allocation.
- Analytical tools like the net present value of a project and its associated investments and cash flows are also contingent on estimates of cash flows discounted at the required rate of return, which is often determined using CAPM. Consequently, CAPM finds widespread application in estimating expected returns across numerous scenarios, including computing the cost of capital for companies under regulatory oversight and establishing fair insurance premiums.
Limitations of the CAPM
Despite its utility, the CAPM is encumbered by both theoretical and practical limitations. Theoretical limitations pertain to inherent constraints within the model's framework, while practical limitations arise during its application.
Theoretical Limitations:
- In the CAPM's single-factor model, only systematic risk, or beta risk, is factored into asset pricing, neglecting other investment characteristics. This restricts the model's flexibility and comprehensiveness.
- Furthermore, the CAPM's prescriptive nature, though advantageous for its simplicity, fails to offer multi-period predictions or insights into future investment objectives, potentially leading to myopic decision-making.
Practical Limitations:
In practice, implementing the CAPM presents significant challenges:
- True Market Portfolio: The CAPM posits the existence of a "true" market portfolio comprising all investible and non-investible assets across various asset classes, including human capital and assets in closed economies. However, verifying CAPM estimates for assets within this comprehensive portfolio is challenging due to the unobservability of certain components.
- Market Portfolio Proxies: In the absence of accurate data, analysts resort to creating proxies for the market portfolio. These proxies vary based on different assumptions, geographic regions, and other factors, resulting in disparate return estimates for the same asset. Such variability conflicts with the CAPM's framework.
- Estimating systematic risk: Adequate historical data is essential for estimating beta risk within the framework of the CAPM. However, there are instances where the historical performance of a company may not accurately reflect its current or future state. Despite the CAPM being an ex-ante model, the beta estimates derived from it rely on ex-post data. Consequently, variations in the time periods used for estimation can lead to disparate beta estimates.
- Limited predictive power: Empirical evidence suggests a weak correlation between CAPM estimates and realized returns, challenging the model's reliability in predicting asset returns. This discrepancy indicates that asset returns may not be solely determined by systematic risk, undermining the CAPM's effectiveness as a predictive tool. Given that investors base their investment decisions on anticipated future returns, the CAPM's poor predictive ability is a notable limitation.
- Uniformity in investor expectations: The CAPM assumes uniform investor expectations, resulting in a singular security market line and a single optimal risky portfolio for all investors. Relaxing this assumption would yield multiple optimal risky portfolios and diverse security market lines, reflecting the varying preferences and risk tolerances of investors. Consequently, investors would choose between different optimal portfolios based on their individual assessments, rather than relying on a single standardized framework.
[Question: 991119]"}" style="font-size:10pt;font-family:Arial;font-style:normal;">[Question: 991118]
Conclusion
In this module, we delved into the intricacies of the Capital Asset Pricing Model (CAPM), exploring its core concepts, underlying assumptions, and notable limitations. We emphasized its pivotal role in estimating asset returns based on systematic beta, shedding light on related topics such as the Capital Market Line (CML) and Security Market Line (SML). Understanding passive asset management strategies proved crucial, considering their relevance in varying market conditions. Investors strategically leveraged lending and borrowing at distinct rates to optimize their market portfolios for higher expected returns. Additionally, we scrutinized the distinction between systematic and non-systematic risk, discerning which risks are avoidable and which are inherent. Introducing beta, we elucidated its significance in gauging asset sensitivity to market fluctuations, elucidating the model's equation linking beta and expected return.
FAQs on CAPM (Capital Asset Pricing Model) - 2 - Management Optional Notes for UPSC
| 1. What are the key assumptions underlying the Capital Asset Pricing Model (CAPM)? |  |
| 2. How is the Capital Asset Pricing Model (CAPM) applied in financial analysis? |  |
| 3. What are the limitations of the Capital Asset Pricing Model (CAPM)? |  |
| 4. How can investors benefit from using the Capital Asset Pricing Model (CAPM) in their investment decisions? |  |
| 5. How does the Capital Asset Pricing Model (CAPM) help in estimating the cost of equity for a company? |  |

















