JEE Advanced Previous Year Questions (2018 - 2024): Rotational Motion | Physics for JEE Main & Advanced PDF Download
2024
Q1: A disc of mass M and radius R is free to rotate about its vertical axis as shown in the figure. A battery operated motor of negligible mass is fixed to this disc at a point on its circumference. Another disc of the same mass M and radius R/2 is fixed to the motor's thin shaft. Initially, both the discs are at rest. The motor is switched on so that the smaller disc rotates at a uniform angular speed ω. If the angular speed at which the large disc rotates is ω/n, then the value of n is ________. [JEE Advanced 2024 Paper 1]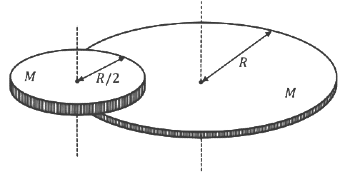 Ans: 12
Ans: 12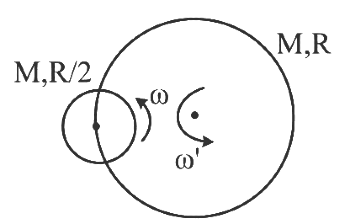 On applying conservation of angular momentum about axis of larger disc.
On applying conservation of angular momentum about axis of larger disc.
12 ⋅ M (R2) 2 ⋅ ω - M (ω' R) ⋅ R - MR²2 ⋅ ω' = 0
⇒ ω8 = 3ω'2
⇒ ω' = ω12
Hence, n = 12
Q2: A thin uniform rod of length L and certain mass is kept on a frictionless horizontal table with a massless string of length L fixed to one end (top view is shown in the figure). The other end of the string is pivoted to a point O. If a horizontal impulse P is imparted to the rod at a distance x = L/n from the mid-point of the rod (see figure), then the rod and string revolve together around the point O, with the rod remaining aligned with the string. In such a case, the value of n is ________. [JEE Advanced 2024 Paper 1]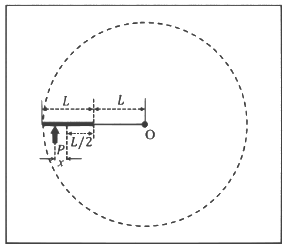 Ans: 18
Ans: 18
∫F dt = Δ momentum
= m (Vcm - 0)
P = m (ω rcm)
= mω (L + L2)
P = mω (3L2) ... (i)
∫τ dt = Δ angular momentum
∫ r × F dt = ΔL
r × ∫ F dt = I (ω - 0), and I is the moment of inertia about the axis of rotation.
(L + L2 + x) × P = (Icm + m d²) ω
= 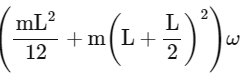
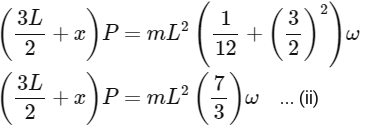
Divide eq.-(i) & (ii)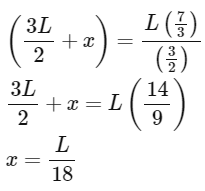
2023
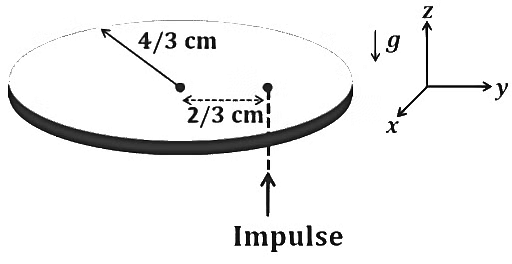
Q1: A thin circular coin of mass 5gm and radius 4/3 cm is initially in a horizontal xy-plane. The coin is tossed vertically up ( +z direction) by applying an impulse of √π/2 × 10−2 N-s at a distance 2/3 cm from its center. The coin spins about its diameter and moves along the +z direction. By the time the coin reaches back to its initial position, it completes n rotations. The value of n is ________.
[Given: The acceleration due to gravity g = 10 m s−2 ] [JEE Advanced 2023 Paper 2]
Ans: 30
A coin with a radius of mr = 4/3 × 10−2m and a mass of m = 5 × 10−3kg is thrown upwards. An impulse of linN s Jlin = √π/2 × 10−2N s is applied perpendicularly to the plane of the coin. This impulse is delivered at a distance of d = r/2 from the center of the coin.
Initially at rest, the coin experiences a change in linear momentum due to the applied linear impulse, leading to the equation :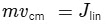
where m is the mass of the coin, vcm is its center of mass velocity after the impulse, and Jlin is the magnitude of the linear impulse.
After the impulse, the center of mass of the coin ascends with an initial velocity vcm. Under the influence of gravity, the coin returns to its original position in a time duration expressed by :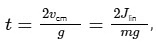
where g is the acceleration due to gravity, Jlin is the linear impulse applied, and m is the mass of the coin.
The coin undergoes rotation about its axis, and the angular impulse exerted on it around its center is described by the equation :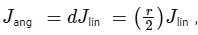
where Jang is the angular impulse, d is the distance from the center at which the linear impulse Jlin is applied, and r is the radius of the coin.
The angular impulse leads to a change in the angular momentum of the coin about a horizontal axis passing through its center. This relationship is given by :
where Icm is the moment of inertia of the coin about its center of mass, ω is the angular velocity after the impulse, and Lang is the angular momentum resulting from the angular impulse Jang.
The angular speed of the coin, denoted as ω, is determined by the equation :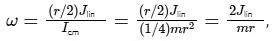
where r is the radius of the coin, Jlin is the linear impulse applied, m is the mass of the coin, and Icm is its moment of inertia about the center of mass.
After tossing, the angular speed of the coin remains constant because there is no external torque. The number of rotations \( n \) completed by the coin during the time \( t \) is calculated as :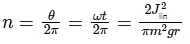
Substituting the given values, it becomes :
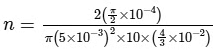
= 30
where θ is the total angular displacement, ω is the angular speed of the coin, Jlin is the linear impulse, m is the mass of the coin, g is the acceleration due to gravity, and r is the radius of the coin.
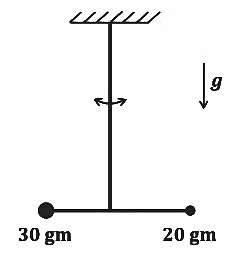
Q2: Two point-like objects of masses 20 gm and 30 gm are fixed at the two ends of a rigid massless rod of length 10 cm. This system is suspended vertically from a rigid ceiling using a thin wire attached to its center of mass, as shown in the figure. The resulting torsional pendulum undergoes small oscillations. The torsional constant of the wire is 1.2×10−8 N m rad−1. The angular frequency of the oscillations in n × 10−3 rad s−1. The value of n is _________ .
[JEE Advanced 2023 Paper 1]
 Ans: 10
Ans: 10
m1 = 30gm
m2 = 20 gm
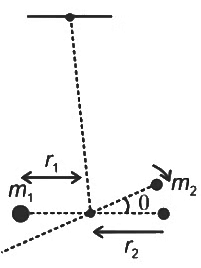
Moment of inertia about the axis of rotation is
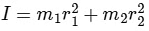
Clearly r1 = 4 cm
r2 = 6 cm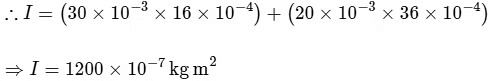
If the system is rotated by small angle ' θ ', the restoring torque is 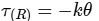
And 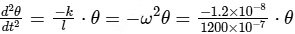
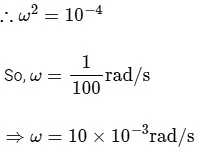
Q3: A bar of mass M = 1.00 kg and length L = 0.20 m is lying on a horizontal frictionless surface. One end of the bar is pivoted at a point about which it is free to rotate. A small mass m = 0.10 kg is moving on the same horizontal surface with 5.00 m s−1 speed on a path perpendicular to the bar. It hits the bar at a distance L/2 from the pivoted end and returns back on the same path with speed v. After this elastic collision, the bar rotates with an angular velocity ω.
Which of the following statement is correct?
(a) ω = 6.98 rad s−1 and v = 4.30 m s−1
(b) ω = 3.75 rad s−1 and v = 4.30 m s−1
(c) ω = 3.75 rad s−1 and v = 10.0 m s−1
(d) ω = 6.80 rad s−1 and v = 4.10 m s−1 [JEE Advanced 2023 Paper 1]
Ans: (a)
A bar, having a mass of M = 1 kg and a length of L = 0.2 m, is hinged at a point P. A particle with a mass of m = 0.1 kg moves in a direction perpendicular to the bar at a velocity of u = 5 m/s. This particle collides elastically with the bar at a point that is L/2 (0.1 m) away from the pivot point P. As a result of this collision, the bar begins to rotate with an angular velocity ω, and the particle recoils with a new velocity v. 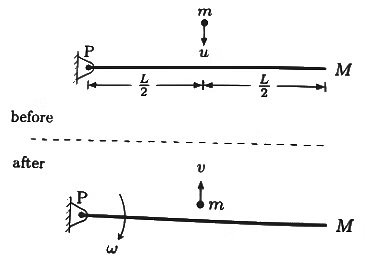
We can analyze the bar and the particle as a combined system. Initially, before the impact occurs, the system's angular momentum around the pivot point P is in a clockwise direction. The magnitude of this initial angular momentum can be expressed as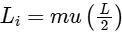
Following the collision, the angular momentum of the system about the pivot point P changes. This final angular momentum can be represented as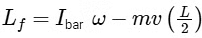
Here, Ibar, the moment of inertia of the bar, is given by 1/3ML2, and the term −1/2mvL accounts for the particle's contribution post-collision.
During the collision, the angular momentum of the system around the pivot point P is conserved. This means Li = Lf. Applying this principle, we derive the following relationship :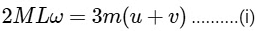
This equation represents the conservation of angular momentum in the system, correlating the initial and final states of the bar and the particle.
The kinetic energy of the system is conserved in an elastic collision. The kinetic energy of the system before the collision is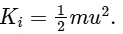
In an elastic collision, the total kinetic energy of the system is preserved. Prior to the collision, the kinetic energy of the system can be quantified as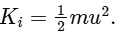
This equation denotes the initial kinetic energy, primarily attributed to the particle's motion.
After the collision takes place, the kinetic energy of the system can be expressed as :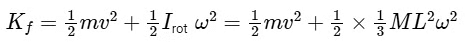
Here, the first term represents the kinetic energy due to the particle's velocity post-collision, and the second term represents the rotational kinetic energy of the bar.
By applying the principle of conservation of kinetic energy, which states Ki = Kf, we obtain the following relation :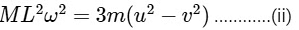
This equation links the initial and final kinetic energies of the system, comprising the particle and the rotating bar.
By resolving equations (i) and (ii), we determine that the velocity ω of the particle post-collision is 4.3 m/s and the angular velocity ω of the bar is 6.98 rad/s.
Q4: An annular disk of mass M, inner radius a and outer radius b is placed on a horizontal surface with coefficient of frictionμ, as shown in the figure. At some time, an impulse 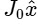 is applied at a height ℎ above the center of the disk. If ℎ = ℎm then the disk rolls without slipping along the x-axis. Which of the following statement(s) is(are) correct?
is applied at a height ℎ above the center of the disk. If ℎ = ℎm then the disk rolls without slipping along the x-axis. Which of the following statement(s) is(are) correct?
(b) For μ ≠ 0 and a → b, ℎm = b.
(c) For ℎ = ℎm, the initial angular velocity does not depend on the inner radius a.
(d) For μ = 0 and ℎ=0, the wheel always slides without rolling. [JEE Advanced 2023 Paper 2]
Ans: (a), (b), (c) & (d)
The moment of inertia Icm of an annular disc, with an inner radius a, an outer radius b, and a mass m, about an axis perpendicular to the disc and passing through its center C, is given by :
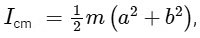
where a2 and b2 are the squares of the inner and outer radii, respectively.
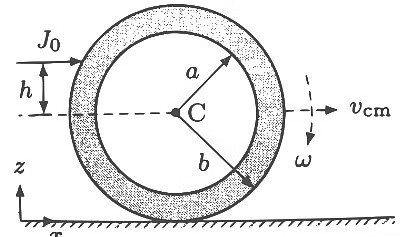
The linear impulse J0 alters the linear momentum of the disc. Right after the impulse is applied, the linear momentum can be represented as :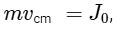
where m is the mass of the disc and vcm is the velocity of the center of mass resulting from the impulse.
The angular impulse about the center of mass C of the disc is applied in a clockwise direction, with its magnitude being J0,ang= ℎJ0. This impulse changes the angular momentum of the disc about point C, expressed as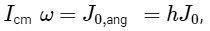
where Icm is the moment of inertia of the disc about its center of mass, ω is the angular velocity resulting from the angular impulse, J0 is the linear impulse, and ℎ is a factor relating the angular impulse to the linear impulse
For the disc to roll without slipping, given that the friction coefficient μ is non-zero, the condition is vcm = ωb. By substituting the expressions for vcm and ω and solving, we obtain the following relationship for the minimum value of ℎ (denoted as ℎm) :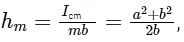
where Icm is the moment of inertia of the disc about its center of mass, m is the mass of the disc, a is the inner radius, and b is the outer radius of the disc.
By substituting a = 0 into the formula, we find that ℎm = b/2. This implies that a solid disc will roll without slipping if the impulse is applied midway along the upper half of the disc.
Similarly, substituting a = b yields ℎm = b. This indicates that a ring (an annular disc with equal inner and outer radii) will roll without slipping when the horizontal impulse is applied at the very top of the ring.
For the condition where ℎ = ℎm, the initial angular velocity ω is given by :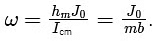
This expression for the angular velocity is independent of the inner radius a of the disc.
When a wheel is placed on a smooth surface with no friction (μ = 0) and an impulse is applied directly at its center (ℎ = 0), there is no torque generated to initiate rotation. Consequently, under these conditions, if an impulse is delivered to the center of a wheel on a frictionless surface, the wheel will invariably slide and not roll.
2022
Q1: At time t = 0, a disk of radius 1 m starts to roll without slipping on a horizontal plane with an angular acceleration of α = 2/3rads−2. A small stone is stuck to the disk. At t = 0, it is at the contact point of the disk and the plane. Later, at time t = √πs, the stone detaches itself and flies off tangentially from the disk. The maximum height (in m ) reached by the stone measured from the plane is 1/2 + x/10. The value of x is ____________ , [Take g =10 m s−2.] [JEE Advanced 2022 Paper 1 ]
Ans: 0.48 to 0.56
The angle rotated by disc in t = √πs is
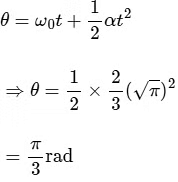
and the angular velocity of disc is
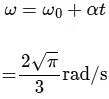
and 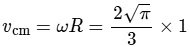
= 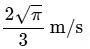
So, at the moment it detaches the situation is
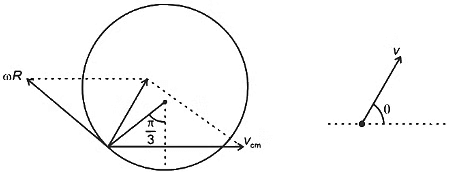
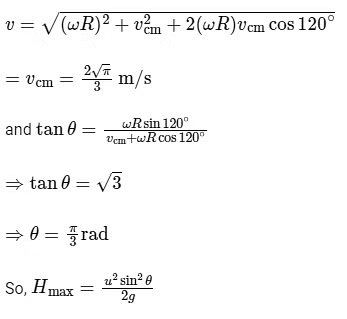
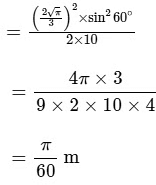
So, height from ground will be
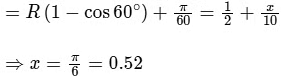
Q2: A flat surface of a thin uniform disk A of radius R is glued to a horizontal table. Another thin uniform disk B of mass M and with the same radius R rolls without slipping on the circumference of A, as shown in the figure. A flat surface of B also lies on the plane of the table. The center of mass of B has fixed angular speed ω about the vertical axis passing through the center of A. The angular momentum of B is nMωR2 with respect to the center of A.
Which of the following is the value of n ? [JEE Advanced 2022 Paper 2]
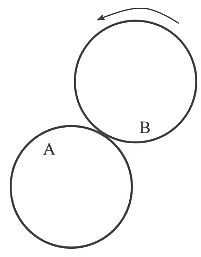 (a) 2
(a) 2
(b) 5
(c) 7/2
(d) 9/2
Ans: (b)
Angular momentum of B with respect to center of A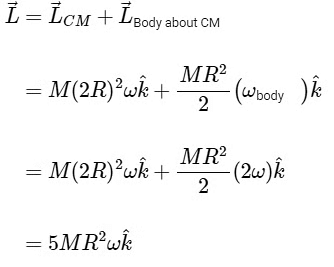
Comparing the magnitude with nMωR2
n = 2
Q2: A solid sphere of mass 1 kg and radius 1 m rolls without slipping on a fixed inclined plane with an angle of inclination θ = 30∘ from the horizontal. Two forces of magnitude 1 N each, parallel to the incline, act on the sphere, both at distance r = 0.5 m from the center of the sphere, as shown in the figure. The acceleration of the sphere down the plane is _________ ms−2.( Take g = 10ms−2)
[JEE Advanced 2022 Paper 1]
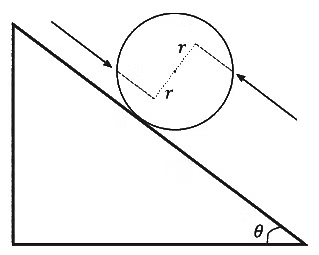
Ans: 2.80 to 2.92
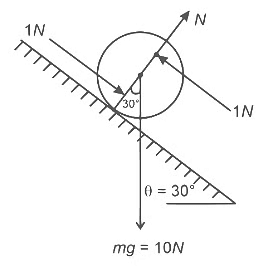
Taking torque about contact point.
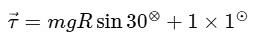
taking ⊗ is positive
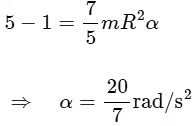
So, 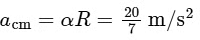
acm = 2.86 m/s2
2021
Q1: A thin rod of mass M and length a is free to rotate in horizontal plane about a fixed vertical axis passing through point O. A thin circular disc of mass M and of radius a/4 is pivoted on this rod with its center at a distance a/4 from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity Ω and the disc rotating about its vertical axis with angular velocity 4Ω. The total angular momentum of the system about the point O is
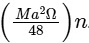 The value of n is ___________.
The value of n is ___________. [JEE Advanced 2021 Paper 1 ]
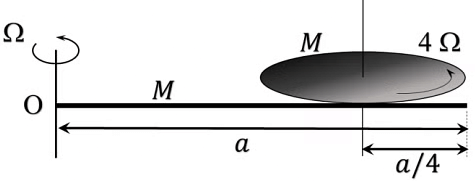
Ans: 49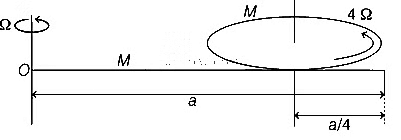
Angular momentum of disc about O is
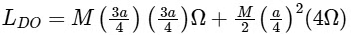
Angular momentum of rod about O is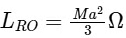
So, 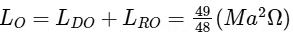
So, n = 49
Q2: A horizontal force F is applied at the center of mass of a cylindrical object of mass m and radius R, perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is μ. The center of mass of the object has an acceleration a. The acceleration due to gravity is g. Given that the object rolls without slipping, which of the following statement(s) is(are) correct? 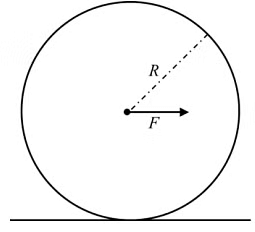 (a) For the same F, the value of a does not depend on whether the cylinder is solid or hollow(b) For a solid cylinder, the maximum possible value of a is 2μg
(a) For the same F, the value of a does not depend on whether the cylinder is solid or hollow(b) For a solid cylinder, the maximum possible value of a is 2μg
(c) The magnitude of the frictional force on the object due to the ground is always μmg
(d) For a thin-walled hollow cylinder, a = F/2m [JEE Advanced 2021 Paper 1]
Ans: (b) & (d)
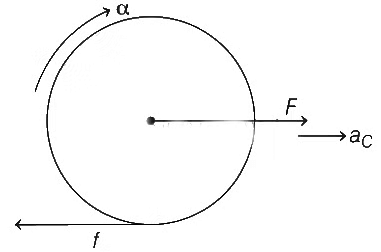
F − f = mac
fR = ICα
aC − αR = 0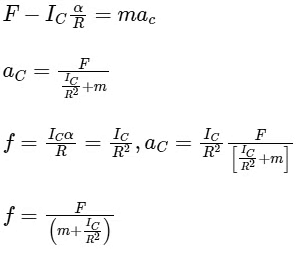
Thin walled hollow cylinder,
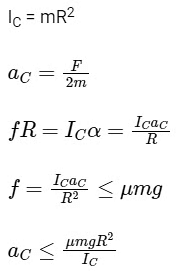
For solid cylinder, 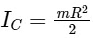
2020
Q1: A small roller of diameter 20 cm has an axle of diameter 10 cm (see figure below on the left). It is on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has moved 50 cm, the position of the scale will look like (figures are schematic and not drawn to scale) [JEE Advanced 2020 Paper 1]
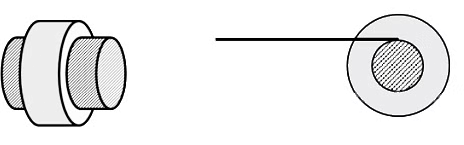
(a) 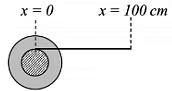
(b) 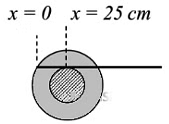
(c) 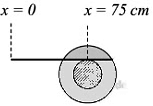
(d) 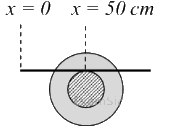
Ans: (c)
For no slipping at ground,
vc = ωR
(where, r is the radius of roller)
∴ Velocity of scale = (vc + ωr) (where, r is the radius of axle)
Given, vc . t = 50 cm
∴ Distance moved by scale = 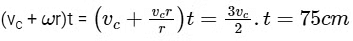
Therefore, relative displacement (with respect to centre of roller) is (75 − 50) cm = 25 cm.
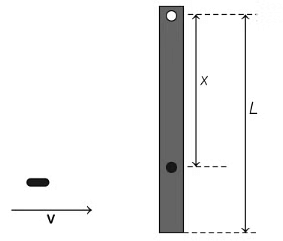
Q2: A rod of mass m and length L, pivoted at one of its ends, is hanging vertically. A bullet of the same mass moving at speed v strikes the rod horizontally at a distance x from its pivoted end and gets embedded in it. The combined system now rotates with angular speed ω about the pivot. The maximum angular speed ωM is achieved for x = xM. Then
(a) 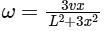
(b) 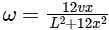
(c) 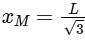
(d) 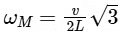 [JEE Advanced 2020 Paper 2]
[JEE Advanced 2020 Paper 2]
Ans: (a), (b) & (d)
According to conservation of angular momentum about suspension point,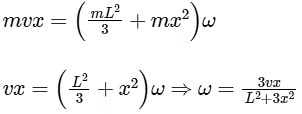
For maximum,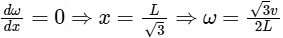
2019
Q1: A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is/are correct, when the rod makes an angle 60∘ with vertical? [g is the acceleration due to gravity]
(a) The angular acceleration of the rod will be 2g / L
(b) The normal reaction force from the floor on the rod will be Mg / 16
(c) The radial acceleration of the rod's center of mass will be 3g / 4
(d) The angular speed of the rod will be 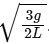 . [JEE Advanced 2019 Paper 2]
. [JEE Advanced 2019 Paper 2]
Ans: (b), (c) & (d)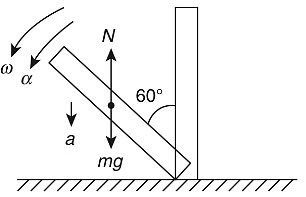
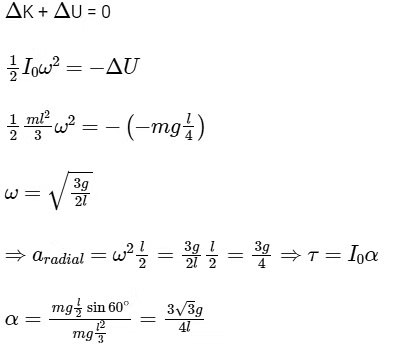
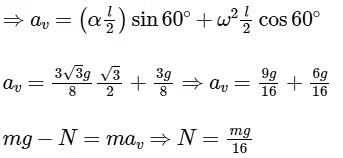
2018
Q1: Two vectors
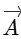 and
and 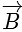 are defined as
are defined as 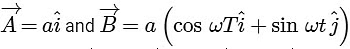 , where a is a constant and
, where a is a constant and 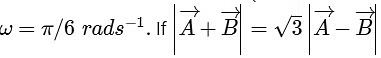 at time t = τ for the first time, the value of τ in second, is ______________. [JEE Advanced 2018 Paper 1]
at time t = τ for the first time, the value of τ in second, is ______________. [JEE Advanced 2018 Paper 1]Ans: 2
The vector 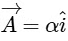 has a magnitude a and its direction is fixed. The vector
has a magnitude a and its direction is fixed. The vector 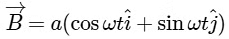 rotates with an angular speed ω =π / 6 rad/s in a circle of radius a. The magnitude of the sum and the difference of these vectors are given by
rotates with an angular speed ω =π / 6 rad/s in a circle of radius a. The magnitude of the sum and the difference of these vectors are given by
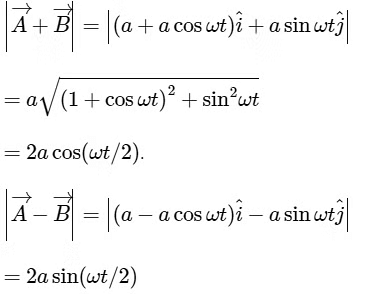
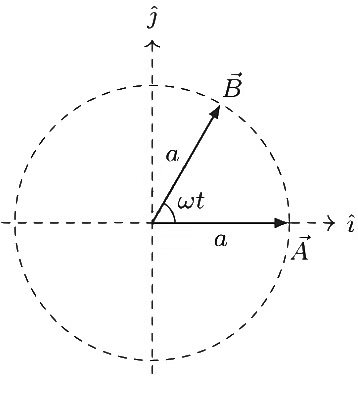
Hence,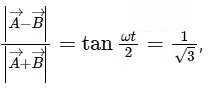
which gives t = τ = (2/ω)(π/6)
= 2 s.
Q2: The potential energy of a particle of mass m at a distance r from a fixed point O is given by 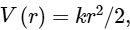 , where k is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius r about the point O. If v is the speed of the particle and L is the magnitude of its angular momentum about O, which of the following statements is (are) true?
, where k is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius r about the point O. If v is the speed of the particle and L is the magnitude of its angular momentum about O, which of the following statements is (are) true?
(a) 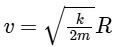
(b) 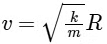
(c) 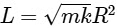
(d) 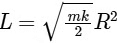
Ans: (b) & (c)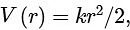
where k is positive constant, r is radius of circular orbit, V(r) is potential, v is speed of particle, L is angular momentum.
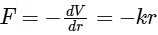 (towards centre)
(towards centre)
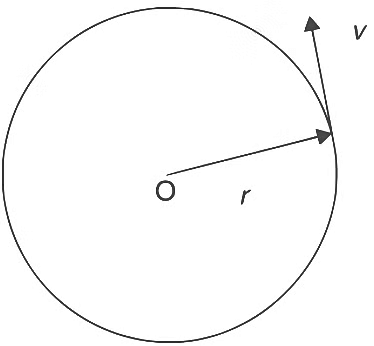
Kr = mv2 / R (Centripetal force)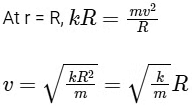
Hence, option (B) is correct.Also, we know L = mvR
Substitute the value of v, we get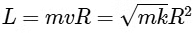
Hence, option (C) is correct
|
320 videos|1013 docs|210 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Rotational Motion - Physics for JEE Main & Advanced
| 1. What is the significance of rotational motion in JEE Advanced exams? |  |
| 2. How can I prepare effectively for rotational motion questions in JEE Advanced? |  |
| 3. What are some common types of questions asked in rotational motion for JEE Advanced? |  |
| 4. Can you provide a real-life application of rotational motion concepts in JEE? |  |
| 5. Are there any specific formulas I should memorize for rotational motion in JEE Advanced? |  |
















