JEE Advanced Previous Year Questions (2018 - 2023): Properties of Matter | Physics for JEE Main & Advanced PDF Download
2023
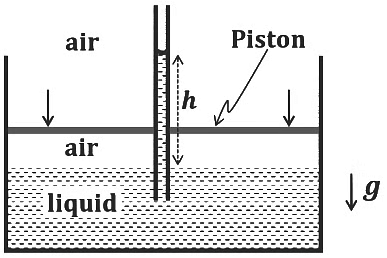
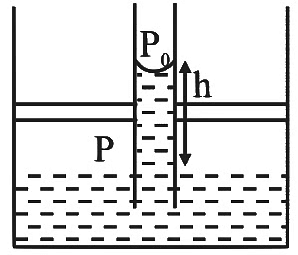
Q1: An incompressible liquid is kept in a container having a weightless piston with a hole. A capillary tube of inner radius 0.1 mm is dipped vertically into the liquid through the airtight piston hole, as shown in the figure. The air in the container is isothermally compressed from its original volume V0 to 100/101 V0 with the movable piston. Considering air as an ideal gas, the height (ℎ) of the liquid column in the capillary above the liquid level in cm is _______.
[Given: Surface tension of the liquid is 0.075 N m−1, atmospheric pressure is 105 N m−2, acceleration due to gravity (g) is 10 m s−2, density of the liquid is 103 kg m−3 and contact angle of capillary surface with the liquid is zero] [JEE Advanced 2023 Paper 2]
Ans: 25
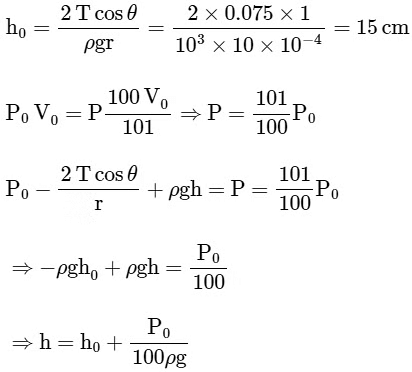
= 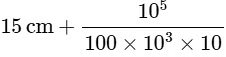
= 25 cm
2022
Q1: A bubble has surface tension S. The ideal gas inside the bubble has ratio of specific heats γ = 5/3. The bubble is exposed to the atmosphere and it always retains its spherical shape. When the atmospheric pressure is Pa1, the radius of the bubble is found to be r1 and the temperature of the enclosed gas is T1. When the atmospheric pressure is Pa2, the radius of the bubble and the temperature of the enclosed gas are r2 and T2, respectively. [JEE Advanced 2022 Paper 2]
Which of the following statement(s) is(are) correct?
(a) If the surface of the bubble is a perfect heat insulator, then  .
.
(b) If the surface of the bubble is a perfect heat insulator, then the total internal energy of the bubble including its surface energy does not change with the external atmospheric pressure.
(c) If the surface of the bubble is a perfect heat conductor and the change in atmospheric temperature is negligible, then 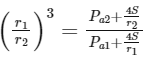 .
.
(d) If the surface of the bubble is a perfect heat insulator, then 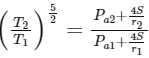 .
.
Ans: (c) & (d)
For adiabatic process:
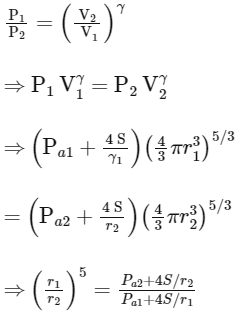
Also, 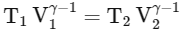
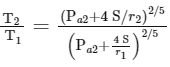
At same temperature,
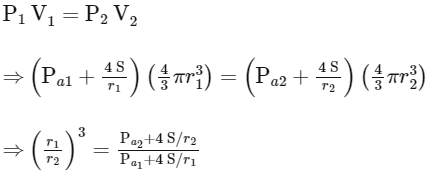
Q2: An ideal gas of density ρ = 0.2 kg m−3 enters a chimney of height ℎ at the rate of α = 0.8 kg s−1 from its lower end, and escapes through the upper end as shown in the figure. The cross-sectional area of the lower end is A1=0.1 m2 and the upper end is A2 = 0.4 m2. The pressure and the temperature of the gas at the lower end are 600 Pa and 300 K, respectively, while its temperature at the upper end is 150 K. The chimney is heat insulated so that the gas undergoes adiabatic expansion. Take g = 10 m s−2 and the ratio of specific heats of the gas γ = 2. Ignore atmospheric pressure.
Which of the following statement(s) is(are) correct?
(a) The pressure of the gas at the upper end of the chimney is 300 Pa.
(b) The velocity of the gas at the lower end of the chimney is 40 m s−1 and at the upper end is 20 ms−1.
(c) The height of the chimney is 590 m.
(d) The density of the gas at the upper end is 0.05 kg m−3. [JEE Advanced 2022 Paper 1]
Ans: (b)
Given g = 10 m s−2 and the ratio of specific heats of the gas γ = 2
The process described is adiabatic. In an adiabatic process (a process during which no heat is gained or lost), the following relationship holds:
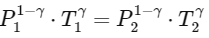
Where :
- P1 and P2 are the initial and final pressures,
- T1 and T2 are the initial and final temperatures,
- γ is the ratio of specific heats (given as 2).
Given that, 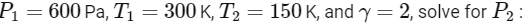

Using the ideal gas law in the form ρ = PM/RT (where R is the specific gas constant), and rearranging to find the relationship between ρ1 and ρ2 :
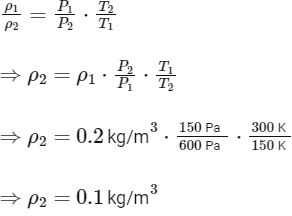
Next, use the principle of conservation of mass flow rate to determine the velocity of the gas at the lower and upper ends.
Similarly, for the upper end :

Work done on the gas = total energy = ΔK + ΔU + internal energy
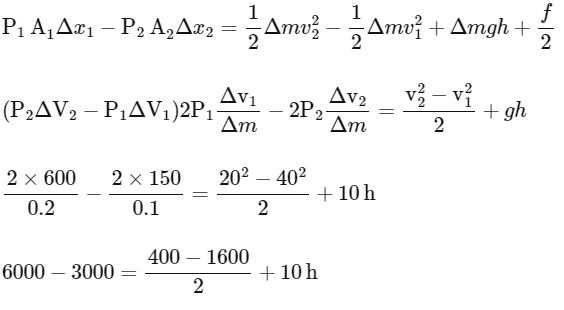
3000 = -600 + 10 h
10h = 3000 + 600
h = 360 m
2021
Q1: A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration a along a fixed inclined plane with angle θ = 45∘. P1 and P2 are pressures at points 1 and 2, respectively, located at the base of the tube. Let β = (P1 − P2)/(ρgd), where ρ is density of water, d is the inner diameter of the tube and g is the acceleration due to gravity. Which of the following statement(s) is(are) correct?
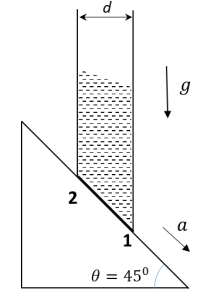 (a)
(a) 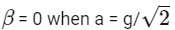
(b) 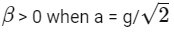
(c) 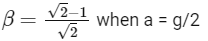
(d)  [JEE Advanced 2021 Paper 1]
[JEE Advanced 2021 Paper 1]
Ans: (a) & (c)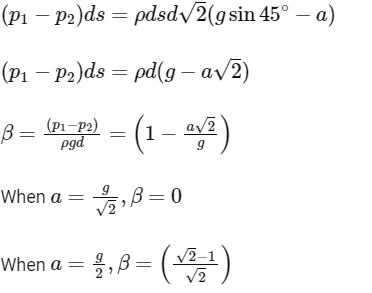
2020
Q1: A train with cross-sectional area St is moving with speed vt inside a long tunnel of cross-sectional area S0 (S0 = 4St). Assume that almost all the air (density ρ) in front of the train flows back between its sides and the walls of the tunnel. Also, the air flow with respect to the train is steady and laminar. Take the ambient pressure and that inside the train to be p0. If the pressure in the region between the sides of the train and the tunnel walls is p, then
p0 - p =
 . The value of 𝑁 is ________. [JEE Advanced 2020 Paper 2]
. The value of 𝑁 is ________. [JEE Advanced 2020 Paper 2]Ans: 9

Applying Bernoulli's equation,

From equation of continuity,
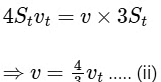
From Eqs. (i) and (ii), we get

∴ N = 9
Q2: A hot air balloon is carrying some passengers, and a few sandbags of mass 1 kg each so that its total mass is 480 kg. Its effective volume giving the balloon its buoyancy is V. The balloon is floating at an equilibrium height of 100 m. When N number of sandbags are thrown out, the balloon rises to a new equilibrium height close to 150 m with its volume V remaining unchanged. If the variation of the density of air with height h from the ground is 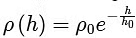 , where ρ0 = 1.25 kg m−3 and h0 = 6000 m, the value of N is _________. [JEE Advanced 2020 Paper 2]
, where ρ0 = 1.25 kg m−3 and h0 = 6000 m, the value of N is _________. [JEE Advanced 2020 Paper 2]
Ans: 4
Weight = Upthrust
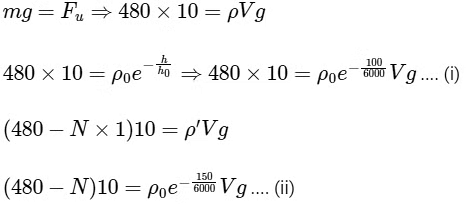
Dividing Eq. (i) by Eq. (ii), we get

N = 4
Q3: A cubical solid aluminium (bulk modulus = 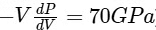 ) block has an edge length of 1 m on the surface of the earth. It is kept on the floor of a 5 km deep ocean. Taking the average density of water and the acceleration due to gravity to be 103 kg m-3 and 10 ms-2, respectively, the change in the edge length of the block in mm is _______. [JEE Advanced 2020 Paper 2]
) block has an edge length of 1 m on the surface of the earth. It is kept on the floor of a 5 km deep ocean. Taking the average density of water and the acceleration due to gravity to be 103 kg m-3 and 10 ms-2, respectively, the change in the edge length of the block in mm is _______. [JEE Advanced 2020 Paper 2]
Ans: 0.24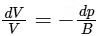 (where, B = bulk modulus)
(where, B = bulk modulus)
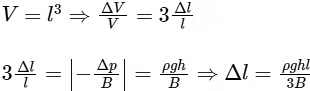
Substituting the given values, we get Δl = 0.24 mm
Q4: When water is filled carefully in a glass, one can fill it to a height h above the rim of the glass due to the surface tension of water. To calculate h just before water starts flowing, model the shape of the water above the rim as a disc of thickness h having semicircular edges, as shown schematically in the figure. When the pressure of water at the bottom of this disc exceeds what can be withstood due to the surface tension, the water surface breaks near the rim and water starts flowing from there. If the density of water, its surface tension and the acceleration due to gravity are 103 kg m−3 , 0.07 Nm−1 and 10 ms−2 , respectively, the value of h (in mm) is _________.
[JEE Advanced 2020 Paper 1]
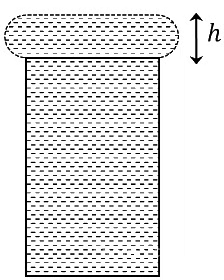 Ans: 3.74
Ans: 3.74

Pressure at the bottom of disc = Pressure due to surface tension

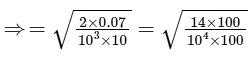
h = √14 mm = 3.741
Q4: An open-ended U-tube of uniform cross-sectional area contains water (density 103 kg m−3 ). Initially the water level stands at 0.29 m from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density 800 kg m−3 is added to the left arm until its length is 0.1 m, as shown in the schematic figure below. The ratio (ℎ1/ℎ2) of the heights of the liquid in the two arms is :
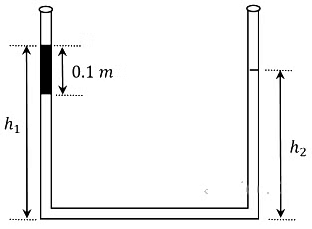 (a) 15/14
(a) 15/14
(b) 35/33
(c) 7/6
(d) 5/4 [JEE Advanced 2020 Paper 1]
Ans: (b)
We have, h1 + h2 = 0.29 × 2 + 0.1
h1 + h2 = 0.68 .......(i)
⇒ p0 + ρkg(0.1) +ρwg(h1 − 0.1) − ρwgh2 = p0
where, ρk = density of kerosene and ρw = density of water.
⇒ ρkg(0.1) + ρwgh1 − ρwg × (0.1) = ρwgh2
⇒ 800 × 10 × 0.1 + 1000 × 10 × h1 − 1000 × 10 × 0.1 = 1000 × 10 × h2
⇒ 10000(h1 − h2) = 200
⇒ h1 − h2 = 0.01 .......(ii)
Solving Eqs. (i) and (ii), we get
h1 = 0.35
and h2 = 0.33
So, h1 / h2 = 35/33
2019
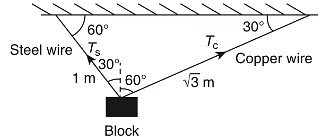
Q1: A block of weight 100 N is suspended by copper and steel wires of same cross-sectional area 0.5 cm2 and length √3 m and 1 m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘ and 60∘, respectively. If elongation in copper wire is (Δlc) and elongation in steel wire is (Δls), then the ratio Δlc / Δls is .............. .
[Young's modulus for copper and steel are 1 × 1011 N/m2 and 2 × 1011 N/m2 respectively.] [JEE Advanced 2019 Paper 1]
 Ans: 2
Ans: 2

= 2.00
Q2: A liquid at 30∘C is poured very slowly into a Calorimeter that is at temperature of 110∘C. The boiling temperature of the liquid is 80∘C. It is found that the first 5 gm of the liquid completely evaporates. After pouring another 80 gm of the liquid the equilibrium temperature is found to be 50∘C. The ratio of the latent heat of the liquid to its specific heat will be ...........∘C.
[Neglect the heat exchange with surrounding] [JEE Advanced 2019 Paper 1]
Ans: 270
Case - I 5C × 50 + 5L = C2 × 30 ....(i)
Case - II 80C[50 − 30] = C2 [80 − 50] ....(ii)
By Eq. (i) and (ii)
1600C = 250 + 5L 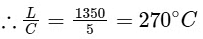
Q3: A current carrying wire heats a metal rod. The wire provides a constant power (P) to the rod. The metal rod is enclosed in an insulated container. It is observed that the temperature (T) in the metal rod changes with time (t) as 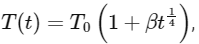 where β is a constant with appropriate dimension while T0 is a constant with dimension of temperature. The heat capacity of the metal is
where β is a constant with appropriate dimension while T0 is a constant with dimension of temperature. The heat capacity of the metal is
(a) 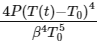
(b) 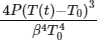
(c) 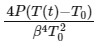
(d) 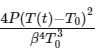 [JEE Advanced 2019 Paper 1 ]
[JEE Advanced 2019 Paper 1 ]
Ans: (b)
Heat Capacity, 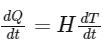
Power of the rod, 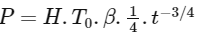
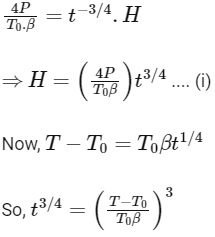
Substituting this value of t3/4 in equation (i) we get,
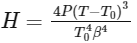
2018
Q1: Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures T1 = 300K and T2 = 100K, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller once and the thermal conductivities of the materials of the smaller and the larger cylinders are K1 and K2 respectively. If the temperature at the junction of the two cylinders in the steady state is 200 K, then K1/K2= ______________. [JEE Advanced 2018 Paper 1]
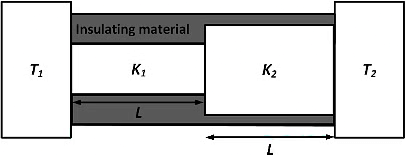 Ans: 4
Ans: 4
The intermediate temperature is given by the formula
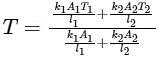
Here, T = 200 k, T1 = 300 k, T2 = 100 k, l1 = l2 and A1 = πr2, A2 = 4πr2
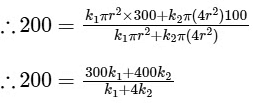
∴ 200 k1 + 800 k2 = 300 k1 + 400 k
⇒ 400 k2 = 100 k1
∴ k1 / k2 = 4.0
Q2: Consider a thin square plate floating on a viscous liquid in a large tank. The height ℎ of the liquid in the tank is much less than the width of the tank. The floating place is pulled horizontally with a constant velocity μ0. Which of the following statements is (are) true? [JEE Advanced 2018 Paper 2]
(a) The resistive force of liquid on the plate is inversely proportional to ℎ
(b) The resistive force of liquid on the plate is independent of the area of the plate
(c) The tangential (shear) stress on the floor of the tank increases with μ0
(d) The tangential (shear) stress on the plate varies linearly with the viscosity η of the liquid
Ans: (c) & (d)
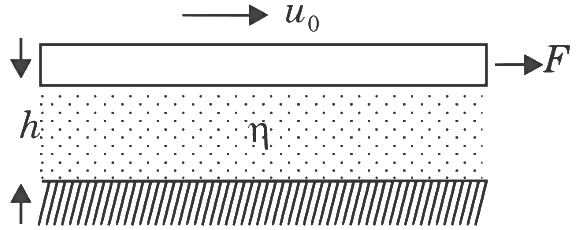 Force of viscosity can be written as follows:
Force of viscosity can be written as follows: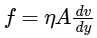
Here η is coefficient of viscosity, A is face area of plate and dv / dy is velocity gradient. We can assume that velocity of fluid at the bottom (h depth below) is zero; hence 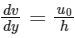 ; hence force of viscocity can be written as follows:
; hence force of viscocity can be written as follows: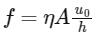
We can see that force of viscosity is inversely proportional to h; hence option (a) is correct.
We can see that force of viscosity is proportional to area of plate; hence option (b) is wrong.
Tangential stress can be written as 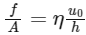
We can see that options (c) and (d) are also correct.
Q3: A uniform capillary tube of inner radius r is dipped vertically into a beaker filled with water. The water rises to a height ℎ in the capillary tube above the water surface in the beaker. The surface tension of water is σ. The angle of contact between water and the wall of the capillary tube is θ. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
(a) For a given material of the capillary tube, ℎ decreases with increase in r
(b) For a given material of the capillary tube, ℎ is independent of σ
(c) If this experiment is performed in a lift going up with a constant acceleration, then ℎ decreases
(d) ℎ is proportional to contact angle θ [JEE Advanced 2018 Paper 1]
Ans: (a) & (c)
We know that,
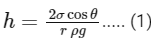
where r is inner radius of capillary tube; σ is surface tension; θ is angle between water and wall of capillary tube; h is height of water in capillary tube and g is acceleration due to gravity. From Eq. (1),

Therefore, for a given material of the capillary tube, h decreases with increase in r.
Hence, option (A) is correct.
h depends on σ, therefore option (B) is incorrect.
In a lift going up with a constant acceleration a, the force due to surface tension remains same but weight of the water increases i.e., Wlift = πr2hρ(g + a). Thus, the height of the water rise in a capillary becomes
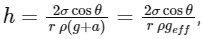
where geff is the effective g in the lift. Hence, h decrease if the experiment is performed in a lift going up with a constant acceleration.
From (1), h ∝ cosθ and not θ, therefore, option (D) is incorrect.
|
289 videos|635 docs|179 tests
|

|
Explore Courses for JEE exam
|

|
















