JEE Advanced Previous Year Questions (2018 - 2023): Sets, Relations and Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download

2023

Let domain and co-domain of a function y = f(x) are S and T respectively.
(A) There are infinitely many elements in domain and four elements in co-domain.
⇒ There are infinitely many functions from S to T.
⇒ Option (A) is correct
(B) If number of elements in domain is greater than number of elements in co-domain, then number of strictly increasing function is zero.
⇒ Option (B) is incorrect
(C) Maximum number of continuous functions = 4 × 4 × 4 = 64
(Every subset (0, 1),(1, 2),(3, 4) has four choices)
∵ 64<120⇒ option (C) is correct.
(D) For every point at which f(x) is continuous, f(x) = 0
⇒ Every continuous function from S to T is differentiable.
Option (D) is correct. 

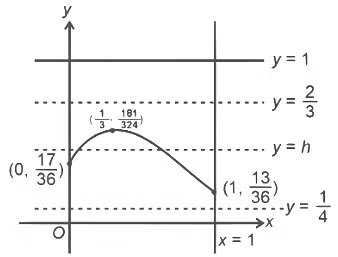
Q2: Let f : [0, 1] → [0, 1] be the function defined by 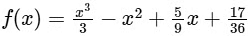. Consider the square region S = [0, 1] × [0, 1]. Let  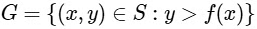be called the green region and  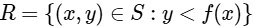be called the red region. Let  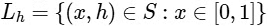be the horizontal line drawn at a height ℎ ∈ [0, 1]. Then which of the following statements is(are) true? 
(a) There exists an ℎ ∈ [1/4, 2/3] such that the area of the green region above the line L_ℎ equals the area of the green region below the line L_ℎ
(b) There exists an ℎ ∈ [1/4, 2/3] such that the area of the red region above the line L_ℎ equals the area of the red region below the line L_ℎ
(c) There exists an ℎ ∈ [1/4, 2/3] such that the area of the green region above the line L_ℎ equals the area of the red region below the line L_ℎ
(d) There exists an ℎ ∈ [1/4, 2/3] such that the area of the red region above the line L_ℎ equals the area of the green region below the line                   [JEE Advanced 2023 Paper 1]
Ans: (b), (c) & (d)
Given,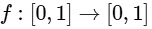

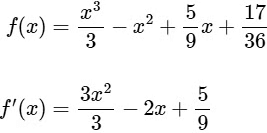
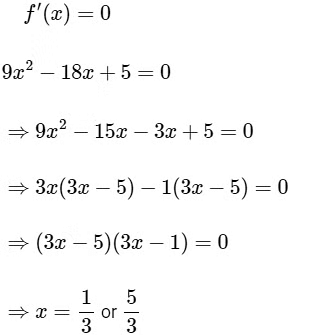
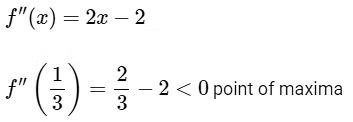
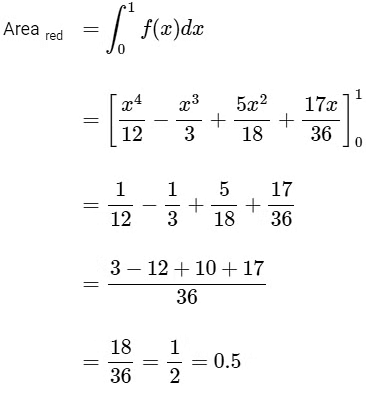
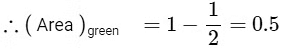
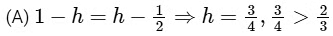 option (A) is incorrect

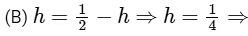 option (B) is correct.

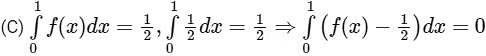
⇒ h= 1/2 ⇒ option (C) is correct.
(D) ∵ Option (C) is correct ⇒ option (D) is also correct.

2022

Q1: Let |M| denote the determinant of a square matrix M. Let 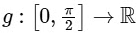 be the function defined by 

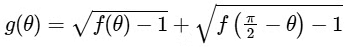
where

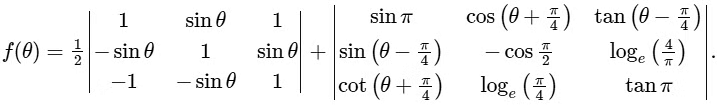
Let p(x) be a quadratic polynomial whose roots are the maximum and minimum values of the function g(θ), and p(2)  =2 − √2. Then, which of the following is/are TRUE ? 
(a)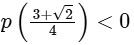
(b)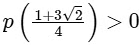
(c)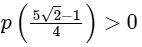
(d) 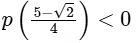            [JEE Advanced 2022 Paper 1]Ans: (a) & (c)
Given,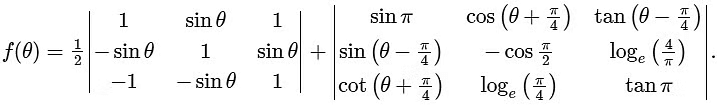

Here,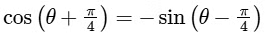

and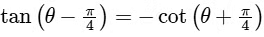

and

Also,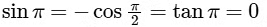

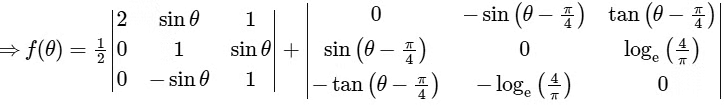
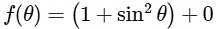  (skew symmetric)  

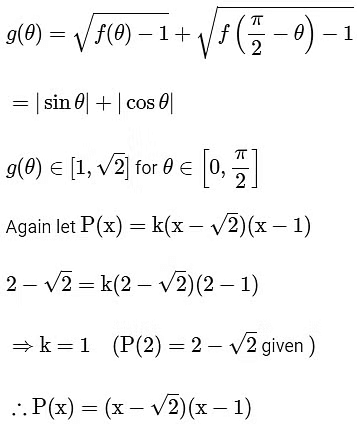
For option (A)  Correct.
For option (B) 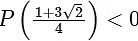 Incorrect.
For option (C)  Correct.
For option (D) 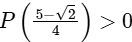 Incorrect. 

2020

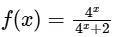Then the value of  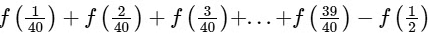is .......... 
Ans: 19
The given function f : [0, 1] → R be define by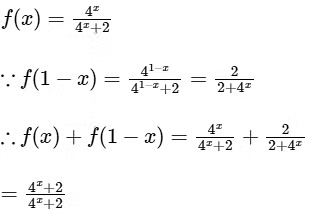

So, f(x) + f(1 − x) = 1 .....(i)

=

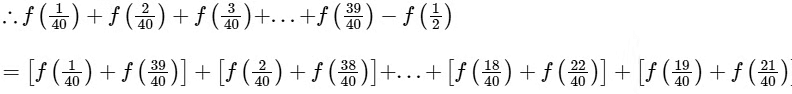
=  (19 times) {from Eq. (i)}
= 19. 

Q2: Let the function be defined by 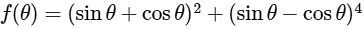Suppose the function f has a local minimum at θ precisely when 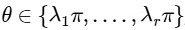, where 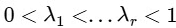. Then the value of  is .............     [JEE Advanced 2020 Paper 2]
Ans: 0.5
The given function f : R → R be defined by

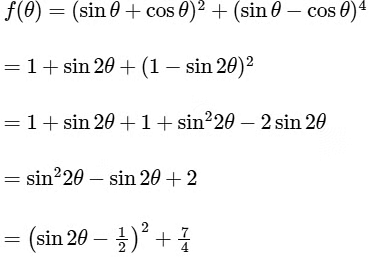
The local minimum of function 'f' occurs when

but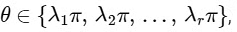

Where,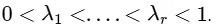

So, 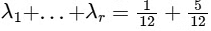 = 0.50

Q3: Let f : [0, 2] → R be the function defined by

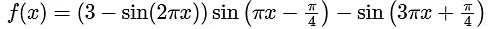
If 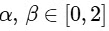 are such that 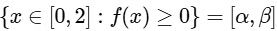, then the value of β - α is ..........     [JEE Advanced 2020 Paper 1]
Ans: 1
The given function f : [0, 2] → R defined by

As, 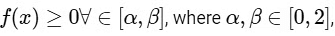so,

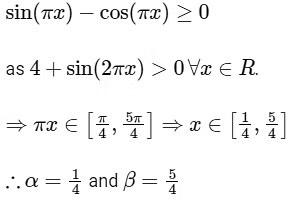
Therefore the value of (β - α) = 1

Q3: For a polynomial g(x) with real coefficients, let m_g denote the number of distinct real roots of g(x). Suppose S is the set of polynomials with real coefficients defined by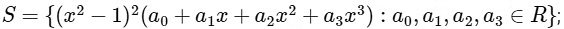
For a polynomial f, let f' and f'' denote its first and second order derivatives, respectively. Then the minimum possible value of (m_f' + m_f''), where f ∈ S, is ..............     [JEE Advanced 2020 Paper 1]
Ans: 5
Given set S of polynomials with real coefficients

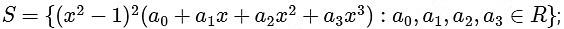
and for a polynomial f ∈ S, Let

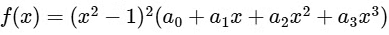it have −1 and 1 as repeated roots twice, so graph of f(x) touches the X-axis at x = −1 and x = 1, so f'(x) having at least three roots x = −1, 1 and α. Where α ∈ (−1, 1) and f''(x) having at least two roots in interval (−1, 1)
So, m_f' = 3 and m_f'' = 2
∴ Minimum possible value of (m_f' + m_f'') = 5 

Q4: If the function f : R → R is defined by f(x) = |x| (x − sin x), then which of the following statements is TRUE?
(a) f is one-one, but NOT onto
(b) f is onto, but NOT one-one
(c) f is BOTH one-one and onto
(d) f is NEITHER one-one NOR onto             [JEE Advanced 2020 Paper 1]
Ans: (c)
The given function f : R → R is

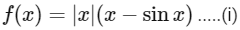
The function 'f' is a odd and continuous function and as 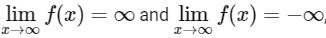, so range is R, therefore, 'f' is a onto function.

⇒ f is strictly increasing function. ∀x ∈(0, ∞).
Similarly, for x < 0, −x + sin x > 0 and (− x) (1 − cos x) > 0, therefore, f′(x)> 0∀ x ∈(−∞, 0)
⇒ f is strictly increasing function, ∀x ∈ (0, ∞)
Therefore 'f' is a strictly increasing function for x ∈ R and it implies that f is one-one function. 

2018

Q1: Let X be a set with exactly 5 elements and Y be a set with exactly 7 elements. If α is the number of one-one functions from X to Y and β is the number of onto functions from Y to X, then the value of 1 / 5!(β − α) is ..................                  [JEE Advanced 2018 Paper 2]
Ans: 119
Given, X has exactly 5 elements and Y has exactly 7 elements.
∴ n(X) = 5
and n(Y) = 7
Now, number of one-one functions from X to Y is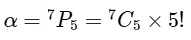
Number of onto functions from Y to X is  β

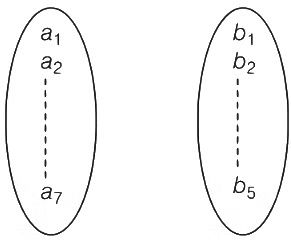
1, 1, 1, 1, 3 or 1, 1, 1, 2, 2

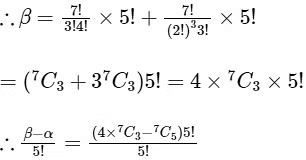= 4 x 35 - 21= 140 - 21
= 119

Q2: Let 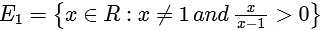 and 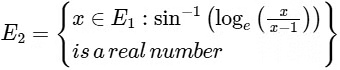(Here, the inverse trigonometric function sin⁻¹ x assumes values in [−π/2, π/2].). 
Let f : E₁ → R be the function defined by 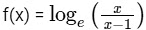 and g : E₂ → R be the function defined by  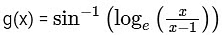.      [JEE Advanced 2018 Paper 2]

The correct option is :
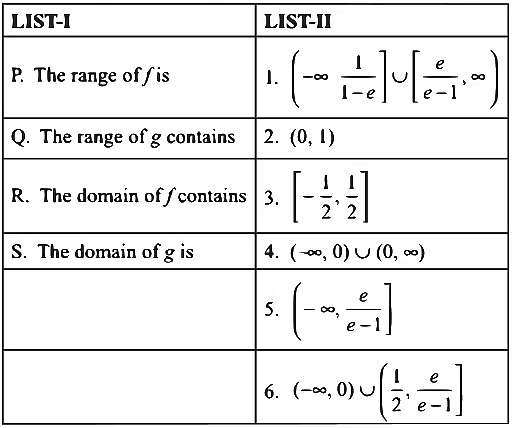
(a) P → 4; Q → 2; R → 1 ; S → 1
(b) P → 3; Q → 3; R → 6 ; S → 5
(c) P → 4; Q → 2; R → 1 ; S → 6
(d) P → 4; Q → 3; R → 6 ; S → 5                  [JEE Advanced 2018 Paper 2]
Ans: (a)
We have,

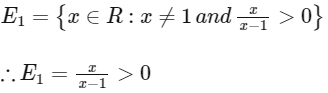
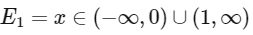
and

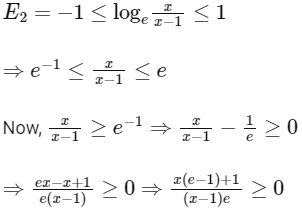
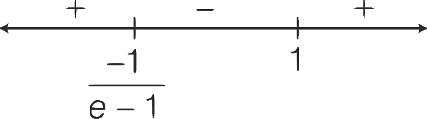
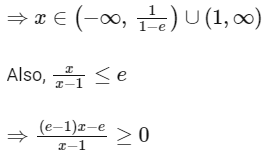
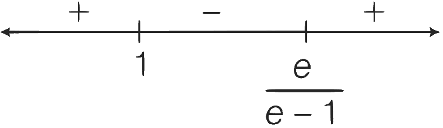
So,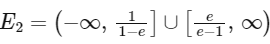

The domain of f and g are  
and Range of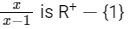

Range of f is R − {0} or (−∞, 0) ∪ (0, ∞) 
Range of g is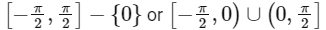
Now, P → 4, Q → 2, R → 1, S → 1 
Hence, option (a) is correct answer.