JEE Advanced Previous Year Questions (2018 - 2023): Circle | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let A1, A2, A3, …, A8 be the vertices of a regular octagon that lie on a circle of radius 2 . Let P be a point on the circle and let PAi denote the distance between the points P and Ai for i = 1 ,2,…,8. If P varies over the circle, then the maximum value of the product PA1 × PA2 × ⋯⋯ × PA8, is : [JEE Advanced 2023 Paper 2]
Ans: 512
Q2: Let C1 be the circle of radius 1 with center at the origin. Let C2 be the circle of radius r with center at the point A = (4, 1), where 1< r <3. Two distinct common tangents PQ and ST of C1 and C2 are drawn. The tangent PQ touches C1 at P and C2 at Q. The tangent ST touches C1 at S and C2 at T. Mid points of the line segments PQ and ST are joined to form a line which meets the x-axis at a point B. If AB = √5, then the value of r2 is : [JEE Advanced 2023 Paper 2]
Ans: 2
Q3: Consider an obtuse angled triangle ABC in which the difference between the largest and the smallest angle is π/2 and whose sides are in arithmetic progression. Suppose that the vertices of this triangle lie on a circle of radius 1.
Let be the area of the triangle . Then the value of is Let a be the area of the triangle ABC. Then the value of (64a)2 is : [JEE Advanced 2023 Paper 2]
Ans: 1008
Q4: Consider an obtuse angled triangle ABC in which the difference between the largest and the smallest angle is π/2 and whose sides are in arithmetic progression. Suppose that the vertices of this triangle lie on a circle of radius 1.
Then the inradius of the triangle ABC is : [JEE Advanced 2023 Paper 2]
Ans: 0.25
2022
Q1: Let ABC be the triangle with AB = 1, AC=3 and ∠BAC = π/2. If a circle of radius r > 0 touches the sides AB, AC and also touches internally the circumcircle of the triangle ABC, then the value of r is __________ . [JEE Advanced 2022 Paper 1]
Ans: 0.82 to 0.86
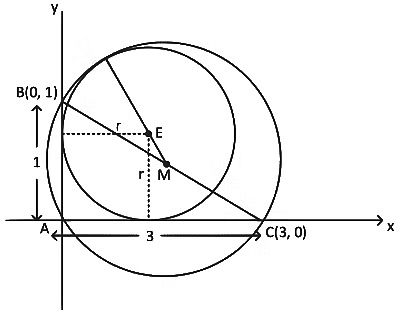
Here ABC is a right angle triangle. BC is the Hypotenuse of the triangle.
We know, diameter of circumcircle of a right angle triangle is equal to the Hypotenuse of the triangle also midpoint of Hypotenuse is the center of circle.
∴ BC = Diameter of the circle
Here B = (0, 1) and C (3, 0)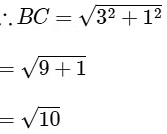
∴ Radius of circumcircle (R) = √10/2
∴ Center of circle (M) = 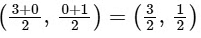
Center of circle which touches line AB and AC = (r, r)
Now distance between center of two circles,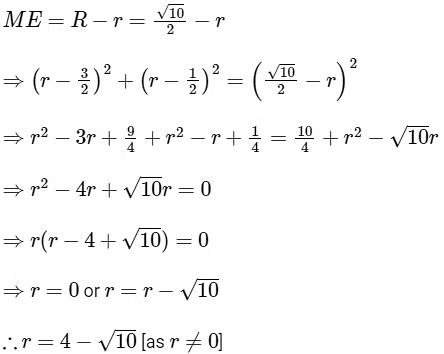
= 0.837≅ 0.84
2021
Q1: Consider the region R = {(x, y) ∈ R × R : x ≥ 0 and y2 ≤ 4 − x}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F. Let (α, β) be a point where the circle C meets the curve y2 = 4 − x.
The radius of the circle C is ___________. [JEE Advanced 2021 Paper 2]
Ans: 1.50
Given, x ≥ 0, y2 ≤ 4 − x
Let equation of circle be
(x − h)2 + y2 = h2 .... (i)
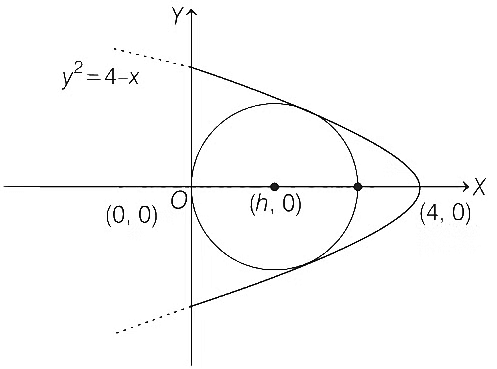
Solving Eq. (i) with y2 = 4 − x, we get
x2 − 2hx + 4 − x = 0
⇒ x2 − x(2h + 1) + 4 = 0 .... (ii)
For touching/tangency, Discriminant (D) = 0
i.e. (2h + 1)2 = 16
⇒ 2h + 1 = ± 4
⇒ 2h = ± 4 − 1
⇒ ℎ = 3/2, ℎ = −5/2 (Rejected) because part of circle lies outside R.
So, ℎ = 3/2 = radius of circle (C).
Q2: Consider the region R = {(x, y) ∈ R × R : x ≥ 0 and y2 ≤ 4 − x}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F. Let (α, β) be a point where the circle C meets the curve y2 = 4 − x.
The value of α is ___________. [JEE Advanced 2021 Paper 2]
Ans: 2.00
Given, x ≥ 0, y2 ≤ 4 − x
Let equation of circle be
(x − h)2 + y2 = h2 .... (i) 2
Solving Eq. (i) with y2 = 4 − x, we get
x2 − 2hx + 4 − x = 0
⇒ x2 − x(2h + 1) + 4 = 0 .... (ii)
For touching/tangency, Discriminant (D) = 0
i.e. (2h + 1)2 = 16
⇒ 2h + 1 = ± 4
⇒ 2h = ± 4 − 1
⇒ ℎ = 3/2, ℎ = −5/2 (Rejected) because part of circle lies outside R.
So, ℎ = 3/2 = radius of circle (C).
Putting h = 3/2 in Eq. (ii),
x2 − 4x + 4 = 0
⇒ (x − 2)2 = 0
⇒ x = 2
So, α = 2
Q3: Let 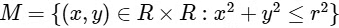 , where r > 0. Consider the geometric progression
, where r > 0. Consider the geometric progression 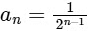 , n = 1, 2, 3, ...... . Let S0 = 0 and for n ≥ 1, let Sn denote the sum of the first n terms of this progression. For n ≥ 1, let Cn denote the circle with center (Sn−1, 0) and radius an, and Dn denote the circle with center (Sn−1, Sn−1) and radius an.
, n = 1, 2, 3, ...... . Let S0 = 0 and for n ≥ 1, let Sn denote the sum of the first n terms of this progression. For n ≥ 1, let Cn denote the circle with center (Sn−1, 0) and radius an, and Dn denote the circle with center (Sn−1, Sn−1) and radius an.
Consider M with r = 1025 / 513. Let k be the number of all those circles Cn that are inside M. Let l be the maximum possible number of circles among these k circles such that no two circles intersect. Then
(a) k + 2l = 22
(b) 2k + l = 26
(c) 2k + 3l = 34
(d) 3k + 2l = 40 [JEE Advanced 2021 Paper 2]
Ans: (d)
For circle Cn to be inside M.
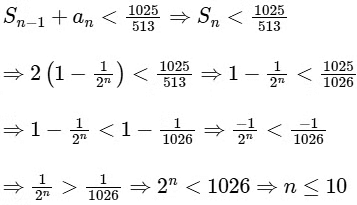
∴ Number of circles inside be 10 = k. Clearly, alternate circle do not intersect each other i.e. C1, C3, C5, C7, C9 do not intersect each other as well as C2, C4, C6, C8 and C10 do not intersect each other.
Hence, maximum 5 set of circles do not intersect each other.
∴ l = 5
So, 3k + 2l = 40
Q4: Let 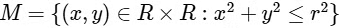 , where r > 0. Consider the geometric progression
, where r > 0. Consider the geometric progression 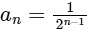 , n = 1, 2, 3, ...... . Let S0 = 0 and for n ≥ 1, let Sn denote the sum of the first n terms of this progression. For n ≥ 1, let Cn denote the circle with center (Sn−1, 0) and radius an, and Dn denote the circle with center (Sn−1, Sn−1) and radius an.
, n = 1, 2, 3, ...... . Let S0 = 0 and for n ≥ 1, let Sn denote the sum of the first n terms of this progression. For n ≥ 1, let Cn denote the circle with center (Sn−1, 0) and radius an, and Dn denote the circle with center (Sn−1, Sn−1) and radius an.
Consider M with 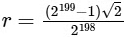 . The number of all those circles Dn that are inside M is
. The number of all those circles Dn that are inside M is
(a) 198
(b) 199
(c) 200
(d) 201 [JEE Advanced 2021 Paper 2]
Ans: (b)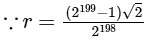
Now, 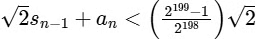
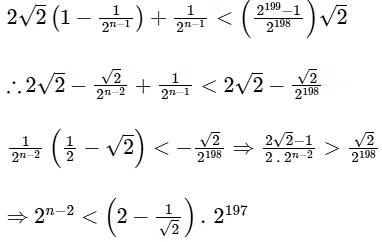
n ≤ 199
So, number of circles = 199
Q5: Consider a triangle Δ whose two sides lie on the x-axis and the line x + y + 1 = 0. If the orthocenter of Δ is (1, 1), then the equation of the circle passing through the vertices of the triangle Δ is [JEE Advanced 2021 Paper 1]
(a) x2 + y2 − 3x + y = 0
(b) x2 + y2 + x + 3y = 0
(c) x2 + y2 + 2y − 1 = 0
(d) x2 + y2 + x + y = 0
Ans: (b)
Equation of circle passing through C(0, 0) is
x2 + y2 + 2gx + 2fy = 0 ..... (i)
Since Eq. (i), also passes through (−1, 0) and (1, −2).
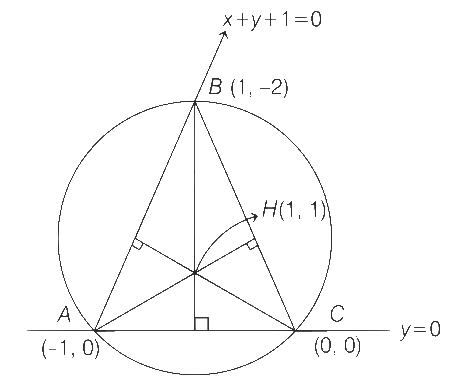
Then, 1 − 2g = 0
⇒ g = 1 / 2
and 5 + 1 − 4f = 0
⇒ f = 3 / 2
∴ Equation of circumcircle is
x2 + y2 + 2 × 1/2x + 2 × 3/2y = 0
i.e. x2 + y2 + x + 3y = 0
2020
Q1: Let O be the centre of the circle x2 + y2 = r2, where r > √5/2. Suppose PQ is a chord of this circle and the equation of the line passing through P and Q is 2x + 4y = 5. If the centre of the circumcircle of the triangle OPQ lies on the line x + 2y = 4, then the value of r is ............. [JEE Advanced 2020 Paper 2]
Ans: 2
As we know that the equation of family of circles passes through the points of intersection of given circle x2 + y2 = r2 and line PQ : 2x + 4y = 5 is,
(x2 + y2 − r2) + λ(2x + 4y − 5) = 0 ......(i)
Since, the circle (i) passes through the centre of circle
x2 + y2 = r2,
So, − r2 − 5λ = 0
or 5λ + r2 = 0 ....(ii)
and the centre of circle (i) lies on the line x + 2y = 4, so centre (− λ, − 2λ) satisfy the line x + 2y = 4.
Therefore, −λ − 4λ = 4
⇒ −5λ = 4
⇒ r2 = 4 {from Eq. (ii)}
⇒ r = 2
2019
Q1: Let the point B be the reflection of the point A(2, 3) with respect to the line 8x − 6y − 23 = 0. Let ΓA and ΓB be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles ΓA and ΓB such that both the circles are on the same side of T. If C is the point of intersection of T and the line passing through A and B, then the length of the line segment AC is ................. [JEE Advanced 2019 Paper 1]
Ans: 10
According to given information the figure is as following
From the figure,
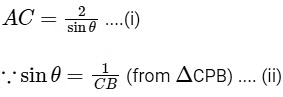
and 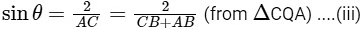
∵ AB = AM + MB = 2AM [∵ AM = MB] 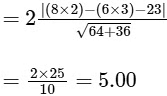
From Eqs. (ii) and (iii), we get
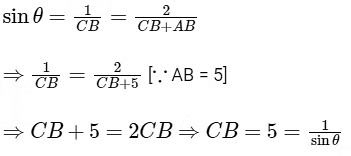
From the Eq. (i), we get
AC = 2/sinθ = 2 x 5 = 10
Q2: A line y = mx + 1 intersects the circle (x − 3)2 + (y + 2)2 = 25 at the points P and Q. If the midpoint of the line segment PQ has x-coordinate −3/5, then which one of the following options is correct?
(a) 6 ≤ m < 8
(b) −3 ≤ m < −1
(c) 4 ≤ m < 6
(d) 2 ≤ m < 4 [JEE Advanced 2019 Paper 1]
Ans: (d)
It is given that points P and Q are intersecting points of circle (x − 3)2 + (y + 2)2 = 25 .....(i)
Line y = mx + 1 .....(ii)
And, the mid-point of PQ is A having x-coordinate −3 / 5
so y-coordinate is 1 − 3 / 5 m.
So, 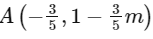
From the figure,
∵ AC ⊥ PQ 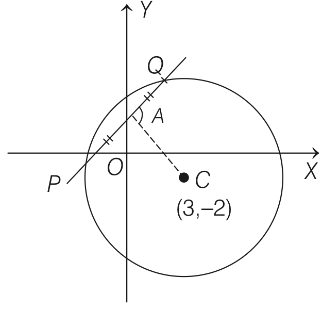
⇒ (slope of AC) × (slope of PQ) = −1 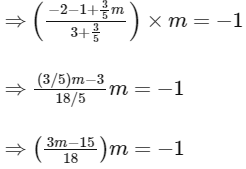
⇒ 3m2 - 15m + 18 = 0
⇒ m2 - 5m + 6 = 0
⇒ m = 2 or 3
|
209 videos|443 docs|143 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2023): Circle - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the importance of JEE Advanced in the admission process for engineering colleges in India? |  |
| 2. How can I prepare for JEE Advanced effectively? |  |
| 3. Can I appear for JEE Advanced without qualifying JEE Main? |  |
| 4. What is the marking scheme for JEE Advanced? |  |
| 5. Can I use a calculator in the JEE Advanced exam? |  |
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|

















