Solved Examples on Methods of Integration | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| Method of Substitution |

|
| Trigonometric Integrals |

|
| Trigonometric Substitutions |

|
| Completing the Square |

|
| Integration by Parts |

|
Method of Substitution
Example 1: Find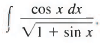
Sol: Here we notice that cos x dx is the differential of sin x, and also of 1 + sin x. Thus, if we put u = 1 + sin x, then du = cos x dx and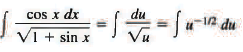
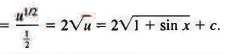
Example 2: Find
Sol: Since 4x2 = (2x)2 we put u = 2x, so that du = 2dx, dx = 1/2 du , and
Example 3: Find
Sol: Here the fact that the x in the numerator is essentially the derivative of the expression 9 - 4x2 inside the radical suggests the substitution u = 9 - 4x2. Then du = - 8x dx, and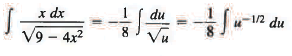

Trigonometric Integrals
Example 4: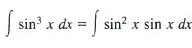
Sol:
Example 5: The half-angle formula for the cosine enables us to write
Sol: 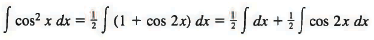
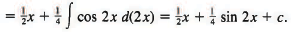
If we wish to express this result in terms of the variable x (instead of 2x), we use the double-angle formula sin 2x = 2 sin x cos x and write
Example 6: By using both of the half-angle formulas we get
Sol: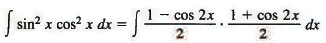
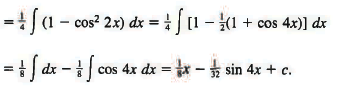
Example 7: ∫tan3 x sec5x dx = ∫ tan2 x sec4 x sec x tan x dx
Sol: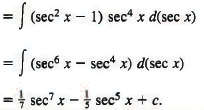
Trigonometric Substitutions
Example 8: Find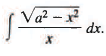
Sol: This integ ral is o f th e first type, so we write
x= a sin θ, dx = a cos θ dθ,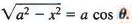
Then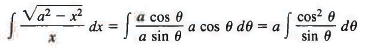
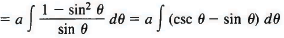
= —a ln (csc θ + cot θ) + a cos θ. ...(7)
This completes the integration, and we now must write the answer in terms of the original variable x. We do this quickly and easily by drawing a right triangle whose sides are labeled in the simplest way that is consistent with the equation x = a sin θ or sin θ = x/a. This figure tellsus at once that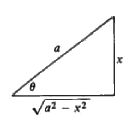
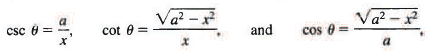
so from (7) we have
Example 9: Find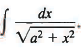
Sol:
x = a tan θ, dx = a sec2 θ dθ,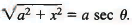
This yields
= ln (sec θ + tan θ) ...(8)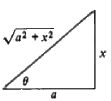 The substitution equation x = a tan 6 or tan 6 = x/a is pictured in Fig, and from this figure we obtain
The substitution equation x = a tan 6 or tan 6 = x/a is pictured in Fig, and from this figure we obtain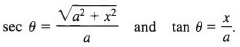
We therefore continue the calculation in (8) by writing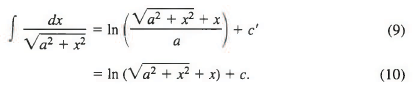
Students will notice that since
the constant -In a has been grouped together with the constant of integration c' and the quantity -In a + c' is then rewritten as c. Usually we don’t bother to make notational distinctions between one constant of integration and another, because all are completely arbitrary; but we do so here in the hope of clarifying the transition from (9) to (10).
Completing the Square
Example 10: Find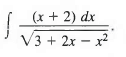
Sol:
Since the coefficient of the term x2 under the radical is negative, we place the terms containing x in parentheses preceded by a minus sign, leaving space for completing the square,
3 + 2x — x2 = 3 — (x2 — 2x + ) = 4 — (x2 — 2x + 1)
= 4 — (x - 1)2 = a2 — u2,
where u = x - 1 and a = 2.
Since x = u + 1, we have dx = du and x + 2 = u + 3, and therefore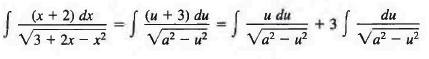
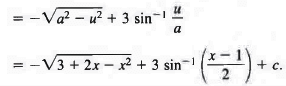
Q11: Find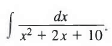
Sol:
We complete the square on the terms containing x, and write
x2 + 2x + 10 = (x2 + 2x + ) + 10 = (x2 + 2x + 1) + 9
= (x + 1)2 + 9 = u2 + a2 ,
where u = x + 1 and a = 3. We now have = dx or d x = du , so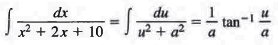
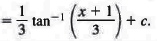
Q12: Find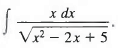
Sol: We write
x2 - 2x + 5 = (x2 — 2x + ) + 5 = (x2 — 2x + 1) + 4
= (x - 1)2 + 4 = u2 + a2 ,
where u = x - 1 and a = 2. Then x = u + 1, dx = du, and we have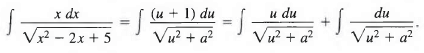
The second integral here is the one considered in Example 2 in Section 10.4, so we have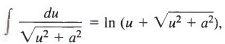
and therefore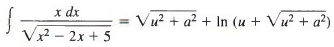
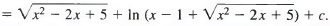
Q13: Find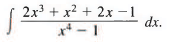
Sol: We have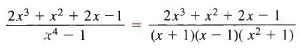
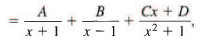
so
2x3 + x2 + 2x - 1 = A (x - 1)(x2 + 1) + 5 (x + 1)(x2 + 1) + Cx(x2 - 1) + D(x2 — 1).
Now put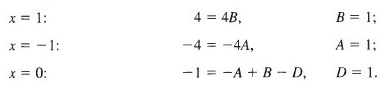
Equating coefficients of x3 gives
2 = A + 5 + C, so C = 0.
Our partial fractions decomposition is therefore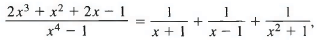
so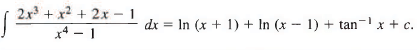
Integration by Parts
Example 14: Find ∫ ln x dx.
Sol: Here our only choice is
w = ln x, dv = dx,
so
and we have
Example 15: Find ∫ x2ex dx.
Sol: If we put
u = x2, dv = ex dx,
then du = 2x dx, v = ex
and (1) gives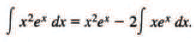 ....(2)
....(2)
Here the second integral is easier than the first, so we are encouraged to continue in the same way. When the second integral is integrated by parts with
u = x, dv = ex dx,
so that
du = dx, v = ex,
then we get
xex - ex.
When this is in serted in (2), our final result is
∫x2ex dx = x2ex - 2xex + 2ex + c.
Example 16: Find ∫ex cos x dx.
Sol: For convenience we denote this integral by J. If we put
u = ex, dv = cos x dx,
then
du = ex dx, v = sin x,
and (1) yields
J = ex sin x - ∫ex sin x dx. .....(3)
Now we come to the interesting part of this problem. Even though the new integral is no easier than the old, it turns out to be fruitful to apply the same method again to the new integral. Thus, we put
u = ex, dv = sin x dx,
so that
du = ex dx, v = -cos x,
and obtain
∫ex sin x dx = -ex cos x + ∫ ex cos x dx. ....(4)
The integral on the right is J again , so (4) can be written
∫ex sin x dx = - ex cos x + J. ......(5)
In spite of appearances, we are not going in a circle, because substituting (5) in (3) gives
J = ex sin x + ex cos x - J.
It is now easy to solve for J by writing
2J = ex sin x + ex cos x or J = 1/2 (ex sin x + ex cos x), and all that remains is to insert the constant of integration:
Exmaple 17: Find a reduction formula for Jn = ∫ sinn x dx.
Sol: We integrate by parts with
u = sinn-1x, dv = sin x dx,
so that du = {n — 1) sinn-2 x cos x dx, v = —cos x,
and therefore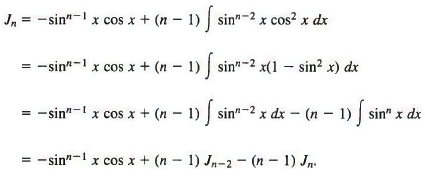
We now transpose the term involving Jn and obtain
nJn = - sinn-1 x cos x + (n - 1)Jn-2,
so that
or equivalently, ....(6)
....(6)
Example 18: Calculate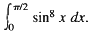
Sol: For convenience we write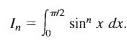
By formula (6) we have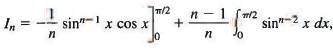
so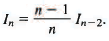
We apply this formula with n = 8, then repeat with n = 6, n = 4, n = 2:
Therefore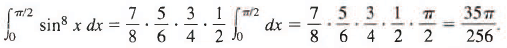
|
289 videos|635 docs|179 tests
|

|
Explore Courses for JEE exam
|

|
















