JEE Advanced Previous Year Questions (2018 - 2023): Sequences and Series | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let  denote the (r + 2) digit number where the first and the last digits are 7 and the remaining r digits are 5 . Consider the sum
denote the (r + 2) digit number where the first and the last digits are 7 and the remaining r digits are 5 . Consider the sum 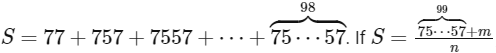 , where m and n are natural numbers less than 3000 , then the value of m + n is: [JEE Advanced 2023 Paper 1]
, where m and n are natural numbers less than 3000 , then the value of m + n is: [JEE Advanced 2023 Paper 1]
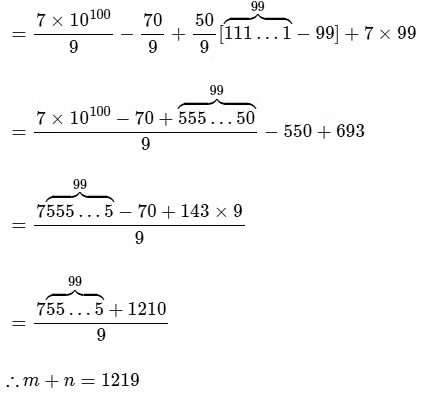
Ans: 1219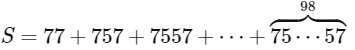
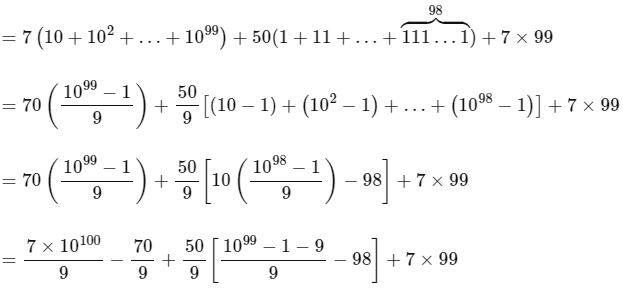
2022
Q1: Let a1, a2, a3,… be an arithmetic progression with a1 = 7 and common difference 8. Let T1, T2, T3,… be such that T1 = 3 and Tn+1 − Tn = an for n ≥ 1. Then, which of the following is/are TRUE ?
(a) T20 = 1604
(b) 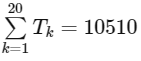
(c) T30 = 3454
(d) 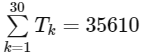 [JEE Advanced 2022 Paper 1]
[JEE Advanced 2022 Paper 1]
Ans: (b) & (c)
Here an = 7 + (n - 1)8 and T1 = 3, a1 = 7, d = 8
Also, Tn+1 = Tn + an
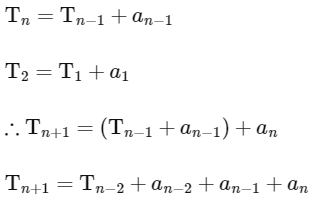
So,
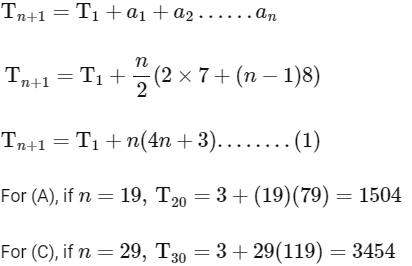
For (B),
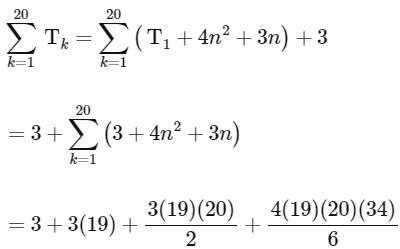
= 3 + 10507
= 10510
Similarly, for (D)
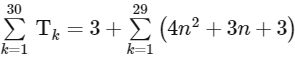
= 35615
Q2: Let l1, l2,…,l100 be consecutive terms of an arithmetic progression with common difference d1, and let w1, w2,…,w100 be consecutive terms of another arithmetic progression with common difference d2, where d1d2 = 10. For each i =1, 2,…,100, let Ri be a rectangle with length li, width wi and area Ai. If A51 − A50 = 1000, then the value of A100 − A90 is __________. [JEE Advanced 2022 Paper 1]
Ans: 18900
Given,
l1, l2,…,l100 are in A.P with common difference d1.
So from property of A.P we can say,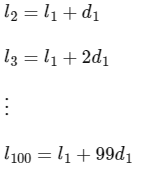
Also given,
w1, w2,…,w100 are in A.P with common difference d2.
∴ From the property of A.P we can say,
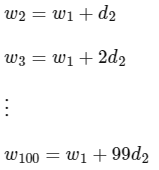
Now, also given,
d1d2 = 10
and Ri is a rectangle whose length is li and width is wi and area Ai.
We know, area of rectangle
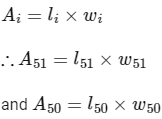
Given,
A51 − A50 = 1000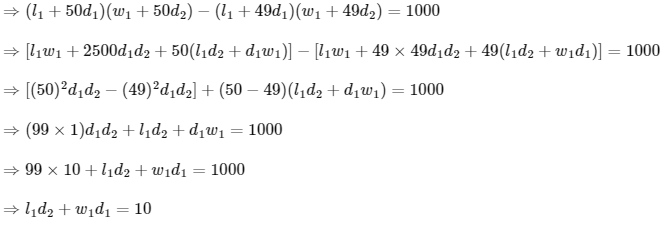
Now,
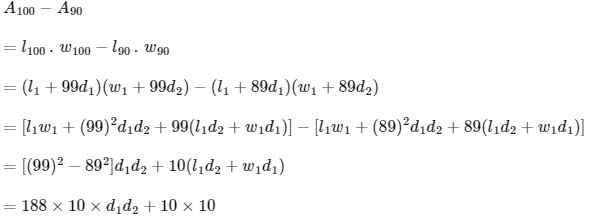
= 1800 x 10 x 10 + 100
= 18800 + 100
= 18900
2020
Q1: Let m be the minimum possible value of 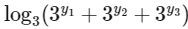 , where y1, y2, y3 are real numbers for which y1+ y2 + y3 = 9. Let M be the maximum possible value of
, where y1, y2, y3 are real numbers for which y1+ y2 + y3 = 9. Let M be the maximum possible value of 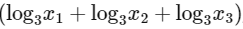 , where x1 , x2, x3 are positive real numbers for which x1 + x2 + x3 = 9. Then the value of
, where x1 , x2, x3 are positive real numbers for which x1 + x2 + x3 = 9. Then the value of  is _________ [JEE Advanced 2020 Paper 1]
is _________ [JEE Advanced 2020 Paper 1]
Ans: 8
For real numbers y1, y2, y3, the quantities 3y1, 3y2 and 3y3 are positive real numbers, so according to the AM-GM inequality, we have
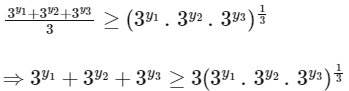
On applying logarithm with base '3', we get
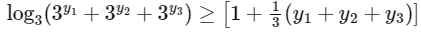
= 1 + 3
= 4
∴ m = 4
Now, for positive real numbers x1, x2 and x3 according to AM-GM inequality, we have
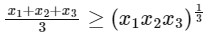
On applying logarithm with base '3', we get
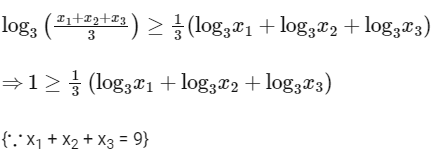
∴ M = 3
Now, 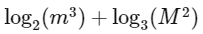
= 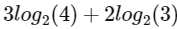
= 6 + 2
= 8
Q2: Let a1, a2, a3, .... be a sequence of positive integers in arithmetic progression with common difference 2. Also, let b1, b2, b3, .... be a sequence of positive integers in geometric progression with common ratio 2. If a1 = b1 = c, then the number of all possible values of c, for which the equality 2(a1 + a2 + ... + an) = b1 + b2 + ... + bn holds for some positive integer n, is ____ [JEE Advanced 2020 Paper 1]
Ans: 1
Given arithmetic progression of positive integers terms a1, a2, a3, ..... having common difference '2' and geometric progression of positive integers terms b1, b2, b3, .... having common ratio '2' with a1 = b1 = c, such that:
2(a1 + a2 + a3 + ... + an) = b1 + b2 + b3 + ... + bn
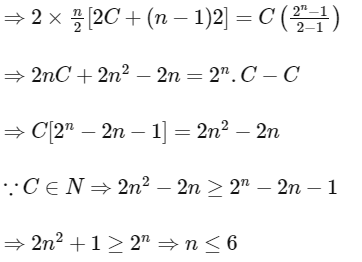
and, also C > 0 ⇒ n > 2
∴ The possible values of n are 3, 4, 5, 6
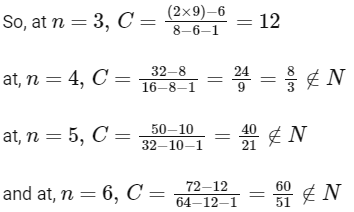
∴ The required value of C = 12 for n = 3
so number of possible value of C is 1
2019
Q1: Let AP(a; d) denote the set of all the terms of an infinite arithmetic progression with first term a and common difference d > 0. If 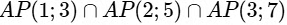 = AP(a ; d), then a + d equals ________ [JEE Advanced 2019 Paper 1]
= AP(a ; d), then a + d equals ________ [JEE Advanced 2019 Paper 1]
Ans: 157
Given that, AP(a ; d) denote the set of all the terms of an infinite arithmetic progression with first term 'a' and common difference d > 0.
Now, let mth term of first progression
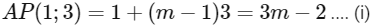
and nth term of progression

and rth term of third progression
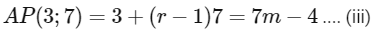 are equal.
are equal.
Then, 3m - 2 = 5n - 3 = 7r - 4
Now, for 
the common terms of first and second progressions, 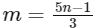
⇒ n = 2, 5, 11, ...
and the common terms of second and the third progressions,
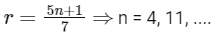
Now, the first common term of first, second and third progressions (when n = 11), so
a = 2 + (11 - 1)5 = 52
and d = LCM (3, 5, 7) = 105
So, 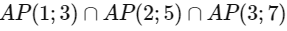 = AP(52; 105)
= AP(52; 105)
So, a = 52 and d = 105
⇒ a + d = 157.00
2018
Q1: Let X be the set consisting of the first 2018 terms of the arithmetic progression 1, 6, 11, ...., and Y be the set consisting of the first 2018 terms of the arithmetic progression 9, 16, 23, .... . Then, the number of elements in the set X ∪ Y is _____. [JEE Advanced 2018 Paper 1]
Ans: 3748
Here, X = {1, 6, 11, ....., 10086}
[∵ an = a + (n − 1)d]
and Y = {9, 16, 23, ..., 14128}
X ∩ Y = {16, 51, 86, ...}
tn of X ∩ Y is less than or equal to 10086
∴ tn = 16 + (n − 1) 35 ≤ 10086
⇒ n ≤ 288.7
∴ n = 288
∵ n(X ∩ Y) = n(X) + n(Y) − n(X ∩ Y)
∴ n(X ∩ Y) = 2018 + 2018 − 288
= 3748
|
209 videos|443 docs|143 tests
|
|
209 videos|443 docs|143 tests
|

|
Explore Courses for JEE exam
|

|

















