JEE Advanced Previous Year Questions (2018 - 2024): Straight Lines | Mathematics (Maths) for JEE Main & Advanced PDF Download
2021
Q1: Consider the lines L1 and L2 defined by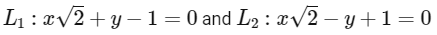
For a fixed constant λ, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is λ2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is √270. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'. ]
The value of λ2 is __________. [JEE Advanced 2021 Paper 1]
Ans: 9
According to the question,
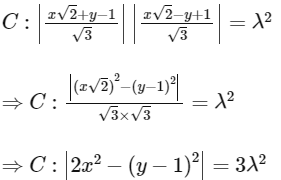
Let R ≡ (x1, y1) and S(x2, y2)
∵ C cuts y − 1 = 2x at R and S.
So, 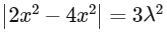
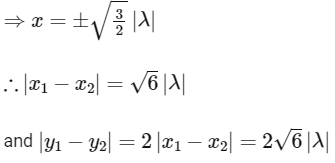
∵ RS2 = 270 (given)
Q2: Consider the lines L1 and L2 defined by
For a fixed constant λ, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is λ2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is √270. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'. ]
The value of D2 is __________. [JEE Advanced 2021 Paper 1]
Ans: 77.14
According to the question,
Let R ≡ (x1, y1) and S(x2, y2)
∵ C cuts y − 1 = 2x at R and S.
So, 
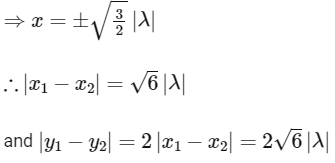
∵ RS2 = 270 (given)
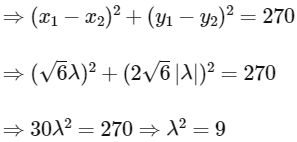
Now, mid-point of RS is 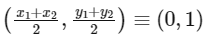 and slope of RS = 2 and slope of
and slope of RS = 2 and slope of 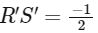
On solving x + 2y − 2 = 0 with C, we get
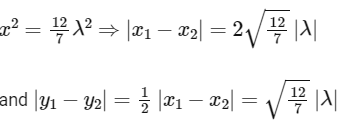
Hence, 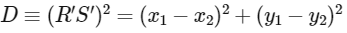
= 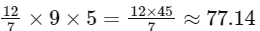
|
172 videos|503 docs|154 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2024): Straight Lines - Mathematics (Maths) for JEE Main & Advanced
| 1. What are some important concepts to understand in straight lines for JEE Advanced? |  |
| 2. How can I find the equation of a line knowing its slope and a point it passes through? |  |
| 3. What is the condition for two lines to be parallel? |  |
| 4. How can I find the distance between a point and a line? |  |
| 5. Can you explain the intercept form of a straight line equation? |  |





















