JEE Exam > JEE Notes > Mathematics (Maths) for JEE Main & Advanced > JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced PDF Download
2023
Q1: Let Q be the cube with the set of vertices {(x1, x2, x3) ∈ R3: x1, x2, x3 ∈ {0, 1}}. Let F be the set of all twelve lines containing the diagonals of the six faces of the cube Q. Let S be the set of all four lines containing the main diagonals of the cube Q; for instance, the line passing through the vertices (0, 0, 0) and (1, 1, 1) is in S. For lines ℓ1 and ℓ2, let d(ℓ1, ℓ2) denote the shortest distance between them. Then the maximum value of d(ℓ1, ℓ2), as ℓ1 varies over F and ℓ2 varies over S, is : [JEE Advanced 2023 Paper 1]
(a) 1√6
(b) 1√8
(c) 1√3
(d) 1√12
Ans: (a)
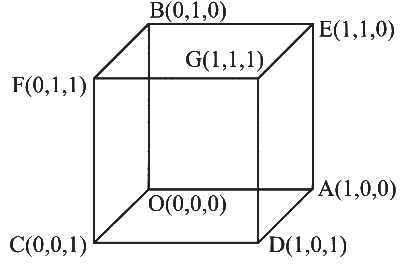
DR'S of OG = 1, 1, 1
DR'S of AF =−1, 1, 1
DR'S of CE = 1, 1, -1
DR'S of BD = 1, -1, 1
Equation OG 
Equation of AB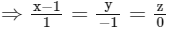 
Normal to both the line's
= 
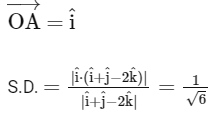
2022
Q1: Let
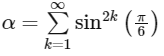Let g : [0, 1] → R be the function defined by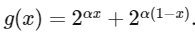 
Then, which of the following statements is/are TRUE ?
(a) The minimum value of g(x) is 27/6
(b) The maximum value of g(x) is 1 + 21/3
(c) The function g(x) attains its maximum at more than one point
(d) The function g(x) attains its minimum at more than one point [JEE Advanced 2022 Paper 2]
Ans: (a), (b) & (c)
Ans: (a), (b) & (c)
Given,
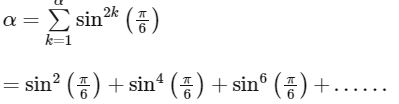
This is a infinite G.P.
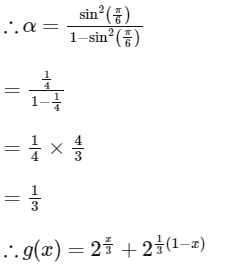
Given x ∈ [0, 1]
We know,
We know, AM = GM when terms are equal.
∴ Option (A) is correct
And option (D) is wrong as at only at a single point x = 1/2, g(x) is minimum.
Now,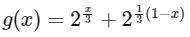 
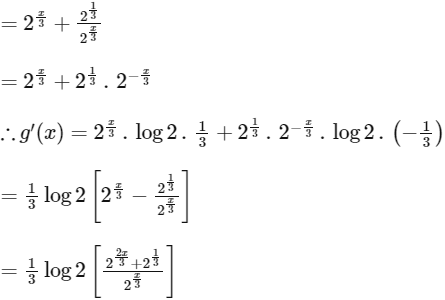
We already found that at x = 1/2 g(x) is minimum.
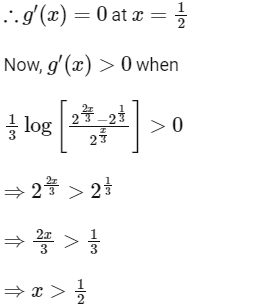
Similarly, g′(x) < 0 when x < 1/2
If we put it in number line we get this
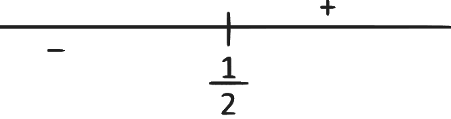
We know g′(x) represent slope of curve g(x) and it is negative when x < 1/2 and positive when x > 1/2 and zero when x = 1/2
∴ Graph of g(x) is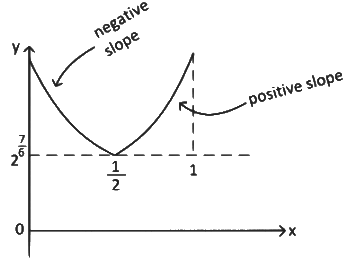
From graph you can see value of g(x) is maximum either at x = 0 or x = 1 in the range x ∈ [0, 1].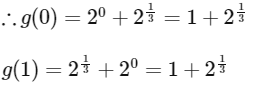 
∴ We get maximum value at x = 0 and x = 1 both.
∴ B and C options are correct.
2020
Q1: Consider the rectangles lying the region
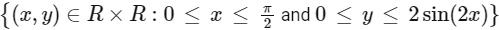
and having one side on the X-axis. The area of the rectangle which has the maximum perimeter among all such rectangles, is
(a) 3π / 2
(b) π
(c)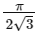 
(d) 
[JEE Advanced 2020 Paper 1]
Ans: (c)
Given region is
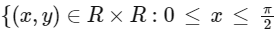and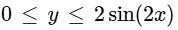 
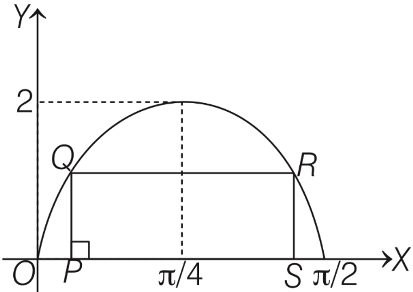
On drawing the diagram,
Let the side PS on the X-axis, such that P(x, 0), and Q(x, 2sin(2x)), so length of the sides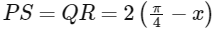 
and PQ = RS = 2sin 2x.
∴ Perimeter of the rectangle
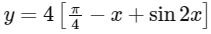
For maximum, dy / dx = 0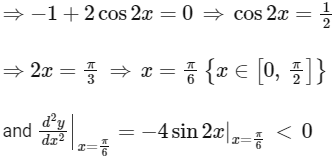
∴ At x = π/6, the rectangle PQRS have maximum perimeter.
So length of sides
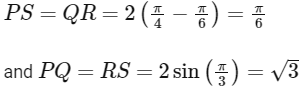
∴ Required area = π/6 x √3 = 
2019
Q1: Let f : R → R be given by f(x) = (x − 1)(x − 2)(x − 5). Define
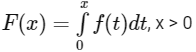
Then which of the following options is/are correct?
(a) F(x) ≠ 0 for all x ∈ (0, 5)
(b) F has a local maximum at x = 2
(c) F has two local maxima and one local minimum in (0, ∞)
(d) F has a local minimum at x = 1 [JEE Advanced 2019 Paper 2]
Ans: (a), (b) & (d)
Given, f : R → and
f(x) = (x − 1)(x − 2)(x − 5)
Since,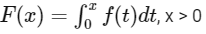 
So,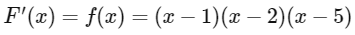 
According to wavy curve method
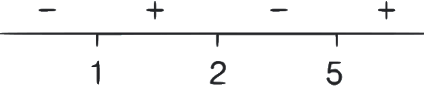
F'(x) changes, it's sign from negative to positive at x = 1 and 5, so F(x) has minima at x = 1 and 5 and as F'(x) changes, it's sign from positive to negative at x = 2, so F(x) has maxima at x = 2.
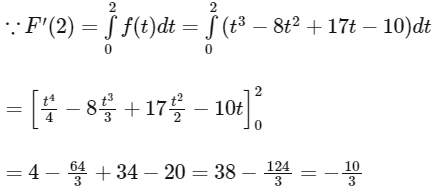
∵ AT the point of maxima x = 2, the functional value F(2), = −10/3, is negative for the interval, x ∈ (0, 5), so F(x) ≠ 0 for any value of x ∈(0, 5),
Hence, options (a), (b) and (d) are correct.
Q2: Let, 
Let x1 < x2 < x3 < ... < xn < ... be all the points of local maximum of f and y1 < y2 < y3 < ... < yn < ... be all the points of local minimum of f.
Then which of the following options is/are correct?
(a) |xn − yn|>1
(b) xn+1 − xn > 2 for every n
(c) x1 < y1
(d)
for every n [JEE Advanced 2019 Paper 2]
Ans: (a), (b) & (d)
Given,
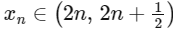for every n [JEE Advanced 2019 Paper 2]Ans: (a), (b) & (d)
Given,
Since, for maxima and minima of f(x), f'(x) = 0
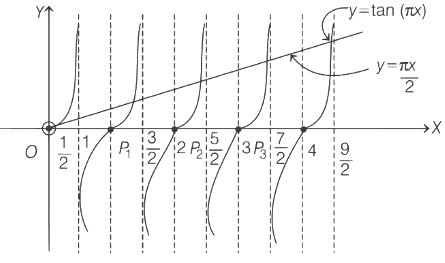
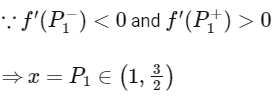
is point of local minimum.
is point of local maximum.
From the graph, for points of maxima x1, x2, x3 .... it is clear that
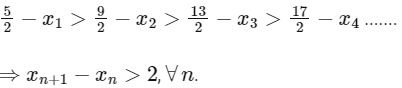
From the graph for points of minima y1, y2, y3 ....., it is clear that
Hence, options (a), (b) and (d) are correct.
2018
Q1: For each positive integer n, let
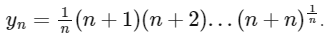
For x ∈ R, let [x] be the greatest integer less than or equal to x. If
, then the value of [L] is _______. [JEE Advanced 2018 Paper 1]Ans: 1
We have,
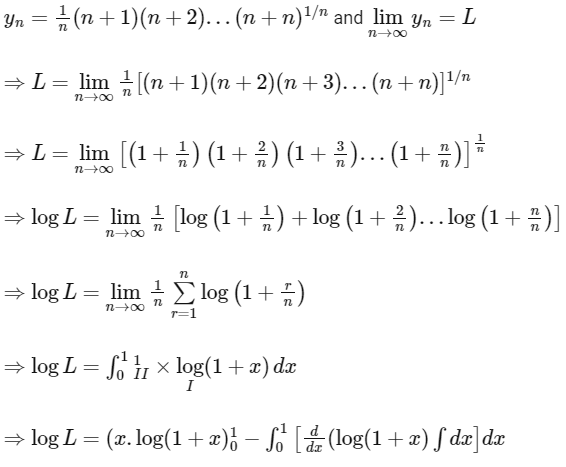
[by using integration by parts]
The document JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced is a part of the JEE Course Mathematics (Maths) for JEE Main & Advanced.
All you need of JEE at this link: JEE
|
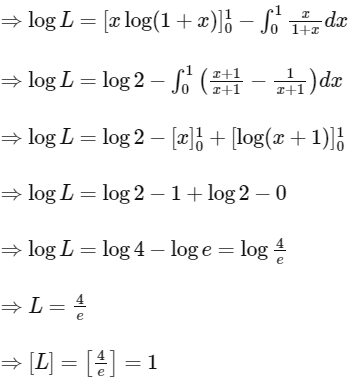
209 videos|443 docs|143 tests
|
FAQs on JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives - Mathematics (Maths) for JEE Main & Advanced
| 1. What is the application of derivatives in JEE Advanced? |  |
Ans. The application of derivatives in JEE Advanced involves using the concept of derivatives to solve various types of problems related to rates of change, optimization, and graph analysis. It helps in finding the maximum and minimum values of functions, determining the rate at which a quantity is changing, and analyzing the behavior of functions using their derivatives.
| 2. How are derivatives applied to find the maximum and minimum values of functions in JEE Advanced? | |
Ans. To find the maximum and minimum values of functions in JEE Advanced, derivatives are used. The critical points of a function, where the derivative is either zero or undefined, are first determined. Then, the first and second derivative tests are applied to these critical points to determine whether they correspond to maximum or minimum values. By analyzing the sign changes of the derivative and the concavity of the function, the maximum and minimum values can be identified.
| 3. Can derivatives be used to determine the rate at which a quantity is changing in JEE Advanced? | |
Ans. Yes, derivatives can be used to determine the rate at which a quantity is changing in JEE Advanced. By finding the derivative of a function representing the quantity with respect to time or another variable, the derivative represents the instantaneous rate of change of the quantity at any given point. This concept is particularly useful in problems involving motion, growth, or decay, where the rate of change is of interest.
| 4. How can derivatives be applied to analyze the behavior of functions in JEE Advanced? | |
Ans. Derivatives can be applied to analyze the behavior of functions in JEE Advanced by examining their increasing and decreasing intervals, as well as their concavity. The sign of the derivative indicates whether the function is increasing or decreasing, while the second derivative determines the concavity. By analyzing the sign changes of the derivative and the concavity, critical points, inflection points, and the overall behavior of the function can be determined.
| 5. What are some common types of problems involving the application of derivatives in JEE Advanced? | |
Ans. Some common types of problems involving the application of derivatives in JEE Advanced include optimization problems, related rates problems, curve sketching problems, and problems involving motion or growth/decay. These problems often require finding maximum or minimum values, determining rates of change, analyzing the behavior of functions, or solving real-life application problems using the concepts of derivatives.
Related Exams
About this Document
|
4.92/5 Rating |
|
Dec 22, 2024 Last updated |
Document Description: JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives for JEE 2024 is part of Mathematics (Maths) for JEE Main & Advanced preparation.
The notes and questions for JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives have been prepared according to the JEE exam syllabus. Information about JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives covers topics
like 2023, 2022, 2020, 2019, 2018 and JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives Example, for JEE 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives.
Introduction of JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives in English is available as part of our Mathematics (Maths) for JEE Main & Advanced
for JEE & JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives in Hindi for Mathematics (Maths) for JEE Main & Advanced course.
Download more important topics related with notes, lectures and mock test series for JEE
Exam by signing up for free. JEE: JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced
Description
Full syllabus notes, lecture & questions for JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced - JEE | Plus excerises question with solution to help you revise complete syllabus for Mathematics (Maths) for JEE Main & Advanced | Best notes, free PDF download
Information about JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives
In this doc you can find the meaning of JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives defined & explained in the simplest way possible. Besides explaining types of
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives theory, EduRev gives you an ample number of questions to practice JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives tests, examples and also practice JEE
tests
|
209 videos|443 docs|143 tests
|
Download as PDF
|
Explore Courses for JEE exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Viva Questions
,ppt
,MCQs
,JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced
,Extra Questions
,Previous Year Questions with Solutions
,JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced
,JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives | Mathematics (Maths) for JEE Main & Advanced
,study material
,practice quizzes
,mock tests for examination
,Exam
,Free
,Sample Paper
,Important questions
,past year papers
,video lectures
,shortcuts and tricks
,Objective type Questions
,Semester Notes
,Summary
,
Additional Information about JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives for JEE Preparation
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives Free PDF Download
The JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives is an invaluable resource that delves deep into the core of the JEE exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives now and kickstart your journey towards success in the JEE exam.
Importance of JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives
The importance of JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives cannot be overstated, especially for JEE aspirants.
This document holds the key to success in the JEE exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives Notes
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives Notes on EduRev are your ultimate resource for success.
JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives JEE
The "JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives JEE Questions" guide is a valuable resource for all aspiring students preparing for the
JEE exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives on the App
Students of JEE can study JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of JEE Advanced Previous Year Questions (2018 - 2023): Application of Derivatives is prepared as per the latest JEE syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup