Dividend decisions and Valuation of Firm | Commerce & Accountancy Optional Notes for UPSC PDF Download
Graham and Dodd Model
Graham and Dodd Model (The traditional position) According to this model the capital markets (investors) are considerably more favorable to companies paying dividends than on companies laying emphasis on retained earnings. This view is expressed quantitatively in the following valuation model advanced by Graham and Dodd.
P = m (D + E/3)
Where,
P = market price per share
D = dividend per share
E = earnings per share
m = multiplier
R = Retained earnings
E = D + R
Replacing E with D+R
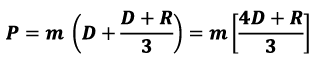
According to this model, dividends contribute four times more to the share price compared to retained earnings.
Dividend Theories-I
- The weights assigned in this model are not based on empirical analysis but on subjective assessment. Nonetheless, the main argument suggests that a generous dividend policy or high payout ratio positively influences stock prices.
- Supporting this argument, it's often mentioned that companies with high payouts tend to have high price-earnings (P/E) ratios, while those with low payouts have low P/E ratios. However, this line of reasoning has significant flaws. Consider a company with a high P/E ratio and a high payout ratio, but current earnings are temporarily depressed. This could lead to two likely scenarios: 1) The dividend payout ratio remains high as companies are reluctant to reduce dividends per share during temporary earnings declines, as investors interpret dividend changes as signals of management's earnings forecast. 2) The price-earnings ratio may stay high during temporary earnings declines because the market looks ahead and discounts future earnings, not just present earnings.
- From these scenarios, one might conclude that a high dividend payout ratio leads to a high price-earnings ratio, but such an inference is flawed.
- Another factor to consider when interpreting payout ratios is the riskiness of a firm's cash flows. Companies with high-risk operations tend to have low payout ratios as management tends to be conservative to prepare for difficult times. Additionally, investors are generally risk-averse and do not pay a premium for risky operations. Therefore, it's flawed to infer that a low payout ratio leads to a low price-earnings ratio, as both low payout ratios and low P/E ratios are the result of risk associated with a firm's operations.
Walter’s Model
Professor James E. Walter, a proponent of this model, argues that dividend policies pursued by firms affect their market price. This model establishes the relationship between the firm’s rate of return (r) and its cost of capital (k) in determining the firm’s dividend policy, which aims to maximize the market price of the firm’s shares. Walter’s assumption is based on the following restrictive assumptions:
- Internal Financing: All investments of the firm are financed through retained earnings, implying that neither debt nor new equity is issued.
- Constant Return and Cost of Capital: The firm maintains a constant rate of return (r) and a constant cost of capital (k) throughout its existence.
- 100 Percent Payout or Retention: The firm either pays out its earnings in full as dividends or retains them entirely for immediate reinvestment.
- Retained Earnings as the Sole Source of Financing: The firm relies solely on retained earnings for financing its operations.
- Constant Earnings Per Share (EPS) and Dividend Per Share: The model assumes that the initial earnings and dividends do not change over time. However, the values of EPS and dividend may be adjusted to illustrate the impact of dividend policy under different profitability scenarios. It is assumed that the values of EPS and dividend remain constant throughout the firm's long and infinite life.
Based on these assumptions, Walter’s Valuation formula is as follows:
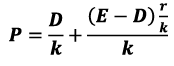 Where,
Where,
P= Market price per share
D = Dividend per share
E = Earnings per share
r = Firm’s rate of return or internal rate of return on firm’s investment
k= Firm’s cost of capital or capitalization rate
An analysis of eq. reveals that the market price per share is the sum of the
- Present value of an infinite stream of constant dividends, and
- Present value of an infinite stream of returns from retained earnings.
Equations is derived as follows: From the explanation given above it is clear that the market price of firm’s share is composed of present value of the infinite stream of dividend D1, D2, D3, Dn, while D1, = D2, = D3,.....= Dn.
The present value of an infinite stream of D is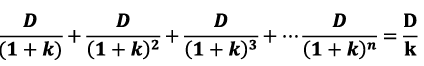
and The present value of an infinite stream of returns from retained earnings - when the firm retains a perpetual sum of (E—D) and invests them at r rate of return its present value is calculated as follows:
Let us assume that every year retained earnings are (E—D) and are reinvested at rate of return r. The return from the first year’s retained earnings would be Note: Retained earnings at time n=l starts earning returns from time = n+l=2. The retained earnings pertaining to time 1 would start earning return from time 2.
Note: Retained earnings at time n=l starts earning returns from time = n+l=2. The retained earnings pertaining to time 1 would start earning return from time 2.
The present value of the return depicted at ‘A’ is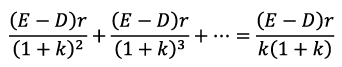
Similarly the return from the second retained earnings would be The present value of the return depicted at ‘B’ is
The present value of the return depicted at ‘B’ is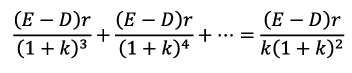 Similarly the present value of the returns from the retained earnings of the third year would be
Similarly the present value of the returns from the retained earnings of the third year would be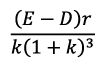 Sum of the present value of the stream of returns from the retained earnings is
Sum of the present value of the stream of returns from the retained earnings is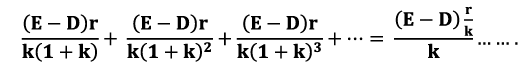
Adding Equation 1 and 2 we get equation 3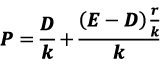
After going through this derivation we can conclude that the value of the share of a firm is a function of the present value of expected future dividends which are constant in this model and the present value of an infinite stream of returns from retained earnings which again remains constant throughout the life of the firm.
Now in order to understand how the optimum dividend policy is dependent on firm’s cost of capital and rate of return let us take an example in which we apply Walter’s model to determine the value of firms share. The variables required to calculate the price are given in the top row of the table.
Dividend Policy and Value o f Firm’s Share (Walter’s Model)

Application of Walter’s Model in Determining Optimal Dividend Payout
The subsequent section elucidates how the Walter’s model is employed to ascertain the optimal dividend payout.
Understanding Growth Firms, Normal Firms, and Declining Firms
- Growth Firms: Growth firms exhibit rates of return surpassing their cost of capital, fostering rapid growth due to abundant investment opportunities yielding returns higher than the cost of capital. Given their need for funds, typically through retained earnings, as per Walter’s model constraints, these firms maximize market price with a 0% payout ratio (retaining all earnings) and minimize it with a 100% payout ratio (distributing all earnings).
- Normal Firms: These firms maintain a rate of return equivalent to their cost of capital. In such cases where r equals k, the dividend policy has no bearing on the market price of the firm's shares. Analysis of Column 2 of Table 14.1 reveals the stability of the payout ratio. For a normal firm, the share price remains unchanged regardless of the dividend policy, indicating the absence of a unique optimal payout ratio.
- Declining firms, on the other hand, experience a rate of return lower than the investors' required minimum rate (Kk). In such cases, investors prefer earnings to be distributed to them so they can invest elsewhere for a higher return than what the declining firm yields. Equity share prices reach their maximum when the firm adopts a maximum payout ratio, as investors are better positioned to earn higher returns than the firm. Thus, the optimal payout ratio for such firms is 100%, meaning zero retained earnings. Share prices increase with higher payout ratios.
According to Walter's model, as shown in Table:
- When the rate of return exceeds the cost of capital (r>k), equity prices rise as the retention ratio decreases. The optimal payout ratio for growth firms is 0%.
- When the rate of return equals the cost of capital (r = k), changes in dividend payout ratio do not affect share prices. The payout ratio for normal firms is inconsequential.
- When the rate of return is less than the cost of capital, share prices increase with higher payout ratios. The optimal payout ratio for declining firms is 100%.
- Interestingly, when the payout ratio is 100%, share prices for the three types of firms do not differ, despite varying returns.
Critical Analysis of Walter's Model:
Walter's model establishes the relationship between dividends, rate of return, and cost of capital for all-equity firms. However, its simplified and restrictive assumptions may lead to conclusions that are not universally applicable. The assumptions of no external financing, constant return, and constant opportunity cost of capital may not hold true in real-world scenarios. Further examination, as illustrated in Figure, reveals how these assumptions deviate in reality.
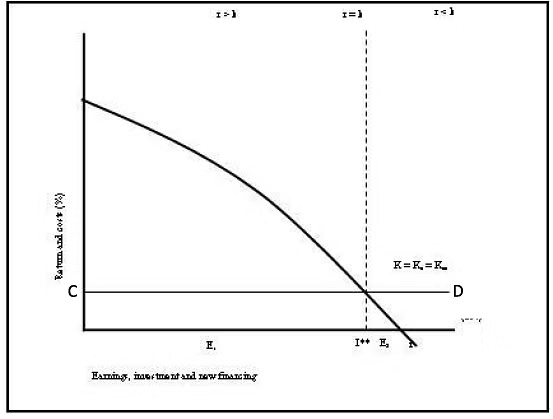
The vertical axis illustrates the rate of return and cost of capital, while the horizontal axis denotes earnings and investments. Curve EF delineates returns across different investment levels. The rate of return (r) on available investment opportunities is presumed to diminish. Line CD represents the constant cost of capital, regardless of the amount of new capital. Now, let's explore how these assumptions diverge:
- No external financing: Walter's model predicates the firm's investment policy on its dividend policy, presuming that new investments are solely funded through retained earnings, without any external financing via debt or equity. In this scenario, the firm's investment policy, or both, may be suboptimal. With diminishing returns on new investments, the most profitable ones are made first, followed by poorer investments. Optimal investment level, Ii, occurs when r equals k. If the firm's earnings, Ei, are less than Ii, external financing (Ii-Ei) is required to reach the optimal investment level. However, Walter's model does not allow access to external financing, resulting in a suboptimal investment policy.
- Constant return (r): Walter's model assumes a constant rate of return (r), whereas in reality, r decreases as investment quantum increases. The firm should halt new investments when r falls below k (cost of capital). If the firm's earnings, E2, exceed Ii (E2>Ii), under the assumption of either 100% payout or 100% retention, the optimal investment of Ii cannot be made. With 100% payout, the surplus of E2-I1 cannot be reinvested, potentially eroding equity holder's wealth if invested at a return lower than k. The optimal policy would involve investing Ii and distributing the surplus of E2-I1 as dividends, but Walter's model does not permit this, thus failing to optimize owner's wealth.
- Constant opportunity cost of capital (k): Walter's model assumes a constant cost of capital (k), whereas in reality, it varies with the firm's risk. The firm's income's present value fluctuates inversely with the cost of capital. By assuming a constant k, Walter's model overlooks the risk element in valuation.
Gordon's Model
Myron Gordon developed a stock valuation model employing the dividend capitalization approach, aiming to correlate the firm's market value with its dividend policy. This model, akin to Walter's model, is built upon specific assumptions:
- All Equity Firm: The firm's capital needs are met solely through equity, without any debt.
- No External Financing: The firm cannot obtain capital from external sources, relying solely on retained earnings for expansion.
- Constant Return: The firm's rate of return remains consistent over its lifespan, disregarding marginal efficiency of investment.
- Constant Cost of Capital: The firm's cost of capital remains steady throughout its existence, disregarding changes in risk classification and subsequent effects on the firm's cost of capital.
- Growth Rate as a Function of Retention Ratio and Rate of Return: The growth rate of the firm is determined by the retention ratio multiplied by the rate of return, stemming from assumptions 2 and 3.
- Constant Retention: Once established, the retention ratio (portion of earnings reinvested) remains constant throughout the firm's lifespan, resulting in perpetual constant growth rate.
- No Taxes: Corporate taxes are absent.
- Perpetual Earnings: The firm and its earnings stream are perpetual.
- Cost of Capital Greater Than Growth Rate: Dividend per share is expected to increase due to retained earnings.
Based on these assumptions, Gordon's fundamental valuation formula is: [Valuation formula to be inserted here].
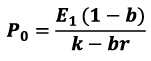 Where,
Where,
- P0= price per share at the beginning of year 0
- E1 = earning per share (EPS) at the end of year
- (1 — b) = fraction of earnings the firm distributes by way of dividends
- b= fraction of earnings the firm ploughs back
- k= rate of return required by the shareholders
- r= rate of return earned by the firm on its investments
- g = br Which is growth rate of earnings and dividends.
The dividend per share in any year is equal to payout ratio (1 — b) times earning per share i.e. Divt = (1 — b)E1 where b is the fraction of earnings of the firm reinvested by the firm at internal rate of return r. Reinvestment of retained earnings allows earnings to grow at g=br per period. Now let us derive the Gordon’s Model which is based on the divooidend capitalization approach. As per the basic valuation model the present value of any asset (share) is the equal to the present value of an infinite stream of cash flows (dividends) expected to be received by the shareholders therefore:
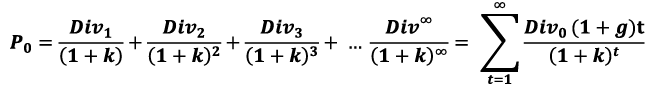 Reinvestment of retained earning where Div0 is dividend at the end of year 0 results in earnings grow per period at the rate of g = br. Incorporating the growth in earnings and dividends as a result of retained earnings in Eq. the present value of a share is determined as
Reinvestment of retained earning where Div0 is dividend at the end of year 0 results in earnings grow per period at the rate of g = br. Incorporating the growth in earnings and dividends as a result of retained earnings in Eq. the present value of a share is determined as
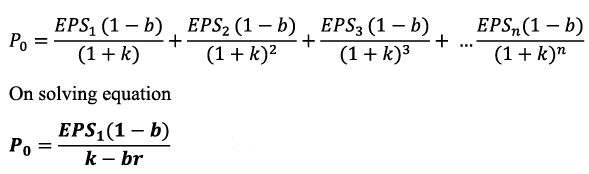
Equation depicts the relationship of expected earnings per share, retained earnings, firm’s rate of return and firms cost of capital. You must be wondering where the variable for dividend in the equation is. Dividend in this equation is depicted by b, which is the retention ratio calculated as (EPS - Dividend)/ EPS, Now let us analyse how the dividend policy as per Gordon’s model effect the share prices of different firms viz., normal firms, growth firms and declining firms.
Now let us again analyse the case of a normal firm wherein the internal rate of return is equal to its cost of capital r = K. Under this condition equation Can be expressed as follows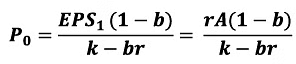
When r = k EPS = rA, Where A is asset of the firm
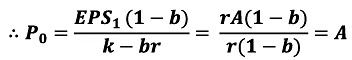
- Eq. clearly shows that when r = fc the firm’s value is not dependent on earnings (EPS) nor on firm’s risk as measured by fc and dividend policy also has no impact on firm’s value. Thus when r = fc the firm’s dividend policy is irrelevant in determining the firm’s value and is solely dependent on the assets it holds. This when analyses in context of competitive conditions implies that the opportunity cost of capital fc of firm shall be equal to the rate of return generally available to share holders if they choose to invest in shares of other similar companies. This further implies that only funds distributed by the company as way of dividend can be invested by shareholders in the shares of other comparable companies earning a rate equal to the firm’s internal rate of return as a result the share holders neither lose nor gain as a consequence of firm’s dividend policy.
- Now let us consider the case of a declining firm where r < fcviz cost of capital is greater than rates of return. By simple intuition we can arrive at conclusion that more the retained earnings the more the value of the company will fall as per eq.
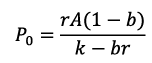
If the retention ratio b is zero viz. payout ratio is 100% eq. becomes
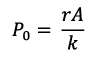
Now if r < k then r < k < 1 which implies that P0 price per share is less than the firm’s investment per share in asset A. Now if the retention ratio is raised the price of the share is going to fall further. These results can be further explained as follows:
- If the rate of return r is less than k the required rate of return by the shareholders; profit retention by the firm would lead to further fall in the price of the share as more and more investors would sell the shares and invest in shares providing r the required rate of return. Increase in retention ratio (less dividend) deprives the share holders to invest at higher rate elsewhere. In such a scenario the better way for the firms would be to follow a policy of contraction and disinvestment which involves not only transfer of net profit but also a part of the paid up capital.
Now, let's examine the scenario of a growth firm where the rate of return, denoted as r, exceeds the cost of capital, denoted as k. In such a case, increasing the retention ratio should lead to an increase in the value of shares. This is because a higher retention ratio results in more capital being available, and this increased capital also earns a rate of return that surpasses the cost of capital. However, within this model, determining the optimal retention ratio is not feasible. For instance, in equation...
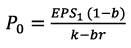
- If b = k / r the denominator k — b r becomes 0 making P0 as negative which is not possible. The reason for these kind of results is the assumptions that r and k are constant which underlies the model. In order to derive meaningful conclusions the value o f b should be less than k / r implying that it should be less than one as in growth firms r would always be greater than k.
- Let us now understand how the Gordon’s model operates under different retention ratios with the help of the following illustration. All the required data is given in the first row of table itself.
Table: Dividend Policy and the Value of firm


An analysis of the table indicates the following:
- For growth firms characterized by r>k, the decision to retain more earnings would result in an increase in the share price of the firm.
- For declining firms characterized by r<k, the decision to retain more earnings would result in a decrease in the share price, while conversely, the decision to distribute the earnings and capital back to shareholders would lead to an increase in the share price of the firm.
- For normal firms characterized by r = k, the decision to retain or distribute the earnings has no bearing on the share price of the firm.
Revised Model: The Bird-In-The-Hand Argument
According to Gordon’s model, dividend policy becomes irrelevant when the rate of return (r) is equivalent to the cost of capital (k), that is, r = k, when all other assumptions are held valid. In order to conform to reality, Gordon modified his basic model to factor in risk and uncertainty. This revision was necessitated by the higher risk and uncertainty associated with future dividends. To incorporate this risk and uncertainty of future dividends, the discount rate applied to dividends increases with time. The revised Gordon’s equation is:
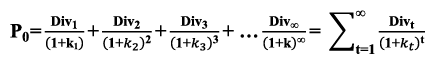
W here Po is the price o f the share w h e n retention ratio is zero.
- In the above equation k1<k2<k3<kt-1<kt.
- If it is assumed that firm retains a fraction of earnings (b), dividend per share will be equal to (1-b) EPS1 in the first year. When the dividend is expected to grow at the rate of g = br, this is contingent upon retained earnings reinvested at r rate of return. The dividend in the second year would be Div0(1+g)2 =(l-b)EPS1(1+br)2 similarly dividend for the third year would be Div0(l+g)3=(l-b)EPS1(1+br)3 and so on for the next years. Discounting these dividends at the corresponding discount rates of k1,k2,k3 kt.1 and kt. We obtain
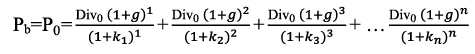
- Pb is the price of share when the retention rate b is positive b>0. Since k1<k2<k3<kt-1<kt. the calculation of this equation becomes little complex. To make calculations simple we discount the dividend stream at an uniform rate of k+, which is the weighted average of all kt s. Replacing k1 k2k3kt-1kt with k+, Pb becomes
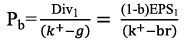
- Now the question which arises is whether Pb is greater or lower than Po.Assuming that the firm’s rate of return r equals the discount rate this model concludes that increase in earnings retention will result in lower share value. This result can be further explained by the assumption of investor’s behavior that assumes that investors are risk averse and they consider future dividends as less certain then near dividends.
- An extension of these assumptions lead us to the conclusion that distant dividends are discounted at higher rates than near dividends; increasing the retention ratio will lead to rising of average discount rate thereby lowering the share price.
|
196 videos|219 docs
|
FAQs on Dividend decisions and Valuation of Firm - Commerce & Accountancy Optional Notes for UPSC
| 1. What is the Graham and Dodd Model and how does it relate to dividend decisions and valuation of a firm? |  |
| 2. How does Walter's Model differ from Gordon's Model in terms of dividend decisions and valuation of a firm? |  |
| 3. What factors should be considered when making dividend decisions according to the models mentioned in the article? |  |
| 4. How can the use of these models help in determining the appropriate dividend policy for a firm? |  |
| 5. In what ways can the concepts of dividend decisions and firm valuation be applied in the context of the UPSC exam or other competitive exams? |  |















