JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics | Physics for JEE Main & Advanced PDF Download
2023
Q1: An ideal gas is in thermodynamic equilibrium. The number of degrees of freedom of a molecule of the gas is n. The internal energy of one mole of the gas is Un and the speed of sound in the gas is vn. At a fixed temperature and pressure, which of the following is the correct option?
(a) v3 < v6 and U3 > U6
(b) v5 > v3 and U3 > U5
(c) v5 > v7 and U5 < U7
(d) v6 < v7 and U6 < U7 [JEE Advanced 2023 Paper 2]
Ans: (c)
1. Formula for Sound Velocity:
- The velocity of sound, denoted as v, is determined by the equation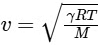 
,
where:-
- γ is a factor given by γ = 1 + 2/n.- R is the gas constant.
- T is the temperature.
- M is the molar mass of the gas.
2. Relation of γ with n:
- The value of γ is inversely related to n. This means as n increases, γ decreases.
3. Internal Energy Relation:
- The internal energy, denoted as U, for a mole of gas is given by U = nRT / 2.
4. Effect of Increasing n on Sound Velocity and Internal Energy:
When the value of n increases:
- The factor γ decreases, according to its formula.
- As a result, the velocity of sound v also decreases, as it is dependent on √γ.
- Conversely, the internal energy Un increases with the increase in n, as evident from the internal energy formula. Therefore, in summary, a higher value of n leads to a lower velocity of sound and higher internal energy in the context of these formulas.
Q2: One mole of an ideal gas expands adiabatically from an initial state (TA, V0) to final state (Tf, 5V0). Another mole of the same gas expands isothermally from a different initial state (TB, V0) to the same final state (Tf, 5V0). The ratio of the specific heats at constant pressure and constant volume of this ideal gas is γ. What is the ratio TA/TB ?
(a) 5γ−1
(b) 51−γ
(c) 5γ
(d) 5γ+1 [JEE Advanced 2023 Paper 1]
Ans: (a)
The expansion of an ideal gas can be analyzed using the thermodynamic relations for adiabatic and isothermal processes.
Adiabatic Expansion: For an adiabatic process, we use the relation involving temperatures and volumes at the initial and final states, which is given by :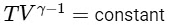
Therefore, for the adiabatic expansion from (TA, V0) to (Tf, 5V0), we have:
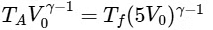
Simplifying, we get :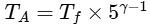 
Isothermal Expansion : In an isothermal process, the temperature remains constant. So, TB = Tf for the isothermal expansion from (TB, V0) to (Tf, 5V0).
To find the ratio TA/TB, we substitute the expressions for TA and TB :
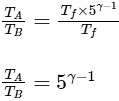
Therefore, the ratio TA/TB is 5γ−1, which corresponds to Option A.
Q3: Match the temperature of a black body given in List-I with an appropriate statement in List-II, and choose the correct option.
[Given: Wien's constant as 2.9 x 10-3 m - K and hc/e = 1.24 x 10-6V - m]
(a) P→3,Q→5,R→2,S→3
(b) P→3,Q→2,R→4,S→1
(c) P→3,Q→4,R→2,S→1
(d) P→1,Q→2,R→5,S→3 [JEE Advanced 2023 Paper 1]
Ans: (c)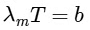
For option (P) temperature is minimum hence λm will be maximum.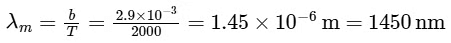 
2θ = width of central maximum
⇒ width ∝ λ
⇒ maximum width of (P)
P → 3
⇒ For option (Q), T = 3000
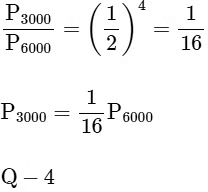
⇒ For (R), T = 5000 K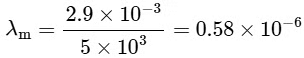
= 580 nmVisible to human eyes
R → 2
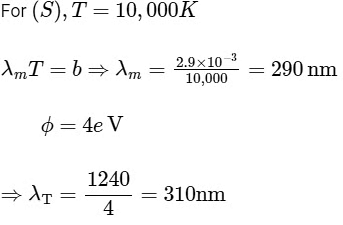
To emit photoelectron
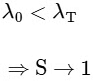
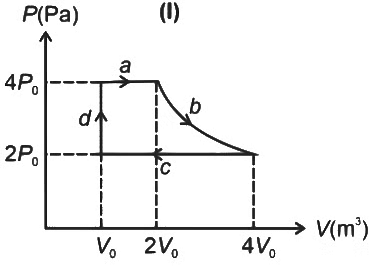
Q4: One mole of an ideal gas undergoes two different cyclic processes I and II, as shown in the P − V diagrams below. In cycle I, processes a, b, c and d are isobaric, isothermal, isobaric and isochoric, respectively. In cycle II, processes a′, b′, c′ and d′ are isothermal, isochoric, isobaric and isochoric, respectively. The total work done during cycle I is WI and that during cycle II is WII. The ratio WI/WII is ________. [JEE Advanced 2023 Paper 2]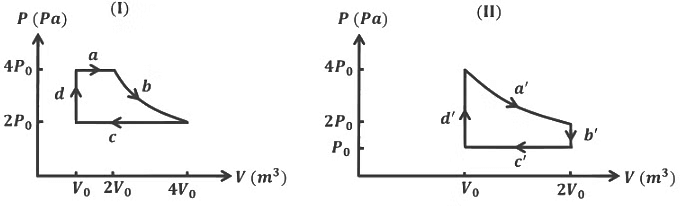
Ans: 2
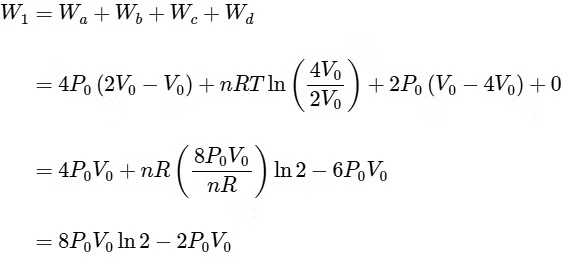
Q5: A cylindrical furnace has height (H) and diameter (D) both 1 m. It is maintained at temperature 360 K. The air gets heated inside the furnace at constant pressure Pa and its temperature becomes T = 360 K. The hot air with density ρ rises up a vertical chimney of diameter d = 0.1 m and height ℎ = 9 m above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density ρa= 1.2 kg m−3, pressure Pa and temperature Ta = 300 K enters the furnace. Assume air as an ideal gas, neglect the variations in ρ and T inside the chimney and the furnace. Also ignore the viscous effects.
[Given: The acceleration due to gravity g = 10 m s−2 and π = 3.14 ] [JEE Advanced 2023 Paper 2]
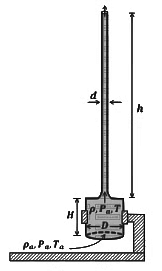
Considering the air flow to be streamline, the steady mass flow rate of air exiting the chimney is _________ gms−1.
Ans: 47.1
We know, 
For a gas R and M are constant. So, ρT = Constant (for constant pressure).
The density of hot air inside the furnace is = ρ
The air gets heated inside the furnace at constant pressure Pa.
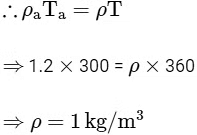
Buoyant force applied on the hot air = ρaVg (Upward direction)
Weight of the hot air = ρaVg (Downward direction)
∴ Net force on the hot air =ρaVg - pVg
Let acceleration of the hot air in the upward direction = a
and mass of the hot air = ρV
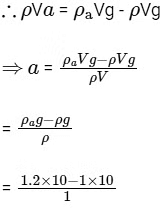
= 2 m/s2
∴ Velocity(v) of the hot air when exiting the chimney using formula v2 = u2 + 2ah
v2 = 0 + 2 x 2 x 9
⇒ v = 6 m/s
Mass flow rate = dm / dt = ρAv
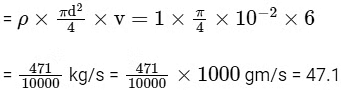
Q6: A cylindrical furnace has height (H) and diameter (D) both 1 m. It is maintained at temperature 360 K. The air gets heated inside the furnace at constant pressure Pa and its temperature becomes T = 360 K. The hot air with density ρ rises up a vertical chimney of diameter d = 0.1 m and height ℎ = 9 m above the furnace and exits the chimney (see the figure). As a result, atmospheric air of density ρa= 1.2 kg m−3, pressure Pa and temperature Ta = 300 K enters the furnace. Assume air as an ideal gas, neglect the variations in ρ and T inside the chimney and the furnace. Also ignore the viscous effects.
[Given: The acceleration due to gravity g = 10 m s−2 and π = 3.14 ] [JEE Advanced 2023 Paper 2]
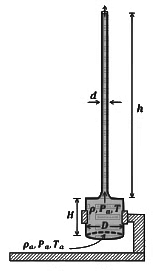
When the chimney is closed using a cap at the top, a pressure difference ΔP develops between the top and the bottom surfaces of the cap. If the changes in the temperature and density of the hot air, due to the stoppage of air flow, are negligible then the value of ΔP is _________ Nm−2.
Ans: 30
We know, 
For a gas R and M are constant. So, ρT = Constant (for constant pressure).
The density of hot air inside the furnace is = ρ
The air gets heated inside the furnace at constant pressure Pa.
After chimney is closed,
Pressure at the bottom surface, P1 = Pa - ρgh = Pa - (1)(10)(9)
Pressure at the bottom surface, P2 = Pa - ρag(h + H) = Pa - (1.2)(10)(9 + 1)
∴ Pressure difference ΔP develops between the top and the bottom surfaces of the cap
= P1 - P2
= Pa - (1)(10)(9) - Pa + (1.2)(10)(9 + 1)
= 120 - 90 = 30
Q7: A closed container contains a homogeneous mixture of two moles of an ideal monatomic gas (γ = 5/3) and one mole of an ideal diatomic gas (γ = 7/5). Here, γ is the ratio of the specific heats at constant pressure and constant volume of an ideal gas. The gas mixture does a work of 66 Joule when heated at constant pressure. The change in its internal energy is _______ Joule. [JEE Advanced 2023 Paper 1]
Ans: 121
First, we identify the heat capacities at constant volume for monatomic and diatomic gases.
For a monatomic ideal gas, the heat capacity at constant volume, Cv1, is (3/2)R. This comes from the degrees of freedom for a monatomic gas, which are three (x, y, and z motions).
For a diatomic ideal gas, the heat capacity at constant volume, Cv2, is (5/2)R. This comes from the degrees of freedom for a diatomic gas, which are five (x, y, and z motions and rotation about two axes).
Next, we find the average heat capacity at constant volume for the gas mixture, Cvmix, which is a weighted average based on the number of moles of each gas :
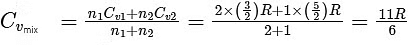
The change in internal energy ΔU for a given number of moles n and change in temperature ΔT is given by :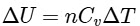
Given that the work done by the system at constant pressure is :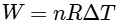
We can replace 
in the equation for ΔU to get :
= 121 Joule
So the change in internal energy is indeed 121 Joule.
2022
Q1: List I describes thermodynamic processes in four different systems. List II gives the magnitudes (either exactly or as a close approximation) of possible changes in the internal energy of the system due to the process.
Which one of the following options is correct?
(a) I → T, II → R, III → S, IV → Q
(b) I → S, II → P, III → T, IV → P
(c) I → P, II → R, III → T, IV → Q
(d) I → Q, II → R, III → S, IV → T [JEE Advanced 2022 Paper 1]
Ans: (c)
= 2.25 kJ − 0.1 k
= 2.15 k
I → P
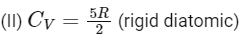
For isobaric expansion
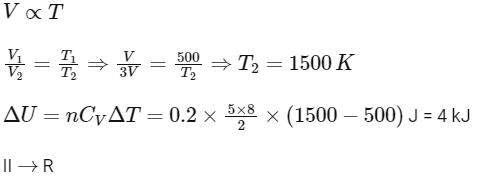
(III) Adiabatic expansion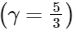 
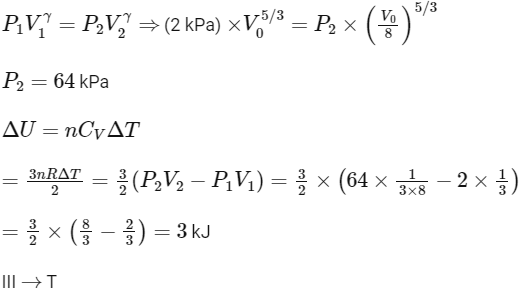
(IV) For isobaric expansion,
[Given: (1/3)0.6 ≃ 0.5, ln2≃0.7 ].
Which of the following statement(s) is(are) correct?
(a) The magnitude of the total work done in the process A→B→C is 144 kJ.
(b) The magnitude of the work done in the process B→C is 84 kJ.
(c) The magnitude of the work done in the process A→B is 60 kJ.
(d) The magnitude of the work done in the process C→A is zero. [JEE Advanced 2022 Paper 2]
Ans: (b), (c) & (d)
For adiabatic process (A→B)
Work done in process A→B
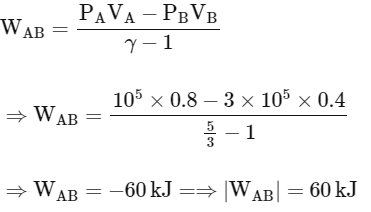
Work done in process B→C (Isothermal process)
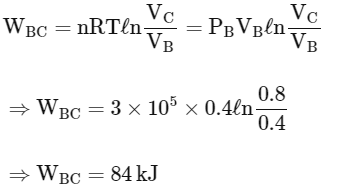
Work done in process C→A
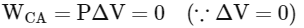
So total work done in the process A→B→C
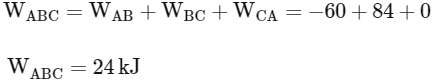
So correct options are (B,C,D)
2021
Q1: A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, CV = 2R. Here, R is the gas constant. Initially, each side has a volume V0 and temperature T0. The left side has an electric heater, which is turned on at very low power to transfer heat Q to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to V0/2. Consequently, the gas temperatures on the left and the right sides become TL and TR, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.
The value of TR / T0 is
(a) √2
(b) √3
(c) 2
(d) 3 [JEE Advanced 2021 Paper 2]
Ans: (a)
Q2: A thermally insulating cylinder has a thermally insulating and frictionless movable partition in the middle, as shown in the figure below. On each side of the partition, there is one mole of an ideal gas, with specific heat at constant volume, CV = 2R. Here, R is the gas constant. Initially, each side has a volume V0 and temperature T0. The left side has an electric heater, which is turned on at very low power to transfer heat Q to the gas on the left side. As a result the partition moves slowly towards the right reducing the right side volume to V0/2. Consequently, the gas temperatures on the left and the right sides become TL and TR, respectively. Ignore the changes in the temperatures of the cylinder, heater and the partition.
The value of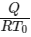 
is
(a) 
(b)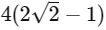 
(c)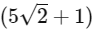 
(d)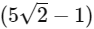 
[JEE Advanced 2021 Paper 2]
Ans: (b)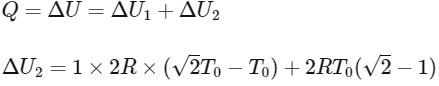
For ΔU2 : Using mole conservation of left side.
Q3: An ideal gas undergoes a four step cycle as shown in the P-V diagram below. During this cycle, heat is absorbed by the gas in
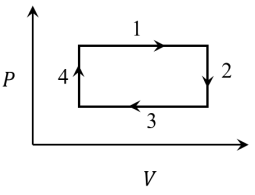(a) steps 1 and 2
(b) steps 1 and 3
(c) steps 1 and 4
(d) steps 2 and 4 [JEE Advanced 2021 Paper 1]
Ans: (c)
Process 1
p = constant, Volume increases and temperature also increases
Q = W + ΔU
∴ W = positive, ΔU = positive
⇒ Heat is positive and supplied to the gas.
Process 2
V = constant, Pressure decreases
T ∝ pV [as V = constant]
⇒ Temperature decreases
W = 0
ΔT is negative and ΔU = f / 2nRΔT
∴ ΔU is also negative
Q = ΔU + W
∴ Heat is negative and rejected by gas.
Process
p = constant, Volume decreases
⇒ Temperature also decreases
W = pΔV = negative
ΔU = f/2nRΔT = negative
∴ Heat is negative and rejected by gas
Process 4
V = constant, Pressure increases
W = 0 (as V = constant)
pV = nRT ⇒ Temperature increase
⇒ ΔU = f/2nRΔT is positive
ΔQ = ΔU + W = positive
Q4: A soft plastic bottle, filled with water of density 1 gm/cc, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of 5 gm, and it is made of a thick glass of density 2.5 gm/cc. Initially the bottle is sealed at atmosphere pressure p0 = 105 Pa so that the volume of the trapped air is v0 = 3.3 cc. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure p0 + Δp without changing its orientation. At this pressure, the volume of the trapped air is v0 − Δv. Let Δv = X cc and Δp = Y × 103 Pa.
The value of X is _______________. [JEE Advanced 2021 Paper 2]
Ans: 0.3
When the tube just sinks/floats, then average density = density of water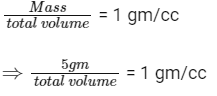
⇒ Total volume = 5 cc
⇒ Volume of tube + final volume of air in the tube = 5 cc
⇒ Vf = 5 − 2 = 3 cc
⇒ ΔV = 0.3 cc
Q5: A soft plastic bottle, filled with water of density 1 gm/cc, carries an inverted glass test-tube with some air (ideal gas) trapped as shown in the figure. The test-tube has a mass of 5 gm, and it is made of a thick glass of density 2.5 gm/cc. Initially the bottle is sealed at atmosphere pressure p0 = 105 Pa so that the volume of the trapped air is v0 = 3.3 cc. When the bottle is squeezed from outside at constant temperature, the pressure inside rises and the volume of the trapped air reduces. It is found that the test tube begins to sink at pressure p0 + Δp without changing its orientation. At this pressure, the volume of the trapped air is v0 − Δv. Let Δv = X cc and Δp = Y × 103 Pa.
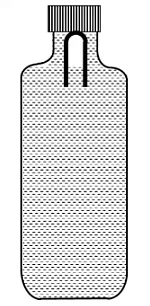The value of Y is _______________. [JEE Advanced 2021 Paper 2]
Ans: 0.3
When the tube just sinks/floats, then average density = density of water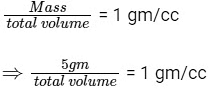
⇒ Total volume = 5 cc
⇒ Volume of tube + final volume of air in the tube = 5 cc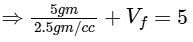
⇒ Vf = 5 − 2 = 3 cc
⇒ ΔV = 0.3 cc
For isothermal process,
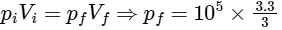
pf = 1.1 × 105
pf − pi = 1.1 × 105 − 105
= 0.1 × 105 = 10 × 103 Pa
⇒ Y = 10
Q6: A small object is placed at the center of a large evacuated hollow spherical container. Assume that the container is maintained at 0 K. At time t = 0, the temperature of the object is 200 K. The temperature of the object becomes 100 K at t = t1 and 50 K at t = t2. Assume the object and the container to be ideal black bodies. The heat capacity of the object does not depend on temperature. The ratio (t2/t1) is ____________. [JEE Advanced 2021 Paper 1]
Ans: 9
Ts = 0 K
Ti = 200 K, e = 1
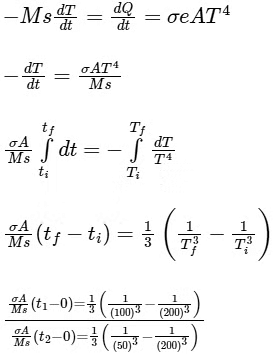
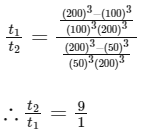
2020
Q1: The filament of a light bulb has surface area 64 mm2 . The filament can be considered as a black body at temperature 2500 K emitting radiation like a point source when viewed from far. At night the light bulb is observed from a distance of 100 m. Assume the pupil of the eyes of the observer to be circular with radius 3 mm. Then [JEE Advanced 2020 Paper 1 ]
(Take Stefan-Boltzmann constant = 5.67 × 10−8 Wm−2K−4 , Wien’s displacement constant = 2.90 × 10−3 m-K, Planck’s constant = 6.63 × 10−34 Js, speed of light in vacuum = 3.00 × 108 ms−1)
(a) power radiated by the filament is in the range 642 W to 645 W
(b) radiated power entering into one eye of the observer is in the range 3.15 × 10−8 W to 3.25 × 10−8 W
(c) the wavelength corresponding to the maximum intensity of light is 1160 nm
(d) taking the average wavelength of emitted radiation to be 1740 nm, the total number of photons entering per second into one eye of the observer is in the range 2.75 × 1011 to 2.85 × 1011
Ans: (b), (c) & (d)
Here, A = 64 mm2, T = 2500K (where, A = surface area of filament, T = temperature of filament, d is distance of bulb from observer and Re = radius of pupil of eye)
Point source, d = 100 m, Re = 3 mm
(a) P = σAeT−4
= 5.67 × 10−8 × 64 × 10−6 × 1 × (2500)4
(∵ e = 1 for black body)
= 141.75 W
(b) Power reaching to the eye
(c)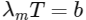
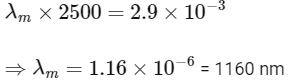
(d) Power received by one eye of observer =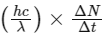 
where, ΔN / Δt = number of photons.
entering into eye per second.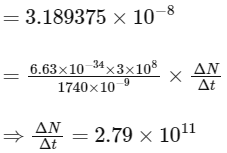
Q2: A container with 1 kg of water in it is kept in sunlight, which causes the water to get warmer than the surroundings. The average energy per unit time per unit area received due to the sunlight is 700 Wm−2 and it is absorbed by the water over an effective area of 0.05m2. Assuming that the heat loss from the water to the surroundings is governed by Newton's law of cooling, the difference (in ∘C) in the temperature of water and the surroundings after a long time will be ___________. (Ignore effect of the container, and take constant for Newton's law of cooling = 0.001 s−1, Heat capacity of water = 4200 J kg−1 K−1) [JEE Advanced 2020 Paper 2]
Ans: 8.33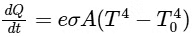
For small temperature change,
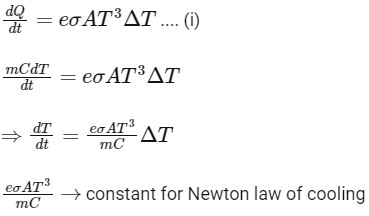
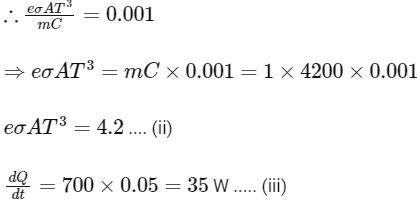
Putting the value of Eqs. (ii) and (iii) in Eq. (i), we get
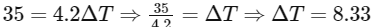
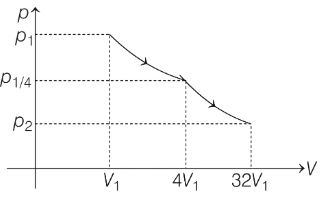
Q3: Consider one mole of helium gas enclosed in a container at initial pressure P1 and volume V1. It expands isothermally to volume 4V1. After this, the gas expands adiabatically and its volume becomes 32V1. The work done by the gas during isothermal and adiabatic expansion processes are Wiso and Wadia, respectively. If the ratio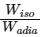 
= f ln 2, then f is ______. [JEE Advanced 2020 Paper 1]
Ans: 1.77
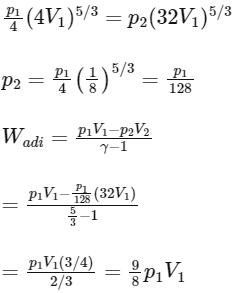
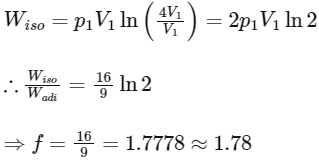
2019
Q1: In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by TΔX where T is temperature of the system and ΔX is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas, 
Here, R is gas constant, V is volume of gas, TA and VA are constants.
The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.
If the process on one mole of monatomic ideal gas is as shown in the TV-diagram with P0V0 = 1/3RT0, the correct match is,
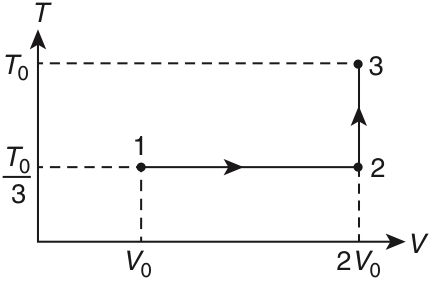
(a) I → P, II → R, III → T, IV → S
(b) I → P, II → T, III →Q, IV → T
(c) I → S, II → T, III → Q, IV → U
(d) I → P, II → R, III → T, IV → P [JEE Advanced 2019 Paper 2]
Ans: (d)
1-2 process is isothermal and 2-3 process is isochoric.
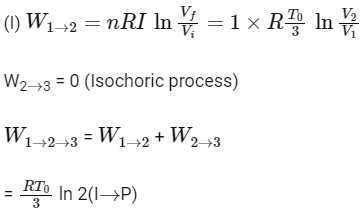
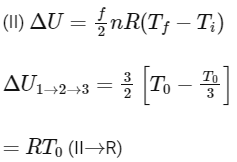
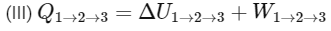(First law of thermodynamics)
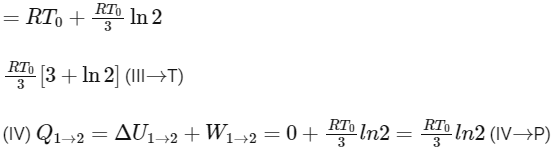
Q2: A mixture of ideal gas containing 5 moles of monatomic gas and 1 mole of rigid diatomic gas is initially at pressure P0, volume V0, and temperature T0. If the gas mixture is adiabatically compressed to a volume V0 / 4, then the correct statement(s) is/are
(Given, 21.2 = 2.3; 23.2 = 9.2; R is a gas constant)
(a) The final pressure of the gas mixture after compression is in between 9P0 and 10P0
(b) The average kinetic energy of the gas mixture after compression is in between 18RT0 and 19RT0
(c) Adiabatic constant of the gas mixture is 1.6
(d) The work |W| done during the process is 13RT0 [JEE Advanced 2019 Paper 2]
Ans: (a), (c) & (d)
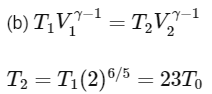
Average kinetic energy of gas mixture
= 
2018
Q1: One mole of a monatomic ideal gas undergoes four thermodynamic processes as shown schematically in the PV-diagram below. Among these four processes, one is isobaric, one is isochoric, one is isothermal and one is adiabatic.
Match the processes mentioned in List-I with the corresponding statements in List-II.
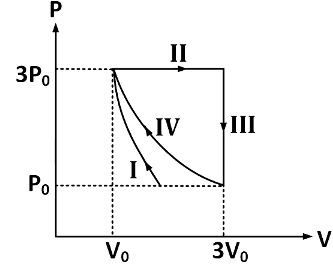
Ans: (c)
Process I is adiabatic, therefore,
⇒ ΔQ = ΔU + W ⇒ W = −Δ
Thus, W < 0 since volume of gas is decreasing ⇒ ΔU > 0 Therefore, temperature of gas increases and no heat is exchanged between gas and surroundings
Thus, the correct mapping is P → 3
Process II is isobaric, therefore, pressure remains constant
⇒ W = PΔV = 3P0[3V0 − V0] = 6P0V
Therefore, work done by gas in process II is 6P0V0.
Thus, the correct mapping is Q → 4.
Process III is isochoric, therefore, volume remains constant
⇒ ΔQ = ΔU + W ⇒ ΔQ = ΔU
and work done by gas is zero.
Thus, the correct mapping is R → 1.
Process IV is isothermal process, therefore temperature remains constant
⇒ ΔQ = ΔU + W ⇒ ΔQ = W and Δ = 0
Thus, the correct mapping is S → 2.
Therefore, option (C) is correct.
Q2: One mole of a monatomic ideal gas undergoes a cyclic process as shown in the figure (where V is the volume and T is the temperature). Which of the statements below is (are) true?
(b) In process II, gas absorbs heat
(c) In process IV, gas releases heat
(d) Process I and III are not isobaric [JEE Advanced 2018 Paper 1]
Ans: (b), (c) & (d)
In process I, volume is changing. Therefore, it is not isochoric. Therefore 'A' is incorrect.
In process II, q = ΔU + W . ΔU = 0 as temperature is constant. Therefore, q = W. Here W = P(Vf − Vi) is positive therefore q is positive i.e., gas absorbs heat. Therefore 'B' is correct.
For process IV, q = ΔU + W. Here Δ = 0 and W is negative (volume decreases). Therefore q is negative i.e., gas releases heat. 'C' is correct.
For an isobaric process, V ∝ T i.e., we will get a straight inclined line in T-V graph. Therefore I and II are NOT isobaric. 'D' is correct.
Q3: One mole of a monatomic ideal gas undergoes an adiabatic expansion in which its volume becomes eight times its initial value. If the initial temperature of the gas is 100K and the universal gas constant R = 8.0 J mol−1K−1, the decrease in its internal energy, in Joule, is ____________. [JEE Advanced 2018 Paper 2]
Ans: 900
|
289 videos|635 docs|179 tests
|
|
Nov 23, 2024 Last updated |
|
Explore Courses for JEE exam
|
|
Previous Year Questions with Solutions
,JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics | Physics for JEE Main & Advanced
,Summary
,ppt
,video lectures
,mock tests for examination
,shortcuts and tricks
,Viva Questions
,JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics | Physics for JEE Main & Advanced
,JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics | Physics for JEE Main & Advanced
,Extra Questions
,Objective type Questions
,MCQs
,practice quizzes
,Free
,past year papers
,Important questions
,Sample Paper
,Semester Notes
,study material
,Exam
;
JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics Free PDF Download
Importance of JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics
JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics Notes
JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics JEE
Study JEE Advanced Previous Year Questions (2018 - 2023): Thermodynamics on the App
|
© EduRev
|
Education Revolution
|
Follow Us
|
