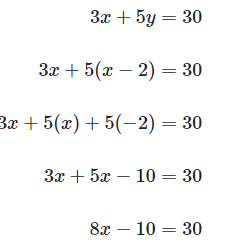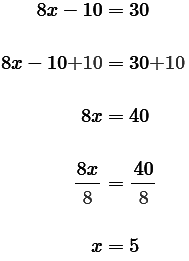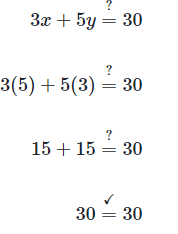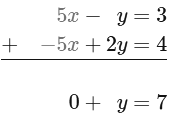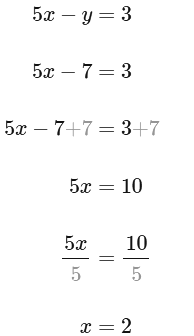Solved Examples: Linear Equations in Two Variables | Mathematics for Digital SAT PDF Download

What are Systems of Linear Equations?
A system of linear equations is usually a set of two linear equations with two variables.
- x + y = 5 and 2x - y = 1 are both linear equations with two variables.
- When considered together, they form a system of linear equations.
A linear equation with two variables has an infinite number of solutions (for example, consider how (0,5),(1,4),(2,3), etc. are all solutions to the equation x + y = 5). However, systems of two linear equations with two variables can have a single solution that satisfies both solutions
- (2,3) is the only solution to both x + y = 5 and 2x - y = 1.
Solved Example
Q1: y = x - 2
3x + 5y = 30
If (x,y) is a solution to the system of equations above, what is the value of x ?
(a) 3
(b) 5
(c) 8
(d) 15
Ans: (b)
Since y is isolated in the first equation, we can use substitution to solve the system of equations.Substituting x- 2 for y in the second equation gives us:We can solve for x:We can verify that 5 is the value of x. Plugging 5 into the first equation for x lets us calculate y :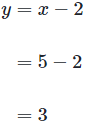 Next, we need to check whether (5, 3) satisfies the second equation:
Next, we need to check whether (5, 3) satisfies the second equation:The value of x is 5
Q2: 5x - y = 3
-5x + 2y = 4
Which ordered pair (x, y) satisfies the given system of equations?
(a) (2/5, -1)
(b) (4/5, 1)
(c) (1, 2)
(d) (2, 7)
Ans: (d)
Since the first equation in the system has the term 5x and the second has the term -5x , we can use elimination to solve the system of equations.
Note: We could also solve the system using substitution, but in this instance the two equations contain terms that can be readily eliminated.
Since 5cx and -5x are opposites, we can add the two equations to eliminate the x -terms.
7 is the value of y
We can plug 7 into the first equation for y and solve for x :
(2, 7) satisfies the system of equations shown above.
Q3: Find the value of variables which satisfies the following equation:
2x + 5y = 20 and 3x+6y =12.
Ans:
Using the method of substitution to solve the pair of linear equation, we have:
2x + 5y = 20 …….(i)
3x+6y =12 ……..(ii)
Multiplying equation (i) by 3 and (ii) by 2, we have:
6x + 15y = 60 …….(iii)
6x+12y = 24 ……..(iv)
Subtracting equation (iv) from (iii)
3y = 36
⇒ y = 12
Substituting the value of y in any of the equation (i) or (ii), we have
2x + 5(12) = 20
⇒ x = −20
Therefore, x=-20 and y =12 is the point where the given equations intersect.
Q4: A boat running downstream covers a distance of 20 km in 2 hours while for covering the same distance upstream takes 5 hours. What is the speed of the boat in still water?
Ans:
These types of questions are the real-time examples of linear equations in two variables.
In water, the direction along the stream is called downstream. And, the direction against the stream is called upstream.
Let us consider the speed of a boat is u km/h and the speed of the stream is v km/h, then:
Speed Downstream = (u + v) km/h
Speed Upstream = (u – v) km/h
We know that, Speed = Distance/Time
So, the speed of boat when running downstream = (20⁄2) km/h = 10 km/h
The speed of boat when running upstream = (20⁄5) km/h = 4 km/h
From above, u + v = 10…….(1)
u – v = 4 ………. (2)
Adding equation 1 and 2, we get: 2u = 14
u = 7 km/h
Also, v = 3 km/h
Therefore, the speed of the boat in still water = u = 7 km/h
Q5: Solve the following system of equations using the substitution method.
x + 2y - 7=0
2x - 5y + 13 = 0
Ans:
Let us solve the equation, x + 2y - 7 = 0 for y:
x + 2y - 7 = 0
⇒ 2y = 7 - x
⇒ y = (7 - x)/2Substitute this in the equation, 2x - 5y + 13 = 0:
2x - 5y + 13=0
⇒ 2x - 5((7 - x)/2) + 13=0
⇒ 2x - (35/2) + (5x/2) + 13 = 0
⇒ 2x + (5x/2) = 35/2 - 13
⇒ 9x/2 = 9/2
⇒ x = 1Substitute x=1 this in the equation y=(7 - x)/2:
y = (7 - 1)/2 = 3
Therefore, the solution of the given system is x = 1 and y = 3.
Q6: Solve the following system of equations using the elimination method.
2x + 3y - 11 = 0
3x + 2y - 9 = 0
Ans:
Adding or subtracting these two equations would not result in the cancellation of any variable. Let us aim at the cancellation of x. The coefficients of x in both equations are 2 and 3. Their LCM is 6. We will make the coefficients of x in both equations 6 and -6 such that the x terms get canceled when we add the equations.
3 × (2x + 3y - 11 = 0)
⇒ 6x + 9y - 33 = 0
-2 × (3x + 2y - 9 = 0)
⇒ -6x - 4y + 18 = 0Now we will add these two equations:
6x + 9y - 33 = 0
-6x - 4y + 18 = 0On adding both the above equations we get,
⇒ 5y - 15 = 0
⇒ 5y = 15
⇒ y = 3Substitute this in one of the given two equations and solve the resultant variable for x.
2x + 3y - 11 = 0
⇒ 2x + 3(3) - 11 = 0
⇒ 2x + 9 - 11= 0
⇒ 2x = 2
⇒ x = 1Therefore, the solution of the given system of equations is x = 1 and y = 3.
|
184 videos|124 docs|75 tests
|
FAQs on Solved Examples: Linear Equations in Two Variables - Mathematics for Digital SAT
| 1. What are systems of linear equations? |  |
| 2. How are systems of linear equations solved? |  |
| 3. What is the importance of systems of linear equations? |  |
| 4. Can systems of linear equations have no solution or infinite solutions? |  |
| 5. How can systems of linear equations be represented geometrically? |  |