Understanding the Law | Physics for EmSAT Achieve PDF Download
Newton’s Second Law for Rotation
We have thus far found many counterparts to the translational terms used throughout this text, most recently, torque, the rotational analog to force. This raises the question: Is there an analogous equation to Newton’s second law, 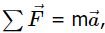 which involves torque and rotational motion? To investigate this, we start with Newton’s second law for a single particle rotating around an axis and executing circular motion. Let’s exert a force
which involves torque and rotational motion? To investigate this, we start with Newton’s second law for a single particle rotating around an axis and executing circular motion. Let’s exert a force 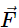 on a point mass m that is at a distance r from a pivot point (Figure). The particle is constrained to move in a circular path with fixed radius and the force is tangent to the circle. We apply Newton’s second law to determine the magnitude of the acceleration a = F/m in the direction of
on a point mass m that is at a distance r from a pivot point (Figure). The particle is constrained to move in a circular path with fixed radius and the force is tangent to the circle. We apply Newton’s second law to determine the magnitude of the acceleration a = F/m in the direction of 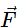 . Recall that the magnitude of the tangential acceleration is proportional to the magnitude of the angular acceleration by a = rα. Substituting this expression into Newton’s second law, we obtain
. Recall that the magnitude of the tangential acceleration is proportional to the magnitude of the angular acceleration by a = rα. Substituting this expression into Newton’s second law, we obtain
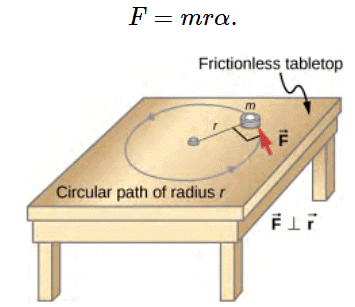
Figure: An object is supported by a horizontal frictionless table and is attached to a pivot point by a cord that supplies centripetal force. A force
is applied to the object perpendicular to the radius r, causing it to accelerate about the pivot point. The force is perpendicular to r.
Multiply both sides of this equation by r,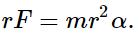
Note that the left side of this equation is the torque about the axis of rotation, where r is the lever arm and F is the force, perpendicular to r. Recall that the moment of inertia for a point particle is I = mr2. The torque applied perpendicularly to the point mass in Figure is therefore
τ = Iα.
The torque on the particle is equal to the moment of inertia about the rotation axis times the angular acceleration. We can generalize this equation to a rigid body rotating about a fixed axis.
The term Iα is a scalar quantity and can be positive or negative (counterclockwise or clockwise) depending upon the sign of the net torque. Remember the convention that counterclockwise angular acceleration is positive. Thus, if a rigid body is rotating clockwise and experiences a positive torque (counterclockwise), the angular acceleration is positive.
Newton’s second law for rotation and tells us how to relate torque, moment of inertia, and rotational kinematics. This is called the equation for rotational dynamics. With this equation, we can solve a whole class of problems involving force and rotation. It makes sense that the relationship for how much force it takes to rotate a body would include the moment of inertia, since that is the quantity that tells us how easy or hard it is to change the rotational motion of an object.
Deriving Newton’s Second Law for Rotation in Vector Form
As before, when we found the angular acceleration, we may also find the torque vector. The second law 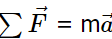 tells us the relationship between net force and how to change the translational motion of an object. We have a vector rotational equivalent of this equation, which can be found by using Equation and Figure Equation relates the angular acceleration to the position and tangential acceleration vectors:
tells us the relationship between net force and how to change the translational motion of an object. We have a vector rotational equivalent of this equation, which can be found by using Equation and Figure Equation relates the angular acceleration to the position and tangential acceleration vectors: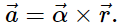
We form the cross product of this equation with 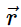 and use a cross product identity (note that
and use a cross product identity (note that 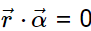 ):
):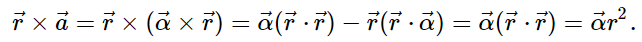
We now form the cross product of Newton’s second law with the position vector 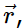
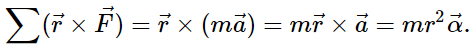
Identifying the first term on the left as the sum of the torques, and mr2 as the moment of inertia, we arrive at Newton’s second law of rotation in vector form: 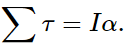
This equation is exactly Equation but with the torque and angular acceleration as vectors. An important point is that the torque vector is in the same direction as the angular acceleration.
Applying the Rotational Dynamics Equation
Before we apply the rotational dynamics equation to some everyday situations, let’s review a general problem-solving strategy for use with this category of problems.
We do not actually need the force of static friction to keep an object rolling on a flat surface (as I mentioned above, the motion could in principle go on “unforced” forever), but things are different on an inclined plane. Figure shows an object rolling down an inclined plane, and the corresponding extended free-body diagram.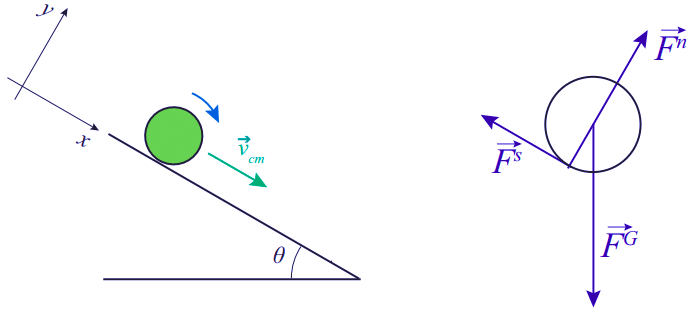
Figure: An object rolling down an inclined plane, and the extended free-body diagram. Note that neither gravity (applied at the CM) nor the normal force (whose line of action passes through the CM) exert a torque around the center of mass; only the force of static friction, 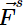 does.
does.
The basic equations we use to solve for the object’s motion are the sum of forces equation: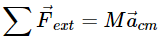
the net torque equation, with torques taken around the center of mass.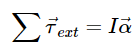
and the extension of the condition of rolling without slipping, to the accelerations: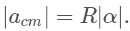
For the situation shown in Figure, if we take down the plane as the positive direction for linear motion, and clockwise torques as negative, we have to write acm = - Rα In the direction perpendicular to the plane, we conclude from that Fn = M g cosθ , an equation we will not actually need; in the direction along the plane, we have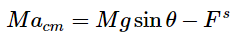
and the torque equation just gives −F s R=Iα , which with acm = −Rα becomes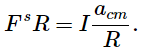
We can eliminate Fs in between these two equations and solve for acm: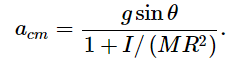
Now you can see why, earlier in the semester, we were always careful to assume that all the objects we sent down inclined planes were sliding, not rolling! The acceleration for a rolling object is never equal to simply gsinθ . Most remarkably, the correction factor depends only on the shape of the rolling object, and not on its mass or size, since the ratio of I to MR2 is independent of m and R for any given geometry. Thus, for instance, for a disk, 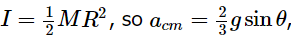 whereas for a hoop,
whereas for a hoop, 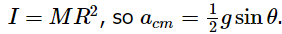 So any disk or solid cylinder will always roll down the incline faster than any hoop or hollow cylinder, regardless of mass or size.
So any disk or solid cylinder will always roll down the incline faster than any hoop or hollow cylinder, regardless of mass or size.
This rather surprising result may be better understood in terms of energy. First, let's show (a result that is somewhat overdue) that for a rigid object that is rotating around an axis passing through its center of mass with angular velocity ω we can write the total kinetic energy as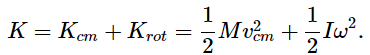
This is because for every particle the velocity can be written as 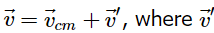 is the velocity relative to the center of mass (that is, in the CM frame). Since in this frame the motion is a simple rotation, we have |v′|=ωr , where r is the particle’s distance to the axis. Therefore, the kinetic energy of that particle will be
is the velocity relative to the center of mass (that is, in the CM frame). Since in this frame the motion is a simple rotation, we have |v′|=ωr , where r is the particle’s distance to the axis. Therefore, the kinetic energy of that particle will be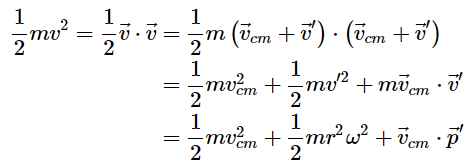
|
212 videos|286 docs|193 tests
|
FAQs on Understanding the Law - Physics for EmSAT Achieve
| 1. How is Newton's Second Law applied to rotation in vector form? |  |
| 2. What is the significance of applying the Rotational Dynamics Equation in understanding Newton's Second Law for Rotation? |  |
| 3. How does Newton's Second Law for Rotation differ from Newton's Second Law for linear motion? |  |
| 4. How can Newton's Second Law for Rotation be applied in real-world scenarios? |  |
| 5. What are some common misconceptions about Newton's Second Law for Rotation? |  |















