Cube Roots of Unity | Mathematics for NDA PDF Download
Cube Root of Unity
There are three cube roots of unity as the name suggests: 1, ω, ω2. Here the roots ω and ω2 are imaginary roots and one root is a square of the other root. The product of the imaginary roots of the cube root of unity is equal to 1(ω · ω2 = ω3 = 1), and the sum of the cube roots of unity is equal to zero.(1 + ω + ω2 = 0).
What is Cube Root Of Unity?
The cube root of unity is represented as ∛1 and it has three roots. The three cube roots of unity are 1, ω, ω2, which on multiplication gives the answer of unity (1). Among the roots of the cube roots of unity, one root is a real root and the other two roots are imaginary roots. The values of the imaginary cube roots of unity are as follows.
- ω = (-1 + i√3) / 2
- ω2 = (-1 - i√3) / 2
Verification of ω and ω2:
Why is (-1 - i√3) / 2 called ω2?
Let's square ω and see what we will get:
ω2 = ω × ω
= [(-1 + i√3) / 2]2
= (-1 + i√3)2 / 4
= (1 + i2 (3) - 2i√3)/4
= (1 - 3 - 2i√3)/4
= (-2 - 2i√3)/4
= (-1 - i√3)/4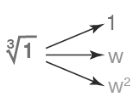
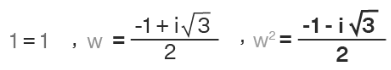
The symbol ω is referred to as omega. Thus, the imaginary cube roots of unity ω, ω2 are read as omega and omega square respectively.
Product of Cube Roots of Unity
The product of the cube roots of unity is equal to 1. This can be understood from the below expression.
1 × ω × ω2 = 1 × (-1 + i√3) / 2 × (-1 - i√3) / 2
= ((-1)2 - (i√3)2) / (2×2)
= (1 - 3i2) / 4
= (1 - 3(-1)) / 4
= 4/4
=1
∴ 1 × ω × ω2 = 1
Sum of Cube Roots of Unity
The sum of the cube roots of unity is equal to zero. This can be observed in the below expression.
1 + ω + ω2 = 1 + (-1 + i√3) / 2 + (-1 - i√3) / 2 = 1 + (-1 + i√3 -1 - i√3) / 2, = 1 + (-2/2) = 1 - 1 = 0
∴ 1+ ω + ω2 = 0
How To Find Cube Root Of Unity?
The cube root of unity can be represented as an expression ∛1 = a, and it has three roots. This expression can be further simplified using algebraic formulas to find the three roots of the cube roots of unity.
∛1 = a
1 = a3
a3 - 1 = 0
By the formula a3 - b3 = (a - b) (a2 + ab + b2),
(a - 1)(a2 + a + 1) = 0
a - 1 = 0 or a = 1
We will solve a2 + a + 1 = 0 by quadratic formula.
a = (-1 ± √(12 - 4(1)(1)) / (2 · 1)
= (-1 ± √(-3)) / 2
= (-1 ± i√3) /2
∴ a = (-1 + i√3) / 2, or (-1 - i√3) / 2
From the above expression, the three cube roots of unity are 1, (-1 + i√3) / 2, and (-1 - i√3) / 2.
Deriving Cube Roots of Unity by De Moivre's Theorem
∛1 can be written as 11/3. In complex numbers, we have a theorem called "De Moivre's theorem" which is very useful in finding the real and complex roots of a real/complex number. This theorem says, (a + ib)n = (r (cos θ + i sin θ))n = rn (cos nθ + i sin nθ), where n ∈ ℤ. Let us assume that a + ib = 1 = 1 + i(0). Then we have a = 1 and b = 0.
Then r = √(a2 + b2) = √(12 + 02) = 1 and θ = tan-1|b/a| = tan-1|0/1| = 0. We can write this angle as 0 + 2nπ, where n = 0, 1, and 2 (since we need to find three roots, 3 integer values are taken for n).
By substituting these values in De Moivre's theorem along with substituting n = 1/3:
(1 + i(0))1/3 = 1 (cos 2nπ + i sin 2nπ)1/3, where n = 0, 1, and 2.
⇒ 11/3 = cos 2nπ/3 + i sin 2nπ/3, where n = 0, 1, and 2.
- When n = 0, 11/3 = cos 0 + i sin 0 = 1 + i(0) = 1.
- When n = 1, 11/3 = cos 2π/3 + i sin 2π/3 = -1/2 + i (√3/2) = (-1 + i√3) / 2 (= ω)
- When n = 2, 11/3 = cos 4π/3 + i sin 4π/3 = -1/2 - i (√3/2) = (-1 - i√3) / 2 (= ω2)
Thus, the cube roots of unity by De Moivre's theorem are 1, (-1 + i√3) / 2, and (-1 - i√3) / 2.
Properties of Cube Root Of Unity
- The cube roots of unity has two imaginary roots (ω, ω2) and one real root (1).
- The sum of the roots of the cube root of unity is equal to zero.(1 + ω + ω2 = 0)
- The square of one imaginary root (ω) of the cube root of unity is equal to another imaginary root(ω2).
- The product of the imaginary roots of the cube roots of unity is equal to 1.(ω × ω2 = ω3 = 1)
Solved Examples
Example 1: Find the value of ω67, using the values of the cube root of unity.
Sol:
ω67 = ω66 + 1
= ω66 × ω1
= (ω3)22 × ω
= 122 × ω
= 1 × ω
= ω
= (-1 + i√3) / 2
Therefore the value of ω67 = (-1 + i√3) / 2.
Example 2: What is the value of the expression of cube root of unity, (1 + ω) + (1 + ω)2 + (1 + ω)3?
Sol:
The given expression is .(1 + ω) + (1 + ω)2 + (1 + ω)3
(1 + ω) + (1 + ω)2 + (1 + ω)3 = (1 + ω) + (1 + 2ω + ω2) + (1 +3ω + 3ω2 + ω3)
= 1 + ω + 1 + 2ω + ω2 + 1 +3ω + 3ω2 + ω3
= 1 + 1 + 1 + ω + 2ω +3ω + ω2 + 3ω2 + ω3
= 3 + 6ω + 4ω2 + ω3
= 3 + 3ω + 3ω2 + 3ω + ω2 + 1
= 3(1 + ω + ω2) + (1 + ω + ω2) + 2ω
= 3(0) + 0 + 2ω
= 0 + 0 + 2ω
= 2ω
Therefore, the result of this expression is 2ω.
|
284 videos|295 docs|232 tests
|
FAQs on Cube Roots of Unity - Mathematics for NDA
| 1. How do you find the cube root of unity? |  |
| 2. What is the significance of the cube root of unity? |  |
| 3. Can you explain the geometric interpretation of the cube roots of unity? |  |
| 4. How are the cube roots of unity related to trigonometry? |  |
| 5. How can the cube roots of unity be used in solving equations and problems in mathematics? |  |
















