Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Ratios
Ratios | Mathematics for GCSE/IGCSE - Class 10 PDF Download
What is a ratio?
- A ratio is a method of comparing one part of a whole to another
- A ratio can be represented as a fraction (of the whole)
- Ratios are commonly used when illustrating how things are divided or in situations involving scale factors
- For instance, if a pizza is divided into 8 slices and shared in the ratio 6:2, it implies that person A gets 6 slices, and person B gets 2 slices
How do I simplify a ratio or find an equivalent ratio?
- When we talk about ratios, we are essentially comparing two quantities. For instance, if we have a pizza cut into 8 slices and they are shared in the ratio 6:2, we are comparing the amounts received by two individuals.
- It's important to understand that ratios can be simplified. For example, the ratio 6:2 can also be expressed as 3:1 by dividing both sides of the ratio by 2. This simplification does not change the relative amounts each person receives.
- Simplifying ratios is akin to simplifying fractions. Just like 1/2 is equivalent to 2/4, the ratio 6:2 is equivalent to 3:1. The key is to ensure that the ratio's proportions remain the same.
- When determining an equivalent ratio, it involves either multiplying or dividing both sides of the ratio by the same number.
- For example, consider a giant pizza cut into 800 slices. Person A might get 600 slices, while Person B would receive 200 slices. In this scenario, both sides of the ratio have been scaled by a factor of 100.
- Scaling ratios is a flexible process. It allows us to maintain proportionality, such as ensuring that Person A consistently receives three times the amount that Person B receives.
- Scaling ratios is akin to finding equivalent fractions or simplifying them. However, it's crucial to note that a ratio like 1:4 is not the same as 1/4.
How do I use a ratio to find a fraction?
- Ratios can be used to calculate a fraction of a total amount.
- For instance, if 8 pizza slices are shared in the ratio 6:2, Person A would receive 6 out of 8 slices, which is 6/8 or 3/4 of the pizza.
- Similarly, Person B would get 2 out of 8 slices, which is 2/8 or 1/4 of the pizza.
- These fractions can be converted to percentages if necessary.
Working with Ratios
How do I share an amount into a ratio?
- If we have $200 to divide between individuals A and B in the ratio 5:3
- This ratio translates to a total of 8 parts, with A receiving 5 parts and B receiving 3 parts
- To split $200 into 8 parts, each part is valued at $25 ($200 ÷ 8 = $25)
- Illustrating this division with a simple diagram can aid understanding:
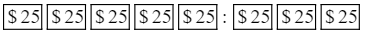
- Person A gets 5 parts, each valued at $25, totaling $125 for person A (5 × 25 = $125)
- Person B gets 3 parts, each valued at $25, totaling $75 for person B (3 × 25 = $75)
- Ensure that the sum of the amounts for each person equals the total amount: $125 + $75 = $200
What do I do when given the difference in a ratio problem?
- When faced with a scenario involving ratios, rather than being provided with the total quantity, you might be given the discrepancy between two separate shares.
- For instance, consider a situation in a parking lot where the ratio of blue cars to silver cars is 3:5, with the added information that there are 12 more silver cars than blue cars.
- Some students find it helpful to show this in a simple diagram

- The difference in the number of parts of the ratio is 2 (5 – 3 = 2)

- The difference in the number of cars is 12
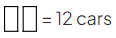
- This means that 2 parts = 12 cars
- We can simplify this to 1 part = 6 cars (by dividing both sides by 2)
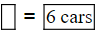
- Now that we know how much 1 part is worth, we can find how many cars of each colour there are, and the total number of cars

- 3 parts are blue
3 × 6 = 18 blue cars - 5 parts are silver
5 × 6 = 30 silver cars 8 parts in total
8 × 6 = 48 cars in total
- 3 parts are blue
Given one part of a ratio, how can I find the other part?
- Instead of being provided with the total quantity to be divided, you might be given the value of one side of the ratio.
- For instance, consider a fruit drink prepared by blending concentrate with water in the ratio 2:3. We aim to determine the volume of water required to be added to 5 litres of concentrate.
- Some students find it helpful to show this in a simple diagram

- We are told that there are 5 litres of concentrate, and it must be mixed in the ratio 2:3
- This means that the two parts on the left, are equivalent to 5 litres
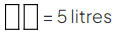
- This means that 1 part must be equal to 2.5 litres (5 ÷ 2 = 2.5)
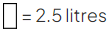
- Now that we know how much 1 part is worth, we can find how many litres of water are required, and the total amount of fruit drink produced

3 parts are water3 × 2.5 = 7.5 litres of water
5 parts in total
5 × 2.5 = 12.5 litres of fruit drink produced in total
How do I combine two ratios to make a 3-part ratio?
- Consider a scenario where you are presented with two distinct ratios that interconnect, forming a 3-part ratio.
- Imagine a farm housing a total of 85 animals.
- Ratio of cows to sheep: 2:3
- Ratio of sheep to pigs: 6:7
- Objective: Determine the quantity of each animal on the farm.
- Directly distributing 85 animals based on the ratios 2:3 or 6:7 isn't feasible as these ratios do not encompass all the animals independently.
- It's necessary to establish a consolidated, 3-part ratio illustrating the proportional shares of all animals collectively.
- Key Insight: Leveraging the common entity, sheep, in both ratios as a connecting link.
- Given C:S = 2:3 and S:P = 6:7, scale the C:S ratio by 2 to standardize both ratios concerning 6 sheep.
- Resulting in C:S = 4:6 and S:P = 6:7, which can be amalgamated into a comprehensive ratio, C:S:P = 4:6:7.
- Allocation of Animals
- Utilize the unified ratio 4:6:7 to apportion the 85 animals accordingly.
- With a total of 17 parts (4 + 6 + 7 = 17) in the ratio, each part corresponds to 5 animals (85 ÷ 17 = 5).
- Consequently, there are 20 cows (4 x 5), 30 sheep (6 x 5), and 35 pigs (7 x 5) on the farm.
Question for RatiosTry yourself: When dividing a pizza into 8 slices and sharing in the ratio 6:2, how many slices does person A receive?View Solution
The document Ratios | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
66 videos|674 docs|19 tests
|
FAQs on Ratios - Mathematics for GCSE/IGCSE - Class 10
| 1. What is a ratio? |  |
Ans. A ratio is a comparison of two quantities that shows how many times one quantity is contained within another. It is typically written in the form of a fraction or with a colon between the two numbers.
| 2. How are ratios used in mathematics? |  |
Ans. Ratios are used in mathematics to compare quantities, make predictions, solve problems involving proportions, and understand relationships between different values.
| 3. Can ratios be simplified? |  |
Ans. Yes, ratios can be simplified by dividing both numbers by their greatest common factor to obtain an equivalent ratio with smaller numbers.
| 4. What is the difference between a ratio and a proportion? |  |
Ans. A ratio compares two quantities, while a proportion is an equation that states two ratios are equal. In other words, a proportion is a statement that two ratios are equivalent.
| 5. How can ratios be used in everyday life? |  |
Ans. Ratios can be used in everyday life to compare prices, calculate ingredients in a recipe, determine distances on a map, and analyze financial statements, among other applications.
Related Searches
















