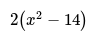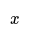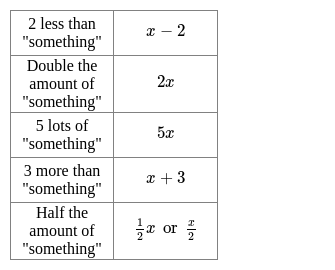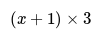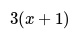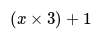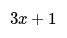Forming & Solving Equations - Year 11 PDF Download

CIE IGCSE Maths: Extended

Revision Notes

Syllabus Edition

First teaching 2023

First exams 2025

Forming Equations

Forming Equations

Before solving an equation you may need to form it from the information given in the question.

• Paraphrasing Information

  Take the given information and restate it in your own words to create the equation.

• Elaboration with Examples

  Provide detailed explanations and examples to ensure understanding.

• Bullet Points Importance

  Use bullet points to highlight key details and make the content more digestible.

• Clarity in Expression Formation

  Ensure that the equation formed is clear and accurately represents the given information.

Understanding Expressions in Algebra

• An expression in algebra is a mathematical statement that doesn't have an equals sign, like "2x + 3" or "y - 5".
• Expressions are useful for representing unknown values in mathematical problems.
• When an unknown value needs to be represented, it can be denoted by a letter, such as "x" or "y".
• Common phrases can be translated into expressions by assigning variables to the unknowns.
• Using brackets can help indicate the correct order of operations within an expression.
• For example, "something add 1 then multiplied by 3" can be written as "3(something + 1)".
• It's important to choose the smallest value possible to represent a letter in an expression for simplicity.
• If Adam is 10 years younger than Barry, and we represent Adam's age as "x", then Barry's age can be represented as "x + 10".
• If Adam's age is half of Barry's age, and we represent Adam's age as "y", then Barry's age can be represented as "2y".

Illustrative Examples

Understanding Age Relationships: Adam and Barry

• If Adam is 10 years younger than Barry, then Barry is 10 years older than Adam. Represent Adam's age as x, then Barry's age is x + 10. This simplifies algebraic expressions.
• If Adam's age is half of Barry's age, then Barry's age is double Adam's age. So if Adam's age is x, then Barry's age is 2x. This simplifies the algebraic expressions further.

How to Form an Equation?

To create an equation based on the given information, follow these steps:

• Identify the relationship between Adam and Barry's ages.
• Assign a variable to represent one of their ages.
• Express the other age in terms of the variable.
• Set up the equation based on the given conditions.

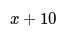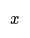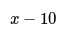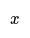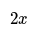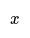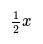An Equation Explained

• An equation is a mathematical expression containing an equals sign that can be solved to find the value of the variable.
• To solve an equation, you first create an expression and set it equal to a specific value or another expression.
• It's beneficial to be familiar with alternative terms for basic operations:
  • Addition: sum, total, more than, increase, etc.
  • Subtraction: difference, less than, decrease, etc.
  • Multiplication: product, lots of, times as many, double, triple, etc.
  • Division: shared, split, grouped, halved, quartered, etc.
• For instance, in a scenario where Adam is 10 years younger than Barry and their combined age is 25, you can determine their individual ages by setting up and solving an equation.

Understanding Equations

• An equation is a fundamental mathematical concept involving an equals sign for solving unknown values.
• When encountering equations, it's essential to create expressions and equate them to solve for variables.

Problem Solving with Equations

• If we have two individuals, Adam and Barry, with a specific age relationship, we can represent their ages using equations.
• Let's say Adam is 10 years younger than Barry and the sum of their ages is 25. To find their ages, we can set up the following equation: Adam's age + Barry's age = 25.

• We can then solve this equation to determine Adam's and Barry's ages.

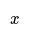
Simultaneous Equations

• Sometimes, we encounter situations where we have two unknown values (x and y) and need to create two simultaneous equations to solve for them.
• For instance, consider a scenario where the prices of a child's ticket and an adult's ticket at a theatre are given.

• We can write equations based on the given information to represent the relationship between the prices of adult and child tickets.
• For example:
  • a) Adult price = 2 x Child price
  
  • b) Another representation: Adult price = Child price + $7
  
  • c) Total cost equation: 3 x Child price + 2 x Adult price = $45

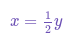
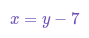
Forming Equations from Shapes

Many questions involve having to form and solve equations from information given about things relating to shapes, like lengths or angles.

• Rectangles:
• To find the perimeter of a rectangle, add up all the sides: Perimeter = 2 * (length + width)
• To find the area of a rectangle, multiply the length by the width: Area = length * width
• Squares:
• The perimeter of a square is four times the length of one side: Perimeter = 4 * side length
• The area of a square is the side length squared: Area = side length * side length
• Triangles:
• To find the perimeter of a triangle, add the lengths of all three sides.
• The area of a triangle is calculated using the formula: Area = 0.5 * base * height
• Circles:
• The circumference of a circle is given by: Circumference = 2 * π * radius
• The area of a circle is: Area = π * radius^2

Strategies for Solving Geometry Problems

• When faced with a geometry problem, start by carefully reading the question to determine if it involves area, perimeter, or angles.
• If a diagram is not provided, it is advisable to quickly sketch one as it can provide valuable visual cues.
• Include any information provided in the question onto the diagram, usually in the form of expressions involving one or two variables.
• For perimeter-related questions, identify which sides have equal lengths and sum them up. Consider the shape's properties to determine side equality.
• In shapes like squares or rhombuses, all sides are equal; in rectangles or parallelograms, opposite sides are equal. For triangles, check for sides of equal length.
• For questions involving area, jot down the necessary formula for the area of the given shape. If the shape is uncommon, break it down into simpler shapes to calculate their areas.
• Remember, a regular polygon has all sides of equal length. For example, a regular pentagon with side length 2x - 1 has 5 equal sides, making its perimeter 5(2x - 1).
• If dealing with a circle or a part of it, use the constant π consistently instead of multiplying by it, preventing long decimals in your calculations.

Key Steps to Tackle Geometry Problems

• Always begin by analyzing the question to discern the type of geometric problem you are solving: area, perimeter, or angles.
• Sketch a diagram promptly if one is not provided to enhance your understanding of the problem.
• Transfer any relevant data from the question onto your diagram, typically involving algebraic expressions with variables.
• When addressing perimeter queries, identify and combine sides of equal length based on the characteristics of the shape. Remember the unique properties of different geometric figures.

Geometric Shapes and Formulas

• In a square or rhombus, all four sides are equal
• In a rectangle or parallelogram, opposite sides are equal
• If a triangle is given, check if any of the sides are equal in length

Calculating Area of Shapes

• If the question involves area, write down the necessary formula for the area of that shape
• If it is an uncommon shape, consider splitting it into two or more common shapes to find the areas
• Remember to split the length and width accordingly for calculations

• If it is an uncommon shape, consider splitting it into two or more common shapes to find the areas

Special Considerations for Regular Polygons

• Regular polygons have all sides of equal length
• For example, a regular pentagon with side length 2x – 1 has 5 equal sides, making its perimeter 5(2x – 1)

• For example, a regular pentagon with side length 2x – 1 has 5 equal sides, making its perimeter 5(2x – 1)

Forming Equations with Angles in 2D Shapes

#Paraphrase the information given, elaborate, and explain with examples wherever required. Present all points in bullet format with proper headings. Ensure language is easy to understand.

Sum of Angles in Polygons

• For a polygon of n sides, the sum of the angles will be 180°×(n - 2). Remember that a regular polygon means all the angles are equal.
• If a question involves an irregular polygon, assume all the angles are different unless told otherwise.
• Look out for key information that can give more information about the angles.
• For example, a trapezium "with a line of symmetry" will have two pairs of equal angles.

Angles in Polygons Details

• For a polygon of n sides, the sum of the angles will be 180°×(n - 2).
• Remember that a regular polygon means all the angles are equal.
• If a question involves an irregular polygon, assume all the angles are different unless told otherwise.
• Look out for key information that can give more information about the angles.
• For example, a trapezium "with a line of symmetry" will have two pairs of equal angles.

Forming Equations for 3D Shapes

• How do I form an equation involving the surface area or volume of a 3D shape?

• Paraphrase the information given, elaborate, and explain with examples wherever required.
• Give all points in bullet format with proper headings.
• Make sure not more than 2 headings have an HTML tag H7 and not more than 4 subheadings have an HTML tag H8; otherwise, make the headings bold.
• Make sure everything is paraphrased and in detail and keep the language easy to understand.

Optimizing Learning in Geometry: Surface Area and Volume

• Read the question carefully to determine if it involves surface area or volume.
• Mixing these up is a common error observed in GCSE exams.
• If a diagram is not provided, consider sketching a quick one for clarity.
• Include any provided information from the question in your diagram.
• This information typically includes expressions involving one or two variables.
• Examine the properties of the given shape to identify sides with equal lengths.
• In a cube, all sides are equal; all prisms share the same cross-sectional shape at the front and back.
• Pyramids commonly incorporate the factor 1/3 in their formulae.
• If the problem pertains to volume, jot down the requisite formula for the shape's area.
• If the shape is unconventional, the exam question will provide the necessary formula. Sub in expressions for side lengths into the formula, ensuring bracketed expressions are correctly substituted.
• If surface area is the focus:
• Write down the number of faces the shape has and identify any identical ones.
• Determine the 2D shape of each face, noting down the area formula for each.
• Substitute the given expressions into the appropriate formula for each face, ensuring accurate dimension identification. Adjust expressions as needed.
• Compute the total area by summing up all expressions, ensuring each face is considered, even hidden ones in the diagram.

Step-by-Step Guide for Calculating the Perimeter of a Rectangle

• Write down the number of faces the shape has and identify if any are the same.
• Identify the 2D shape of each face and note down the formula for the area of each one.
• Substitute the given expressions into the formula for each face, ensuring the correct dimensions are used.
• You may need to add or subtract some expressions.
• Add the expressions together, ensuring one expression for each face is accounted for.
• Remember to consider any hidden faces in the diagram.
• Use a pencil to carefully annotate the diagrams.
• Most of the work for a question may involve the diagram itself.
• Always read the question carefully - for instance, find the area if asked for, not the perimeter; find the volume if it asks for surface area, etc.

Calculation Example for a Rectangle

Consider a rectangle with a length of 3 cm and a width of 1 cm.

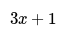
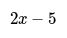
The rectangle's perimeter is given as 22 cm.

The formula for the perimeter of a rectangle is P = 2(length) + 2(width).

Substitute the values: P = 2(3) + 2(1).

Expanding and Simplifying Equations

• Expand the brackets: When we have an expression like P = 2(3x - 1) + 2(2x - 5), we distribute the values inside the brackets to simplify it. The expanded form of this expression is 6x - 2 + 4x - 10.
• Simplify the expression: By combining like terms, the simplified form of the expression becomes 10x - 12.
• Setting it equal to the perimeter: If the perimeter is given as 22, we equate the expression to 22 and solve for x.
• Solving for x: By solving the equation 10x - 12 = 22, we find that x = 3.

Further Steps:

• Adding 4 to both sides: To isolate x, we add 4 to both sides of the equation 10x - 12 = 22. This results in the equation 10x = 26.
• Dividing both sides by 5: By dividing both sides by 5, we find the value of x to be x = 3.

Test yourself

Next topic

Download notes on Forming Equations