Double Century Chapter Notes | Mathematics for Class 3 (Maths Mela) PDF Download
| Table of contents |

|
| Ancient Methods of Counting |

|
| Making 100 |

|
| Counting After 100 |

|
| Number Names |

|
| Let's Learn Names! |

|
| Let's Learn Combinations! |

|
| Let's Practice! |

|

A long time ago, people did not have number symbols like we do today. Instead, they made little marks on cave walls and tree bark to count things. Now, we use just ten digits—0, 1, 2, 3, 4, 5, 6, 7, 8, and 9—to write any number, big or small. Let’s see how this amazing system works!
Ancient Methods of Counting
Counting with Groups
- Long ago, people counted things by grouping them into 5s, 10s, 20s, or even 60s. This made it easier to keep track of their things and trade with others.
- Thousands of years ago, ancient Indians created a special system using just ten digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. This was one of the greatest inventions in history!
- Thanks to this number system, we now have TVs, computers, mobile phones, and many other technologies!
The Importance of Zero
- A long time ago, people had no way to write "nothing." Then, they invented zero (0)!
- This small number made a big difference! It helped make counting and math easier. Because of zero, we can do big calculations and solve tricky problems.

Now, this number system is used all over the world!
Sachin’s 99→100 Surprise
One day, Sachin’s homework was to add 1 to every number:- 1 + 1 = 2
- 2 + 1 = 3
- 23 + 1 =24
- 56 + 1 = 57
- … he kept going until he saw 99 + 1 = ?
Sachin scratched his head.
Just then his brother Vivek popped in.

Vivek: “What’s up, Sachin?”
Sachin: “I’m stuck at 99—what comes next?”
Vivek: “Easy—100!”
Sachin’s eyes lit up: “Oh—I get it now! 99 + 1 is 100!”
Vivek (smiling): “Numbers keep going forever. There’s always more to learn!”
Making 100
In math, we can make 100 in different ways by adding two numbers together. Let's look at some examples:

- 90 + 10 = 100
- 80 + 20 = 100
- 70 + 30 = 100
- 60 + 40 = 100
- 50 + 50 = 100
This means there are many ways to make 100.
Using Matchsticks to Make 100
We can also use matchsticks to understand numbers.
If we take 10 bundles of matchsticks, with 10 sticks in each bundle, we get 100 matchsticks in total.
 Try this:
Try this:
- Count 10 matchsticks and make a bundle.
- Keep making bundles until you have 100 matchsticks.
- How many bundles do you need? (Answer: 10)

You can also try this with seeds, beads, or buttons to practice counting and making 100 in different ways.
Let's Learn by Practicing
Tanya and Reema, two friends who loved math, found a fun game one day. Tanya had learned in class how to make 100 by adding different numbers together. She was excited to share it with Reema.
 Tanya & Reema
Tanya & Reema
- Tanya excitedly explained, "We can write down any five numbers between 1 and 99. Then, I'll add another number to yours to make it 100!"
- Reema smiled and wrote down her five numbers: 20, 35, 42, 68, and 75.
- Tanya smiled and said, "Let's begin!" She took Reema's first number, 20, and added 80 to it, making it 100. "20 + 80 = 100!"
- Next, she looked at 35, added 65, and said, "35 + 65 = 100!"
- They kept playing, mixing numbers in fun ways. Tanya added 58 to 42, 32 to 68, and 25 to 75, making each one equal 100.
Exploring Other Ways to Make 100

- Besides the combinations Tanya made, we can use matchstick bundles and a number line to visualise making 100 in various ways. For example, using 10 matchsticks for tens and 1 for units can help us understand reaching 100.
- We can also estimate the number of objects, like oranges or bangles, to see how they can be grouped to make 100. This estimation improves our understanding of quantities.
- Another fun game involves using claps, snaps, and pats to represent numbers. For example, one clap could mean 100, one snap could mean 10, and one pat could mean 1. This interactive game aids in visualising numbers and their combinations.
- Just like the combinations Tanya made, many other ways exist to make 100 using different numbers. Let's keep exploring creative number combinations!

Counting After 100
After reaching 100, counting continues in a similar way. Here's how it works:
1. Using Hundreds:

- 100 + 1 = 101 (One Hundred One)
- 100 + 2 = 102 (One Hundred Two)
- 100 + 3 = 103 (One Hundred Three)
2. Hundreds and Tens:
- 100 + 10 = 110 (One Hundred Ten)
- 100 + 20 = 120 (One Hundred Twenty)
- 100 + 30 = 130 (One Hundred Thirty)
3. Hundreds and Ones:
- 100 + 5 = 105 (One Hundred Five)
- 100 + 8 = 108 (One Hundred Eight)
- 100 + 15 = 115 (One Hundred Fifteen)
To express numbers beyond 100, we use ten symbols (0-9) which help us write all numbers, where each place value (hundreds, tens, ones) is important in forming these numbers.
Number Names
Understanding Numbers Beyond 100

- Just as numbers below 100 have names, numbers above 100 do too.
- We will look at how these number names are structured.
Understanding 100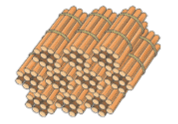
- Are these 100?
Yes, 10 bundles of 10 sticks make one bundle of 100.
Let's Learn Names!
Once upon a time, there was a boy named Rahul who loved to learn new things. One day, he wanted to learn the names of numbers above 100, but he found it a bit difficult. He struggled to say numbers like 101, 105, or 110.
Names of Numbers Above 100
 Rahul & Anju
Rahul & Anju
- Rahul felt a bit frustrated, but then his older sister Anju noticed his confusion. Anju was great at explaining things simply.
- Anju sat down with Rahul and said, "Let me show you how to name numbers above 100, Rahul. It's easy!"
- She started with 100 and explained, "When we have 100 and add 1, it becomes One Hundred One. We just say 'One Hundred' and then add the next number."

- Rahul's eyes lit up with understanding. "Oh, so 100 and 2 is One Hundred Two, right?"
- Anju nodded, "Exactly! You're getting it."
- Next, she showed him 100 and 5, saying, "When we have 100 and add 5, it's One Hundred Five.
- Then she explained, "100 and 9 make One Hundred Nine. "
- Finally, she said, "And 100 and 10 makes One Hundred Ten."
Examples
- 109 - One Hundred Nine
- 123 - One Hundred Twenty Three
- 150 - One Hundred Fifty
- 157 - One Hundred Fifty Seven
- 159 - One Hundred Fifty Nine
Explanation
- 109 - Here we have a Hundred and a Nine, so its name will be One Hundred Nine.
- 123 - One Hundred + Twenty Three = One Hundred Twenty Three
- 150 - One Hundred + Fifty = One Hundred Fifty
- 157 - One Hundred + Fifty Seven = One Hundred Fifty Seven
- 159 - One Hundred + Fifty Nine = One Hundred Fifty Nine
From that day on, Rahul was confident in naming numbers above 100, thanks to his sister's clear explanations and patient teaching.
Let's Learn Combinations!
Once upon a time, there was a clever little dog named Bingo. Bingo loved playing with numbers. One day, he decided to help his friends learn how to add numbers to reach a target by inviting them to a fun game.
Bingo said, "Just like Bingo and his friends, you can also try more examples to understand how numbers work. Our first goal is to make 100."
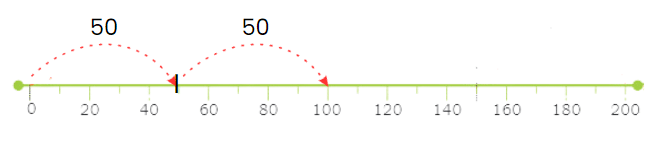
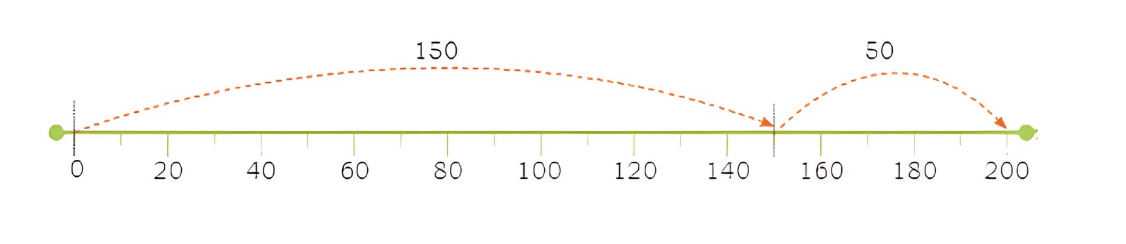
Bingo pointed to the number line and asked, "If we start with 50, what can we add to make 100?" His friends thought for a moment and shouted, "50! Because 50 + 50 equals 100!" Bingo wagged his tail happily.
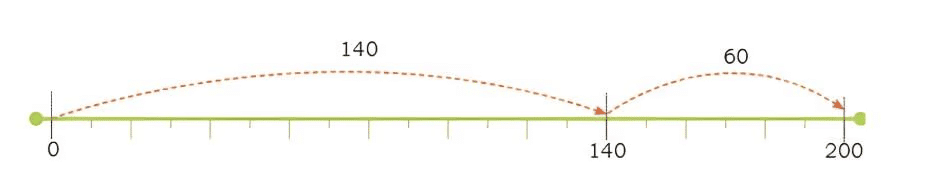
Bingo continued, "How about making 200?" One friend replied, "We can add 140 and 60 because 140 + 60 equals 200!" Bingo smiled and explained, "You could also add 150 and 50 or 120 and 80. See how many ways we can reach our goal?"
Exploring Combinations
- 60 and 40 make 100
- 45 and 55 make 100
Bingo clapped his paws and said, "Great job, everyone! You’ve learned to add numbers to make bigger numbers!"
Now, let us play a game called "Clap, Snap, and Pat." One clap represents 100, one snap represents 10, and one pat represents 1. You can play this game in teams where one team shows a number using claps, snaps, and pats, and the other team guesses it.
And so, Bingo and his friends kept playing with numbers, learning new ways to add and reaching their target goals. They had so much fun learning together!
Just like Bingo and his friends, you can also try some more examples and understand how numbers work.
Let's Practice!
Question 1:
Write numbers in the blank spaces inside the flower petals so that the numbers in each petal add up to 100. 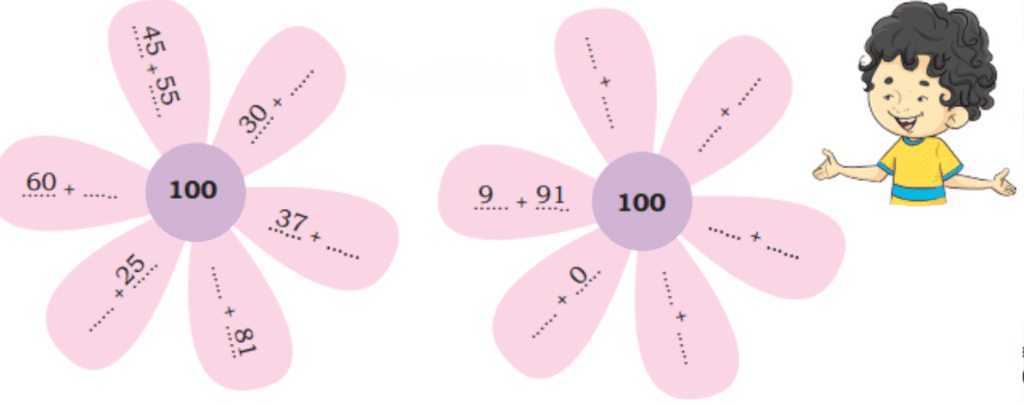
 View Answer
View Answer 
Answer: 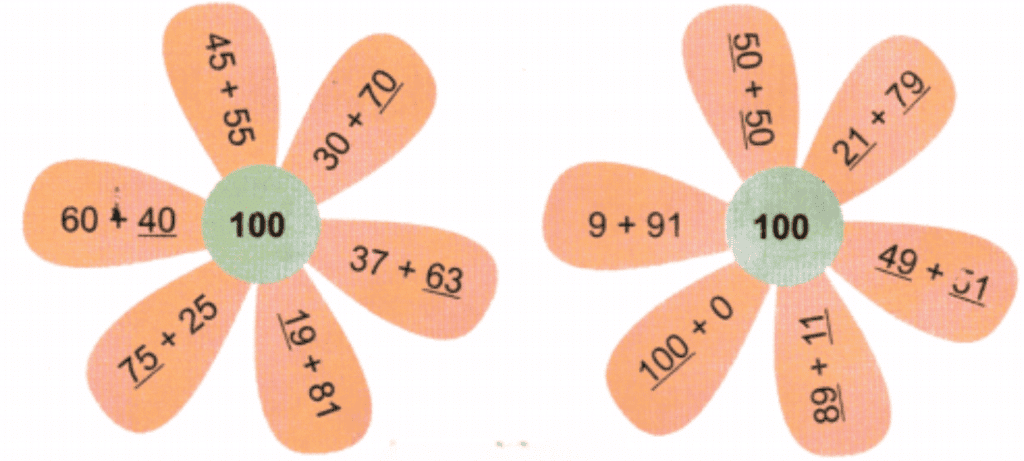
Question 2:
Look at the picture. Estimate and write the number of each of the following objects.

a. Oranges: …………..
b. Bangles: ………….
c. Laddoos: …………
d. Barfi :……………
e. Bindis: ……………
f. Bananas: …………………
 View Answer
View Answer 
Answer:
Number of each of the following objects:
(a) Oranges : 22
(b) Bangles : 75
(c) Laddoos : 28
(d) Barfi : 22
(e) Bindis : 80
(f) Bananas : 36
|
26 videos|180 docs|28 tests
|
FAQs on Double Century Chapter Notes - Mathematics for Class 3 (Maths Mela)
| 1. What are some ancient methods of counting discussed in the article? |  |
| 2. How can I help my child practice making combinations of numbers? |  |
| 3. What strategies are suggested for counting numbers beyond 100? |  |
| 4. What are the importance and methods of learning number names in early education? |  |
| 5. How can the concept of making 100 be taught effectively to children? |  |





















