Important Formulas: Trigonometry | Quantitative Aptitude (Quant) - CAT PDF Download
Trigonometry formulas are equations that relate the sides and angles of triangles. They are essential for solving a wide range of problems in mathematics, physics, engineering and other fields.
Here are some of the most common types of trigonometry formulas:
- Basic definitions: These formulas define the trigonometric ratios (sine, cosine, tangent, etc.) in terms of the sides of a right triangle.
- Pythagorean theorem: This theorem relates the lengths of the sides in a right triangle.
- Angle relationships: These formulas relate the trigonometric ratios of different angles, such as sum and difference formulas, double angle formulas, and half angle formulas.
- Reciprocal identities: These formulas express one trigonometric ratio in terms of another, such as sin(θ) = 1/coc(θ).
- Unit circle: The unit circle is a graphical representation of the trigonometric ratios, and it can be used to derive many other formulas.
- Law of sines and law of cosines: These laws relate the sides and angles of any triangle, not just right triangles.
Read on to learn about different trigonometric formulas and identities, solved examples, and practice problems.
What is Trigonometry?
- Trigonometry is defined as a branch of mathematics that focuses on the study of relationships involving lengths and angles of triangles.
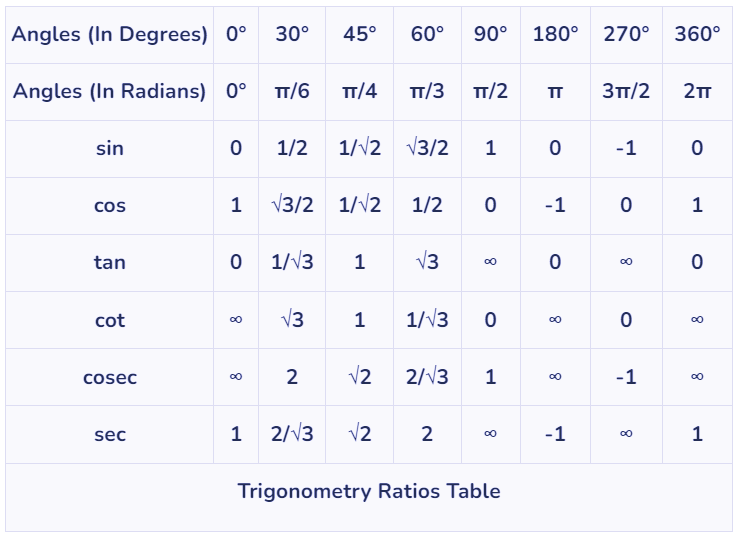
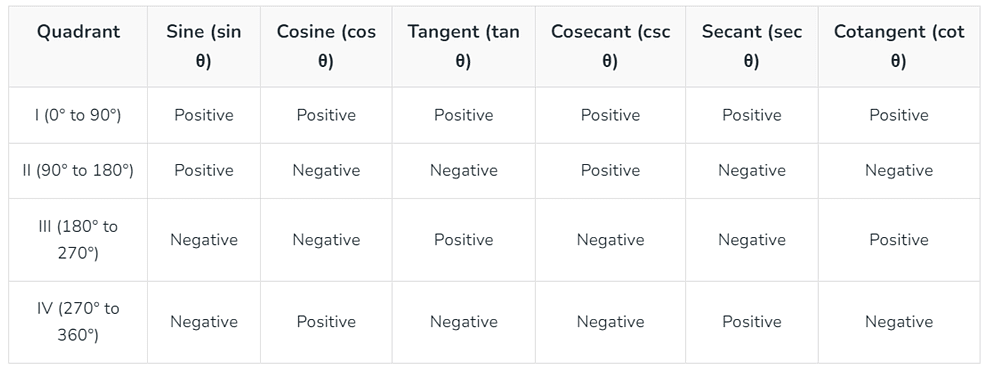
- Following are the values of all 6 trigonometric ratios on different angles
Trigonometry Functions
Trigonometric functions are mathematical functions that relate angles of a right triangle to the lengths of its sides. They have wide applications across various fields such as physics, engineering, astronomy, and more. The primary trigonometric functions include sine, cosine, tangent, cotangent, secant, and cosecant.
Trigonometry Formula Overview
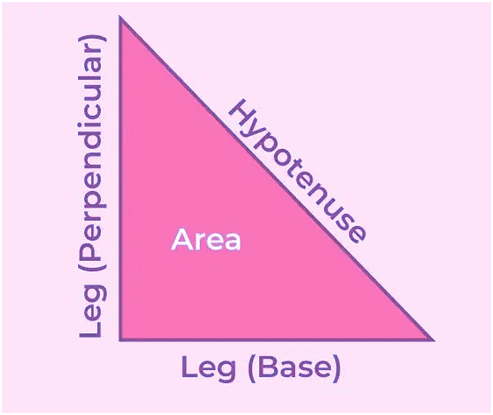
Trigonometry formulas are mathematical expressions that relate the angles and sides of a Right Triangle. There are 3 sides a right-angled triangle is made up of:
- Hypotenuse: This is the longest side of a right-angled triangle.
- Perpendicular/Opposite side: It is the side that forms a right angle with respect to the given angle.
- Base: The base refers to the adjacent side where both the hypotenuse and the opposite side are connected.
 All the trigonometric ratios, product identities, half angle formulas, double angle formulas, sum and difference identities, cofunction identities, a sign of ratios in different quadrants, etc. are briefly given here for the students of Classes 9, 10, 11, 12.
All the trigonometric ratios, product identities, half angle formulas, double angle formulas, sum and difference identities, cofunction identities, a sign of ratios in different quadrants, etc. are briefly given here for the students of Classes 9, 10, 11, 12.
Here is the list of formulas in trigonometry we are going to discuss:
- Basic Trigonometric Ratio Formulas
- Unit Circle Formulas
- Trigonometric Identities
Basic Trigonometric Ratios
There are 6 ratios in trigonometry. These are referred to as Trigonometric Functions. Below is the list of trigonometric ratios, including sine, cosine, secant, cosecant, tangent and cotangent.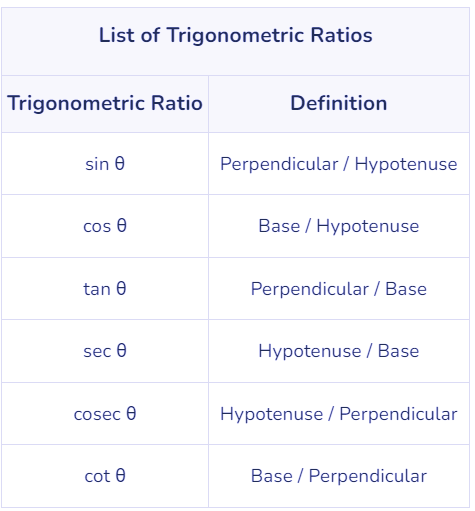
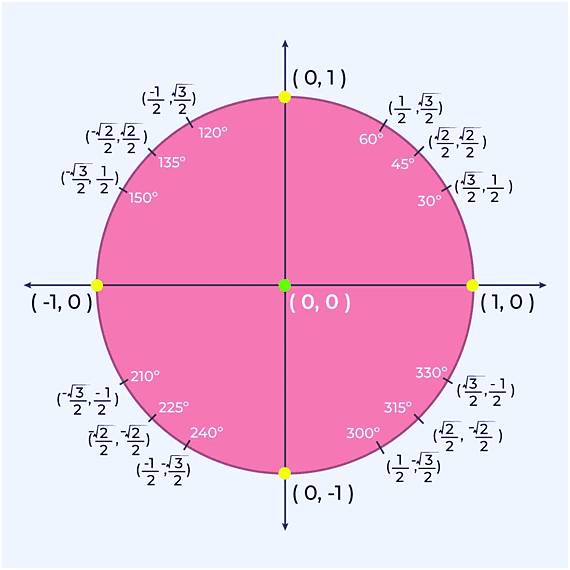
Unit Circle Formula in Trigonometry
For a unit circle, for which the radius is equal to 1, θ is the angle. The values of the hypotenuse and base are equal to the radius of the unit circle.
Hypotenuse = Adjacent Side (Base) = 1
The ratios of trigonometry are given by:
- sin θ = y/1 = y
- cos θ = x/1 = x
- tan θ = y/x
- cot θ = x/y
- sec θ = 1/x
- cosec θ = 1/y

Trigonometric Identities
The relationship between trigonometric functions is expressed via trigonometric identities, sometimes referred to as trig identities or trig formulae. They remain true for all real number values of the assigned variables in them.
1. Reciprocal Identities
All of the reciprocal identities are obtained using a right-angled triangle as a reference. Reciprocal Identities are as follows:
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
2. Pythagorean Identities
According to the Pythagoras theorem, in a right triangle, if ‘c’ is the hypotenuse and ‘a’ and ‘b’ are the two legs then c2 = a2 + b2. We can obtain Pythagorean identities using this theorem and trigonometric ratios. We use these identities to convert one trig ratio into other.
- sin2θ + cos2θ = 1
- 1 + tan2θ = sec2θ
- 1 + cot2θ = cosec2θ
3. Periodicity Identities (in Radians)
These identities can be used to shift the angles by π/2, π, 2π, etc. These are also known as co-function identities.
All trigonometric identities repeat themselves after a particular period. Hence are cyclic in nature. This period for the repetition of values is different for different trigonometric identities.
- sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
- sin (π/2 + A) = cos A & cos (π/2 + A) = – sin A
- sin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A
- sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A
- sin (π – A) = sin A & cos (π – A) = – cos A
- sin (π + A) = – sin A & cos (π + A) = – cos A
- sin (2π – A) = – sin A & cos (2π – A) = cos A
- sin (2π + A) = sin A & cos (2π + A) = cos A
 4. Even and Odd Angle Formulas
4. Even and Odd Angle Formulas
The Even and Odd Angle Formulas , also known as Even-Odd Identities are used to express trigonometric functions of negative angles in terms of positive angles. These trigonometric formulas are based on the properties of even and odd functions.
- sin(-θ) = -sinθ
- cos(-θ) = cosθ
- tan(-θ) = -tanθ
- cot(-θ) = -cotθ
- sec(-θ) = secθ
- cosec(-θ) = -cosecθ
5. Cofunction identities (in Degrees)
Cofunction identities give us the interrelationship between various trigonometry functions. The co-function are listed here in degrees:
- sin(90°−x) = cos x
- cos(90°−x) = sin x
- tan(90°−x) = cot x
- cot(90°−x) = tan x
- sec(90°−x) = cosec x
- cosec(90°−x) = sec x
6. Sum and Difference Identities
The sum and difference identities are the formulas that relate the sine, cosine, and tangent of the sum or difference of two angles to the sines, cosines, and tangents of the individual angles.
- sin(x+y) = sin(x)cos(y) + cos(x)sin(y)
- sin(x-y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x+y) = cos(x)cos(y) – sin(x)sin(y)
- cos(x-y)=cos(x)cos(y) + sin(x)sin(y
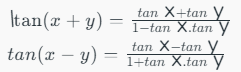
7. Double Angle Identities
Double angle identities are the formulas that express trigonometric functions of angles which are double the measure of a given angle in terms of the trigonometric functions of the original angle.
- sin (2x) = 2sin(x)
- cos(x) = [2tan x/(1 + tan2 x)]
- cos (2x) = cos2(x) – sin2(x) = [(1 – tan2 x)/(1 + tan2 x)] = 2cos2(x) – 1 = 1 – 2sin2(x)
- tan (2x) = [2tan(x)]/ [1 – tan2(x)]
- sec (2x) = sec2 x/(2 – sec2 x)
- cosec (2x) = (sec x • cosec x)/2
8. Inverse Trigonometry Formulas
Inverse trigonometry formulas relate to the inverse trigonometric functions, which are the inverses of the basic trigonometric functions. These formulas are used to find the angle that corresponds to a given trigonometric ratio.
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – cos-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
9. Triple Angle Identities
Triple Angle Identities are formulas used to express trigonometric functions of triple angles (3θ) in terms of the functions of single angles (θ). These trigonometric formulas are useful for simplifying and solving trigonometric equations where triple angles are involved.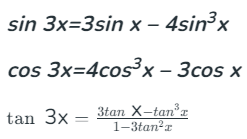
10. Half Angle Identities
Half-angle identities are those trigonometric formulas that are used to find the sine, cosine, or tangent of half of a given angle. These formulas are used to express trigonometric functions of half-angles in terms of the original angle.
11. Sum to Product Identities
Sum to Product identities are the trigonometric formulas that help us to express sums or differences of trigonometric functions as products of trigonometric functions.
- sinx + siny = 2[sin((x + y)/2)cos((x − y)/2)]
- sinx − siny = 2[cos((x + y)/2)sin((x − y)/2)]
- cosx + cosy = 2[cos((x + y)/2)cos((x − y)/2)]
- cosx − cosy = −2[sin((x + y)/2)sin((x − y)/2)]
12. Product Identities
Product identities, also known as product-to-sum identities are the formulas that allow the expression of products of trigonometric functions as sums or differences of trigonometric functions.
These trigonometric formulas are derived from the sum and difference formulas for sine and cosine.
- sinx⋅cosy = [sin(x + y) + sin(x − y)]/2
- cosx⋅cosy = [cos(x + y) + cos(x − y)]/2
- sinx⋅siny = [cos(x − y) − cos(x + y)]/2
List of Trigonometry Formulas
The table given below consists of basic trigonometry ratios for angles such as such as 0°, 30°, 45°, 60°, and 90° that are commonly used for solving problems.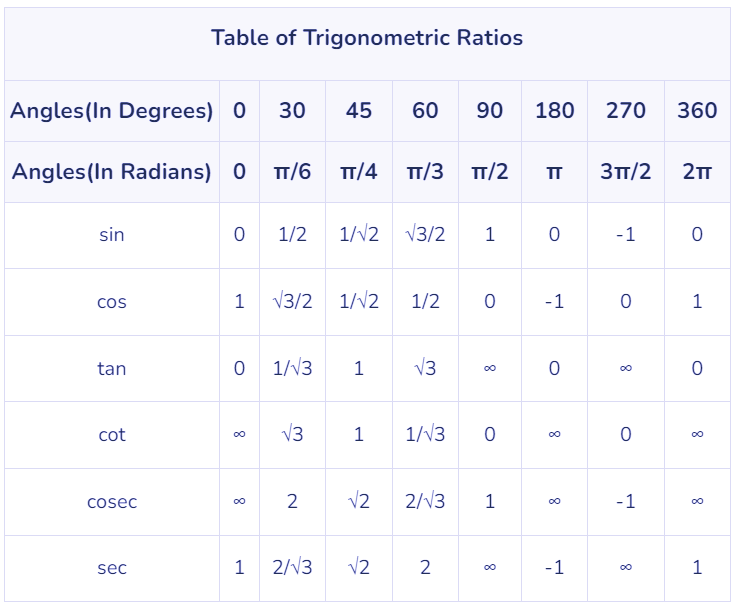
Solved Questions on Trigonometry Formula
Here are some solved examples of trigonometry formulas to help you get a better grasp of the concepts.
Que1: If cosec θ + cot θ = x, find the value of cosec θ – cot θ using trigonometry formula.
Sol: cosec θ + cot θ = x
We know that cosec2θ+ cot2θ = 1
(cosec θ -cot θ)( cosec θ+ cot θ) = 1
(cosec θ -cot θ) x = 1
cosec θ -cot θ = 1/x
Que2: With the help of trigonometric formulas, prove that (tan θ + sec θ – 1)/(tan θ – sec θ + 1) = (1 + sin θ)/cos θ.
Sol: L.H.S = (tan θ + sec θ – 1)/(tan θ – sec θ + 1)
= [(tan θ + sec θ) – (sec2θ – tan2θ)]/(tan θ – sec θ + 1), [Since, sec2θ – tan2θ = 1]
= {(tan θ + sec θ) – (sec θ + tan θ) (sec θ – tan θ)}/(tan θ – sec θ + 1)
= {(tan θ + sec θ) (1 – sec θ + tan θ)}/(tan θ – sec θ + 1)
= {(tan θ + sec θ) (tan θ – sec θ + 1)}/(tan θ – sec θ + 1)
= tan θ + sec θ
= (sin θ/cos θ) + (1/cos θ)
= (sin θ + 1)/cos θ
= (1 + sin θ)/cos θ = R.H.S. Proved.
Queue 3: If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of a+b/c+d
(a) 4
(b) 3
(c) 6
(d) 1
Sol: Start with the first equation:
cos A + cos² A = 1
Rearrange this equation:
cos² A = 1 - cos A
Now, since cos² A = 1 - sin² A, we can replace cos² A in the equation:
1 - sin² A = 1 - cos A
This simplifies to:
sin² A = cos A
Thus, we have the relationship between sin² A and cos A
The second equation is:
a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0
From the first equation, we know sin² A = cos A, so let's substitute sin² A with cos A into the second equation.
Since this is a polynomial expression in sin terms, solving it directly may require specific values for A (like 0, π/2, etc.).
By trial and error, considering the form of the equations, we find that the correct value of (a + b) / (c + d) is 4.
|
167 videos|238 docs|95 tests
|
FAQs on Important Formulas: Trigonometry - Quantitative Aptitude (Quant) - CAT
| 1. What are the basic trigonometric ratios? |  |
| 2. What are some common trigonometric identities? |  |
| 3. What are some important formulas in trigonometry? |  |
| 4. How do trigonometry functions help in real-life applications? |  |
| 5. How can I remember all the trigonometric formulas and identities? |  |

















