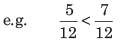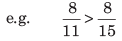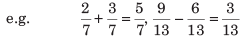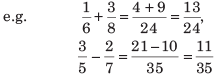Overview: Fractions | CSAT Preparation - UPSC PDF Download
| Table of contents |

|
| Importance in CSAT |

|
| Fraction |

|
| Comparison of Fractions |

|
| Operations on Fractions |

|
| Decimal Fractions |

|
Importance in CSAT
Most of the times direct questions are not asked from this chapter in CSAT exam, but its concepts are used with other topics like Percentage, Average, Elementary Algebra and various others.
In the years 2023-2018, questions are asked based on the various concepts like decimal fractions etc. that are used in this chapter
Therefore, a student has to be clarify all the concepts of this chapter.
A Fraction is a part of the whole thing whether it is an object, thing or region. It forms the part of basic aptitude of a person to have an idea, of the parts of a population, group or territory.
Fraction
All rational numbers which are of the form p/q ,where p, q are integers and p is not multiple of q , are known as a fractions. Here, p is called numerator whereas q is called denominator. e.g. To indicate that you have half a stick, it can be said that if you divide a stick into two equal parts, then you will have one part. This means you have 1 out of 2 parts of a stick. The part with you can be indicated as 1/ 2 . This is known as a fraction.
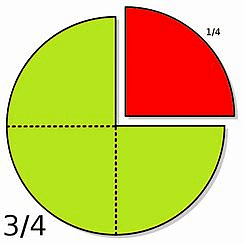
Types of Fractions
1. Proper fractions A fraction whose absolute value is less than 1, (i.e. their numerator is less than the denominator) is called a proper fraction.
2. Improper fractions When denominator is less than the numerator, then fraction is called improper fraction.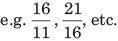
3. Complex fractions In such fractions, numerator or denominator or both are fractions.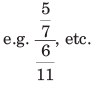
4. Compound fractions It is the fraction of fractions.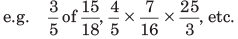
5. Inverse fractions It is the inverse of given fraction. e.g. Given fraction = 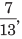 then inverse fraction =
then inverse fraction =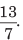
6. Mixed fractions If fractions having a whole number and proper fractions combined together are called mixed fractions.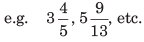
7. Continued fractions It contains an additional fractional part in numerator or denominator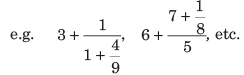
To simplify a continued fractions when the additional fractions part is in denominator, then start from bottom and solve upwards.
Comparison of Fractions
Two or more fractions can be compared with the help of the following rules:
- RULE 1: When two fractions have the same denominator, then greater fraction is that which has the greater numerator.

- RULE 2: When two fractions have same numerator, then greater fraction is that which has smaller denominator.

- RULE 3: When two or more fractions with different denominators and different numerators are to be compared, then following simple technique is used as discussed by the following steps :
- Step 1: Let the maximum number of digits in numerator be x and the maximum number of digits in denominator be y.
- Step 2: Find ( y − x ). If ( y − x ) = 0 or 1, multiply each fraction by 10 and if ( y − x ) = 2, 3, 4, then multiply each fraction by 102 103 104 , , , respectively.
- Step 3: After multiplication, find only the integer value of the resultant fraction. If from above step, any two fractions have the same integer value, then find the next decimal place and so on.
- Step 4: Compare the integer/decimal values obtained in above two steps. The fraction having maximum value is the greatest. e.g. Which is the greatest fraction?
e.g. Which is the greatest fraction?
Here, x = 3 (113, 303 and 144)
and y = 3 (173, 486 and 231)
∴ ( y − x ) = 0
So, on multiplying each fraction by 10, we get
Then, find integer values and if integer values are same, then proceed further to get the highest value after comparing the decimal values which is equal to 6.11, 6.53, 6.234, 6.233.
∴ Highest fraction or greatest fraction = 113/173
Lowest Term of a Fraction
Dividing the numerator and denominator by the HCF in them, we get the fraction in its lowest form. e.g. To find the fraction 6 / 14 in lowest form. Since, 2 is HCF in numerator (6) and denominator (14), so dividing both of them by 2, we get 3/7 which is the lowest form of 6/14.
Equivalent Fractions
If numerator and denominator of any fraction are multiplied by the same number, then all resulting fractions are called equivalent fractions.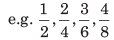 all are equivalent fractions but 1/2 is the lowest form.
all are equivalent fractions but 1/2 is the lowest form.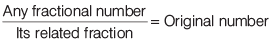
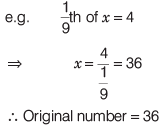
Operations on Fractions
Operations on fractions can be classified as 1. Addition and subtraction of fractions Here, two cases arise as denominators of the fractions are same or not.
- Case 1: When denominators of the two fractions are the same, we write denominator once and add (or subtract) the numerators.

- Case 2: If denominators are different, we need to find a common denominator that both denominators will divide into i.e. we need to take the LCM of denominators.

Illustration: 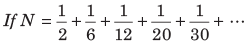

(a) 12/13
(b) 13/12
(c) 1/13
(d) 1
Sol: We have, 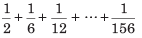
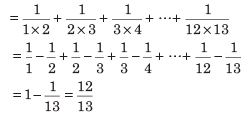
Decimal Fractions
The fractions in which denominators has the power of 10 are called decimal fractions. e.g. 0.25 = Zero point two five = 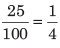
One-quarter 0.1 = Zero point one = 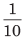 = One-tenth
= One-tenth
In 13.489, 13 is an integral part while 0.489 is the decimal part.
To Reduce any Decimal to a Fraction
To convert a decimal fraction follow the rules given below:
(i) Place 1 is the denominator under the decimal point of the given number.
(ii) After removing the decimal point, place as many zeroes after it as the number of digits after the decimal point.
(iii) Finally, reduce the fraction into its lowest form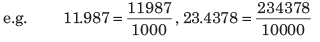
Operations on Decimal Fractions
Operations on decimal fractions can be classified as 1. Addition or subtraction of decimal fractions In the addition or subtraction of decimal fractions, we write the decimal fractions in such a way that all the decimal points are in the same straight line, then these numbers can be added or subtracted in a simple manner.
Illustration: If share of Karan, Raja, Darmesh in a sum of 1 is 0.68, 0.062 and 0.20, respectively and the rest of the share belongs of Deepak, then share of Deepak is given as
(a) 0.058
(b) 0.048
(c) 0.942
(d) 0.0942
Sol: (a) Let the share of Deepak be x.
Then, sum of shares of Deepak, Karan, Raja and Darmesh = 1
⇒ x + 0.68 + 0.062 + 0.20 = 1 ⇒ x + 0.942 = 1
∴ x = 1 − 0.942 = 0.058
Hence, share of Deepak is given as 0.058.
2. Multiplication of decimal fractions To multiply by powers of 10, the decimal point is moved to the right by as many places as there are number of zero/zeroes in the power of 10.
e.g. 0.75 × 10 = ?, 0.75 × 10 = 7.5
(the decimal point is shifted to right by one place)
To multiply decimals by number other than 10, we ignore the decimal point and multiply them in simple manner and atlast, put the points after the number of digits (from right) corresponding to the given problem.
Terminating and Non-terminating Recurring Decimals Fractions
If decimal expression of any fraction is terminated, then fraction is called terminating.
As, 
But, if we take example 33 ÷ 26, then
In this division, we see that remainder at the stages A and B are same.
In the continued process of division by 26, the digits 6, 9, 2, 3, 0, 7 in the quotient will repeat onwards.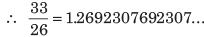
This process of division is non-terminating.
Therefore, such decimal expressions are called non-terminating recurring (repeating) decimals. On repeating digits, we put
Non-terminating, Non-recurring Decimals Fractions
Every fraction can be put in the form of terminating or non-terminating recurring decimals i.e. these decimal numbers can be put in the form of p / q. These are called rational numbers but some decimals numbers that cannot be put in the form of p / q, these are non-terminating, non-recurring decimals.
Also, these are called irrational numbers.
e.g. 0.101001000100001…
Method to Convert Non-terminating Recurring Decimals into Simple Fractions
First, write the non-terminating recurring decimal in bar notation. Then, write the digit in the denominators as many nines as number of digits recurring in the numerator. Also, don’t put decimal in the numerator.
Illustration: Convert 0.33333... into simple fraction.
(a) 3/10
(b) 1/3
(c) 33/100
(d) 11/32
Sol: (b) 0.3333… can be written as 0.3.
Now, to convert it into simple fraction, we will put as many 9 in denominator as in decimal.
∴ 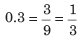
Mixed Recurring Decimals Fractions
A decimal fraction in which some digits are not repeated and some are repeated are called mixed recurring decimals fractions. e.g. 1.171734561818
Method to Convert Mixed Recurring Decimal Fraction into Simple Fraction
First, we subtract non-repeated part from the number (without decimal) and put number nines as many times as number of recurring digits and also put the number 0 as many times odd number of non-recurring digits.
Illustration: Convert 3.0072 into the simple fraction.
(a) 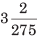
(b) 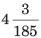
(c) 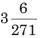
(d)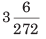
Sol: 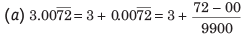
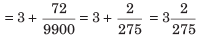
|
210 videos|138 docs|138 tests
|
FAQs on Overview: Fractions - CSAT Preparation - UPSC
| 1. How are fractions important in the CSAT exam? |  |
| 2. How can fractions be compared in the CSAT exam? |  |
| 3. What are the basic operations on fractions tested in the CSAT exam? |  |
| 4. How are decimal fractions relevant in the CSAT exam? |  |
| 5. How can candidates prepare effectively for fractions in the CSAT exam? |  |

|
Explore Courses for UPSC exam
|

|