Thermal Expansion | Physics for JEE Main & Advanced PDF Download
| Table of contents |

|
| What is Thermal Expansion? |

|
| Types of Expansion |

|
| Water's Unique Behavior |

|
| Practical Applications of Expansion |

|
| Solved Examples |

|
What is Thermal Expansion?
- When a liquid is heated, such as when a thermometer is placed in warm water, it expands. Conversely, it contracts when cooled.
- Similar to liquids, balloons demonstrate thermal expansion. A balloon inflated in a warm environment expands fully, while one in a cold environment shrinks when fully inflated due to air contraction.
- Sealed bottles with tightly screwed metallic lids may require dipping in hot water to loosen the lid, as the expansion of the metallic lid facilitates easier opening.
Most substances expand with heat and contract with cold. This change in dimensions with temperature variation is known as thermal expansion.
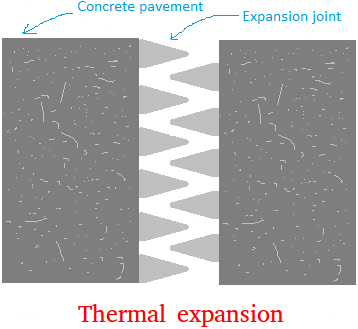 Example of Thermal Expansion
Example of Thermal Expansion
Types of Expansion
There are 3 types of expansion which occur in solids-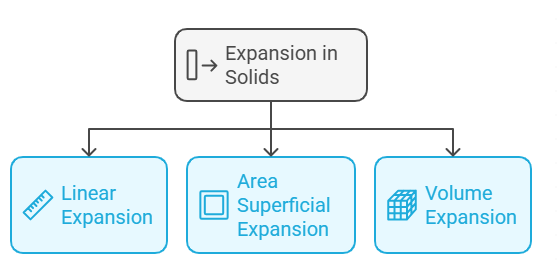
1. Linear Expansion
- Linear Expansion refers to the increase in length of a solid object when its temperature increases while keeping pressure constant.
- Linear expansion is expressed by the formula:
Here, αl represents the coefficient of linear expansion for the specific solid. - The unit of α is per degree Celsius (°C-1) in the CGS system and per Kelvin (K-1) in the SI system.
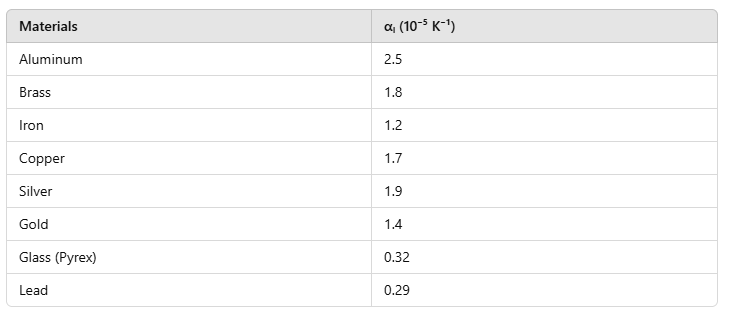
- The coefficient of linear expansion for some materials is as follows:
2. Area Superficial Expansion
- It involves the increase in the surface area of a substance when heated. A slight change in temperature, ΔT, leads to deformation, where the fractional change in surface area, ΔA/A, is directly proportional to ΔT.
- The formula for Area expansion is:
Here, αA represents the coefficient of area expansion of the given solid.
3. Volume Expansion
- It refers to the fractional change in the volume of a substance. A slight variation in temperature, ΔT, causes deformation, where the fractional change in volume, ΔV/V, is directly proportional to ΔT.
- The formula for volume expansion is:
Here, αV is another characteristic of the substance, but it varies with temperature.
- The coefficient of volume expansion only becomes constant at high temperatures.
- For instance, ethyl alcohol has a higher coefficient of volume expansion than mercury and thus expands more for the same temperature rise.
The graph depicts the Coefficient of volume expansion of copper concerning temperature:
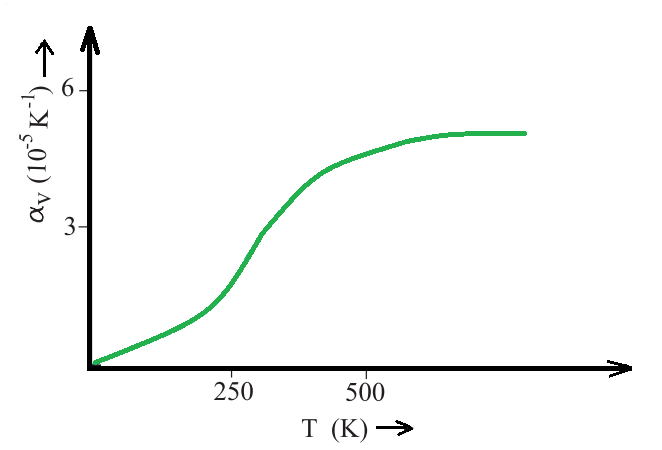 It shows how the Coefficient of volume expansion of copper changes with temperature.
It shows how the Coefficient of volume expansion of copper changes with temperature.
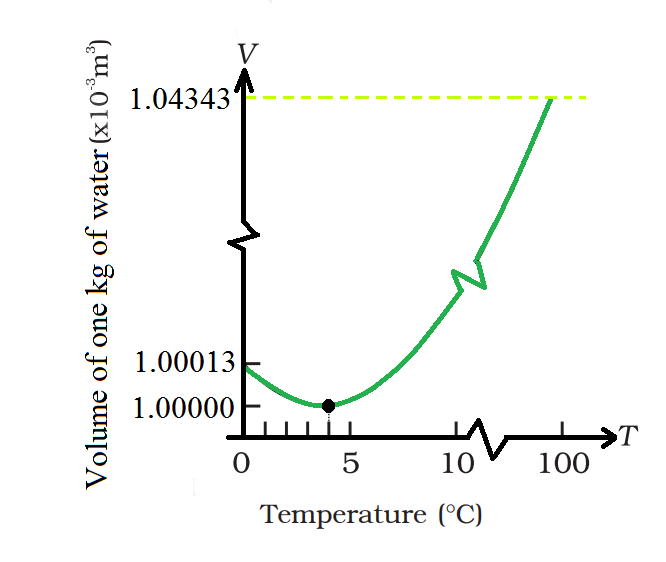
Water's Unique Behavior
- 0 to 4 Degrees Celsius: Water behaves unusually when heated in this range.
- Cooling to 4°C: Water's volume decreases as it cools to this temperature.
- Below 4°C: Water's volume increases, leading to a decrease in density. This is unusual because most substances contract when cooled.
- Maximum Density: Water reaches its maximum density at 4°C, which impacts how lakes and ponds freeze.
- Energy Loss Process: This process allows denser water to sink while warmer water rises, creating movement in the water.
- Freezing Process: When the cooler water on the surface drops below 4°C, it becomes less dense and freezes on top.
Practical Applications of Expansion
- Space is left between the ends of two rails when rails are laid down on the ground.
- The transmission cables are loosely attached to the poles.
- The iron rim that goes on a cart wheel is always slightly smaller in diameter than the wheel itself.
- A glass stopper stuck in the neck of a glass bottle can be removed by warming the bottle’s neck.
Young's Modulus and Stress-Strain Relationship
- Young's modulus is a constant that applies to a specific material.
- Wire 1 has a cross-sectional area denoted as A, while wire 2 has a cross-sectional area of 3A.
- The volumes of wire 1 and wire 2 are equal, represented by the equation V1 = V2.
- From the relationship A × l1 = 3A × l2, we can deduce that l2 = l1/3.
- The stress-strain relationship is expressed as Y = (F/A)/(Δl/l), where F1 = YA(Δl1/l1) and F2 = Y3A(Δl2/l2).
- It is crucial to understand that elongation may differ based on the individual properties and loads of the wires.
- By substituting the appropriate values, we can determine that F2 = 9F1.
Relationship between Area Expansion and Coefficients
- Area Expansion refers to the increase in the surface area of a substance when it is heated, resulting in a rise in temperature. The fractional change in surface area, represented as ΔA/A, is directly related to the change in temperature, ΔT.
- The relationship can be expressed mathematically as ΔA/A = αA × ΔT, where αA is the coefficient of area expansion.
- Derivation of Coefficients: The relationship between the coefficient of area expansion (αA) and the coefficient of linear expansion (αl) can be derived as αA = 2αl. This indicates that the coefficient of area expansion is twice that of linear expansion.
- Uniform Expansion of a Cube: Consider a cube that expands uniformly in all directions with an increase in temperature. The new area after expansion is connected to the linear expansion of the cube.
- The equation ΔA/A = 2(Δl/l) leads to the derivation of αA = 2αl, reinforcing the idea that the coefficient of area expansion is double that of linear expansion.
Solved Examples
Example 1: A steel tape 1 m long is correctly calibrated for a temperature of 27°C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0°C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27°C? Coefficient of linear expansion of steel = 1.20 × 10⁻⁶ °C⁻¹?
Sol: Length of rod at 45.0°C = 63 cm
t₁ = 27.0°C, t₂ = 45.0°C, α = 1.20 × 10⁻⁶ °C⁻¹
Length of steel rod at 45°C is given by
L₂ = L₁ [1 + α(t₂ - t₁)]
= 63 [1 + 1.2 × 10⁻⁶ × (45 - 27)]
= 63 [1 + 1.2 × 10⁻⁶ × 18]
= 63.0136 cm
The change in length = 63.0136 - 63 = 0.0136 cm.
As the data is correct up to three significant figures, hence the actual length of rod at 27°C as measured by tape = 63.0 cm.
Example 2: A brass wire 1.8 m long at 27°C is held taut with little tension between two rigid supports. If the wire is cooled to a temperature of -39°C, what is the tension developed in the wire, if its diameter is 2.0 m? Coefficient of linear expansion of brass = 2.0 × 10⁻⁵ °C⁻¹; Young’s modulus of brass = 0.91 × 10¹¹ Pa.
Solution:When the wire is cooled from 27°C to -39°C, the change in temperature Δt = 27 - (-39) = 66°C. The corresponding decrease in length Δl = αlΔt.
This will produce the contraction strain in the wire given by:
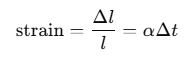
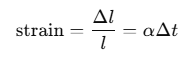
Thus, the stress produced = Y × strain = Y × α × Δt.
Now the force or tension in the wire = stress × area of cross-section
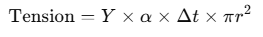
Substitute the values:
=
So, the tension developed in the wire is approximately 370 N.
Example 3: Determine the pressure needed to maintain the original length of a steel wire when its temperature is increased by 100°C. Given: ΔT = 100°C, Y = 2 x 1011 Nm−2 , α = 1.1 x 10−5 K−1 .
Sol: Given:
- α = 1.1 x 10−5 K−1
- ΔT = 100°C = 100 K (since the change in temperature is the same in Celsius and Kelvin)
Thermal Strain (ε) = αΔT
ε = (1.1 x 10−5 K−1 ) × (100 K)
ε = 1.1 x 10−3
The thermal strain represents the fractional change in length due to the temperature increase. To maintain the original length of the wire, this strain must be countered by an applied stress (σ).
σ = Y × ε
⇒ F = σ × A
Where: A = Cross-sectional area of the wire
Substituting the values:
F = (Y × ε) × A
F = (2 x 1011 Nm−2 ) × (1.1 x 10−3 ) × A
F = 2.2 x 108 N/m2 × A
|
268 videos|740 docs|171 tests
|
FAQs on Thermal Expansion - Physics for JEE Main & Advanced
| 1. What is thermal expansion and how does it occur? |  |
| 2. What are the different types of thermal expansion? |  |
| 3. Why is water's behavior during thermal expansion unique? |  |
| 4. What are some practical applications of thermal expansion? |  |
| 5. Can thermal expansion lead to any problems in engineering or construction? |  |















