Fair Share Chapter Notes | Mathematics for Class 3 (Maths Mela) PDF Download
| Table of contents |

|
| Introduction |

|
| Sharing Things Equally |

|
| Understanding Halves and Doubles |

|
| Learn with Stories |

|
| Understanding Halves and Quarters |

|
| Understanding Quarters and Wholes |

|
| Let's Practice |

|
Introduction
Imagine you have a yummy chocolate bar, and you want to share it with your friend. But wait! How do you make sure you both get an equal piece? That's what we'll learn in our exciting chapter on "Fair Share." We'll explore fun ways to divide treats like chocolates and parathas equally, making sharing fair and enjoyable for everyone. 
Sharing Things Equally
Imagine your summer vacations are going on and your best friend came to your house for a visit. Your mom prepared you a pizza and asked to share the yummy pizza with your friend. But how would you do so?
Yes, you guessed right! You'll cut the pizza in a way that you and your friend get equal share of the pizza.
- When you cut the pizza right down the middle, you make two parts that are exactly the same size.
- Each of these parts is called a "half" because it's one of the two equal pieces.

- Now, if you take one of these halves, you have half of the pizza. But what about the other half? It's still there, right? That's what we call the "full" pizza.
- When you put both halves together, you have the full pizza again!
So, what do we learnt from here? When 1 whole is shared equally between 2 people, each share is called a half!
That's how we understand the concepts of half and full—dividing things equally and knowing how the parts fit together to make the whole.
Let's Practice!
1. You've been given some shapes and you're required to divide each shape into two equal halves using a line.
After dividing the shapes into equal halves, they would look something like : 2. You've been given some shapes with some of their part shaded. You're identify which one is equally shared and circle them.
2. You've been given some shapes with some of their part shaded. You're identify which one is equally shared and circle them.
The circled shapes below are the ones which are equally shared (equally halved):

Here, we haven't circled the pizza and the paratha because:
- Pizza is not equally halved, but contains more than half of the whole.
- Paratha is not exactly halved, one half is bigger than the other half.
Great job! Now you know how to share things fairly and understand what halves are all about. You also learned how to tell when exactly half of something is shaded.
Understanding Halves and Doubles
Imagine you and your friend have some marbles. You count them and find that you have 3 marbles, while your friend has 6. That’s a lot more!
Now, let's see what's happening here.
- When you have 3 marbles and your friend has 6, you can say that your 3 marbles are half of your friend's 6 marbles.
- It's like saying your friend has double the number of chocolates you have—twice as much!
Understanding halves and doubles helps us compare quantities. It shows how things can be divided equally or doubled up.
Learn with Stories
Once upon a time, there were two best friends named Mia and Leo. They loved spending time together, especially when it involved yummy treats. One sunny afternoon, Mia's mom baked a delicious round cake for them to share.
- Mia and Leo sat down at the table, excited to enjoy the cake. Mia said, "Let's cut the cake into halves so we both get an equal piece."
- Leo asked, "What does cutting the cake into halves mean?"
- Mia smiled and explained, "Cutting the cake into halves means we divide it into two equal parts. It’s like drawing a line down the middle so we each get the same amount."

- Mia carefully took a knife and cut the cake straight down the middle, creating two equal halves. Each half looked exactly the same, and Mia and Leo each got one half of the cake.
- Later, Mia's mom brought out another cake, but this time it was a rectangular cake. Leo said, "Let's try doubling this cake!"
- Mia was curious and asked, "What do you mean by doubling the cake?"
- Leo explained, "Doubling the cake means we take what we have and make it twice as big. If we have one cake, doubling it would give us two cakes."
- Mia and Leo pretended they had another identical rectangular cake. They placed the two cakes side by side and noticed that the area covered by both cakes together was double the area of one cake.

- Leo said, "So, halving means cutting something into two equal parts, like when we split the round cake into halves. And doubling means making it twice as big, like imagining we have two rectangular cakes instead of one."
Mia and Leo enjoyed their cakes, feeling happy and full, and they both learned a fun and delicious lesson about halves and doubles.
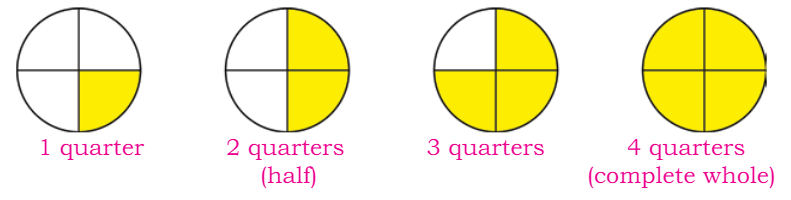
Understanding Halves and Quarters
Imagine you have big pile of oranges.
- A half means dividing them into two equal parts. It is written as 1/2.
So, if you have 8 oranges and want to find half of them, you just need to share them equally. That means each half will have 8/2 =4 oranges.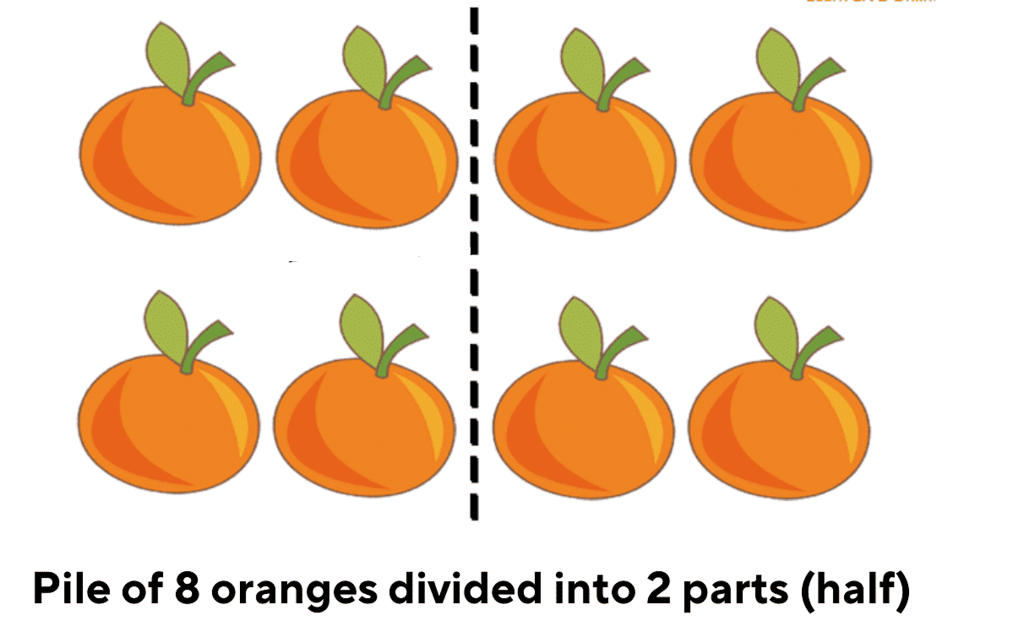 Now, let's say you need to share your oranges with a friend, and you have to give a quarter of them.
Now, let's say you need to share your oranges with a friend, and you have to give a quarter of them.
- A quarter means dividing them into four equal parts. It is written as 1/4.
So, if you have 8 oranges, you divide them into 4 equal parts. Each part will have 8/4 =2 oranges. So, when you give your friend a quarter of your oranges, you're giving them 2 oranges.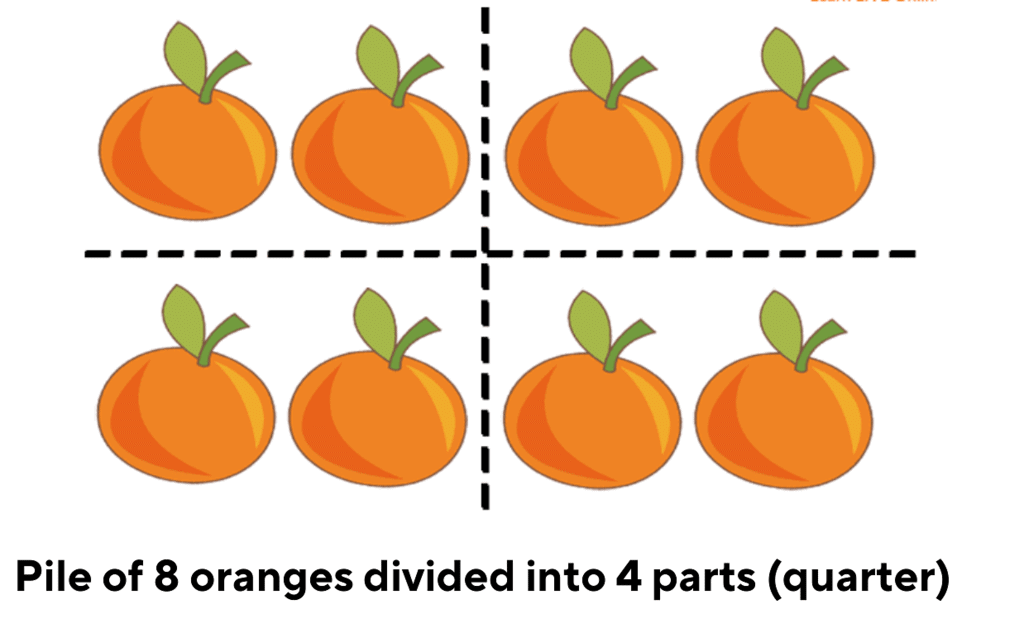 Understanding about halves and quarters helps us share things fairly and divide them equally. Whether it's sharing oranges or anything else, learning about halves and quarters makes numbers more fun to understand!
Understanding about halves and quarters helps us share things fairly and divide them equally. Whether it's sharing oranges or anything else, learning about halves and quarters makes numbers more fun to understand!
Understanding Quarters and Wholes
Imagine you have a delicious pizza.
As you've already understood about quarters,
- When we talk about quarters, we're talking about cutting that pizza into 4 equal parts, just like four slices.
Each slice is called a quarter. So, if you cut your pizza into four slices, each slice is one quarter of the whole pizza.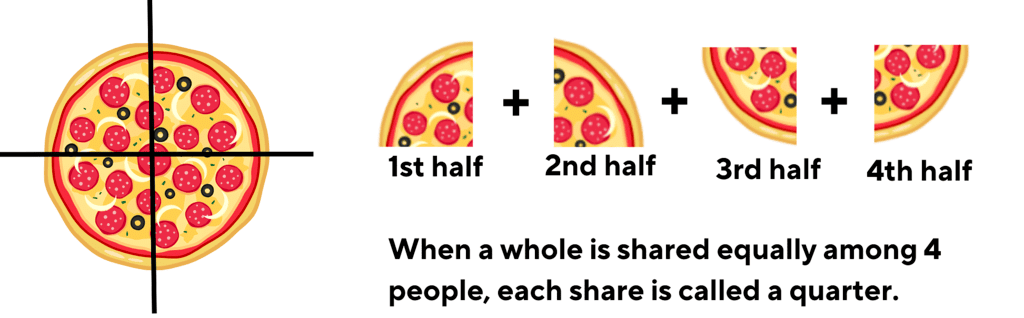 Now, when we say "wholes," we mean the complete pizza i.e. 4 slices put together. So, if you have all four quarters of the pizza, you have the complete pizza—a whole pizza!
Now, when we say "wholes," we mean the complete pizza i.e. 4 slices put together. So, if you have all four quarters of the pizza, you have the complete pizza—a whole pizza!
And mathematically, we can say that:
1 quarter + 1 quarter + 1 quarter + 1 quarter = 4 quarters = 1 whole
So, 4 quarters make a whole pizza!
Edurev Tip:
Let's Practice
Question: Use the clues to find the correct option. Also, Tick the correct option:
"I have less than double of 3 marbles.
I have more than half of 8 marbles."

 View Answer
View Answer 
Answer:
 (i) Double of 3 marbles = 3 x 2 = 6 marbles.
(i) Double of 3 marbles = 3 x 2 = 6 marbles.
Less than double of 3 marbles means less than 6 marbles.
(ii) Half of 8 marbles = 8/2 = 4 marbles.
More than half of 8 marbles means more than 4 marbles.
Hence, the correct option is (b) 5 marbles because it is less than 6 marbles and more than 4 marbles.
Question: You've been given some shapes and you're required to make a quarter of a whole using a line.
 View Answer
View Answer 
Answer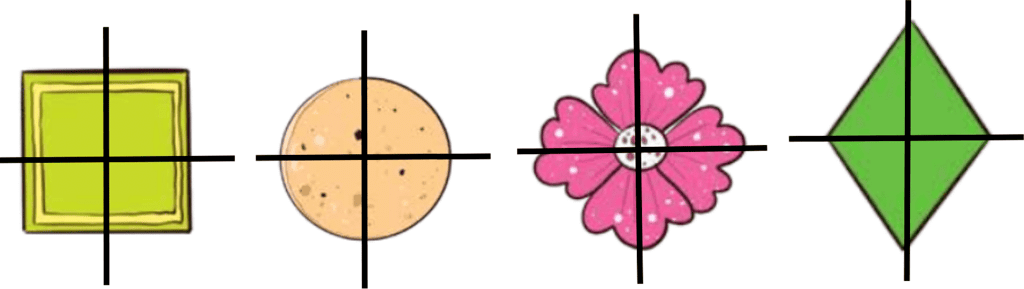
Question: You've been given some shapes and you're required to tick mark the shapes which show three-quarters.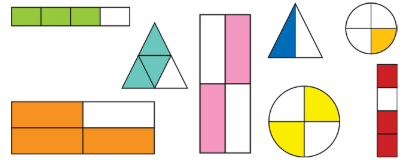
 View Answer
View Answer 
Answer: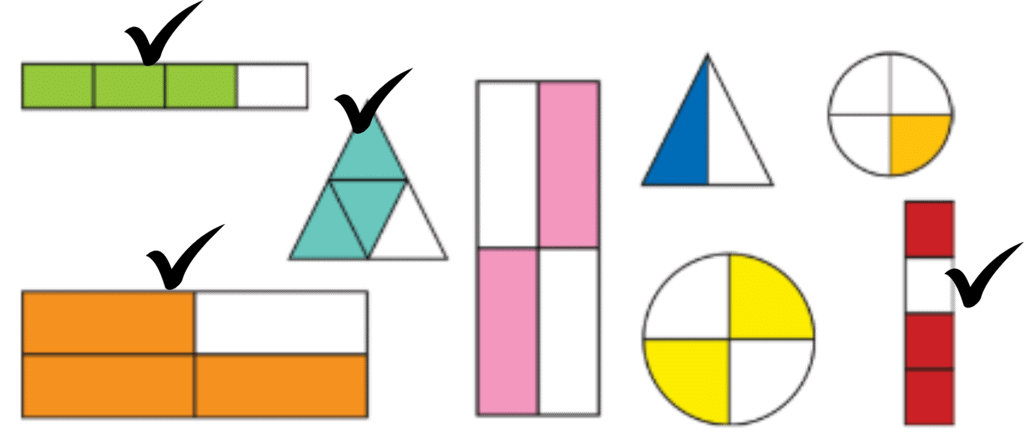
Question: Show quarters and halves in different ways in the grids given below. 
 View Answer
View Answer 
Answer: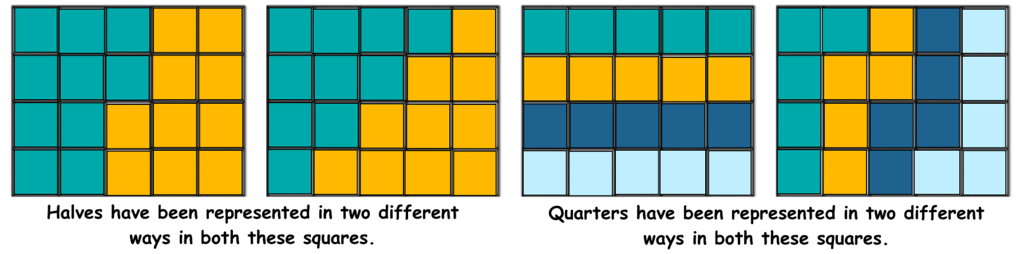
- In first two squares, two different patterns have been shown to divide a square into equal halves.
- In last two squares, two different patterns have been shown to divide a square into quarters.
|
26 videos|180 docs|28 tests
|
FAQs on Fair Share Chapter Notes - Mathematics for Class 3 (Maths Mela)
| 1. What are halves and how can we identify them in everyday situations? |  |
| 2. How can I explain the concept of quarters to my child? |  |
| 3. What is the difference between doubles and halves? |  |
| 4. How can stories help in understanding fractions like halves and quarters? |  |
| 5. What are some practical exercises to practice understanding fractions? |  |