Year 7 Exam > Year 7 Notes > Roots
Roots - Year 7 PDF Download
Introduction
- Square Numbers: These are the results obtained when a number is multiplied by itself. For instance, 4 multiplied by 4 equals 16.
- Cube Numbers: A cube number results from multiplying a number by itself three times. An example is 3 cubed, which equals 27.
- Powers and Indices: Powers are represented by small digits called indices. For example, 3 to the power of 2 is written as 32.
- Square Roots: The opposite operation of squaring a number is finding the square root. It may not always yield an integer, in which case a calculator's square root (√) function is used, usually rounded to one decimal place.
- Cube Roots: The inverse process of cubing a number is determining the cube root. This is essential to find the original number when it has been cubed.
Finding the square root
- Squaring a number involves multiplying a number by itself. For instance, 42 is equivalent to 4 x 4.
- The opposite operation of squaring a number is known as finding the square root. The square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 36 is 6 since 62 equals 36. Additionally, -6 is also a square root of 36, as (-6)2 equals 36.
- When determining the square root of a number, there are two solutions: a positive and a negative root. These roots can be expressed individually or with the ± symbol. For instance, the square root of 16 yields two results: 4 and -4, which can be written as ±4.
- The symbol for denoting the square root is √. For example, √36 represents "the square root of 36," which equals 6. It's beneficial to memorize the first 12 square numbers: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, and 144.
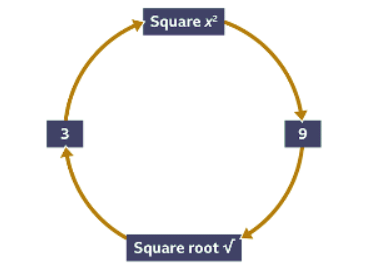
- This image shows the link between squaring and finding the square root of a number. 3 squared is 9 (because 32 = 3 x 3 = 9). The opposite of squaring a number is called finding the square root. The square root of 9 is 3
Examples
Example 1: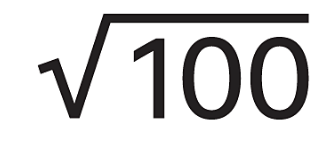
- √100 means ‘the square root of 100’. Find the square root of 100
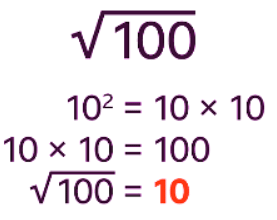
- Find the square root of 100. 102 means 10 x 10. This equals 100. The square root of 100 is 10
Example 2:
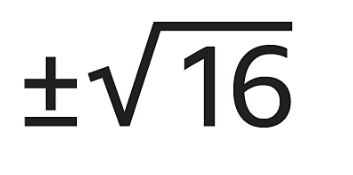
- Find both roots of 16 (a positive and negative solution).
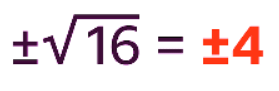
- The square root of 16 is 4 (because 42 = 4 x 4 = 16). The square root of 16 is also -4 (because -42 = -4 x -4 = +16). This is usually written as ±4
Finding the Cube Root
- A cube number is a number that is the result of multiplying a number by itself three times. For instance, 4³ equals 4 x 4 x 4.
- The opposite operation of cubing a number is known as finding the cube root. This process is represented by the symbol "³√". It's important to note that the cube root of a number may not always be a whole number. In such cases, you can use the "³√" function on a calculator and round the result to one decimal place.
- Memorizing the initial cube numbers like 1, 8, 27, 64, 125, and 216 can be beneficial in mathematical computations.

- This image illustrates the relationship between cubing and finding the cube root of a number. For instance, 4 cubed equals 64 (43 = 4 x 4 x 4 = 64). Finding the cube root of 64 results in 4.
Examples
Example 1:
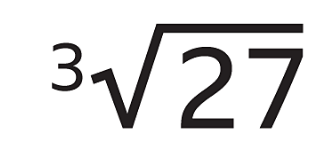
- ³√27 means ‘the cube root of 27’. Find the cube root of 27
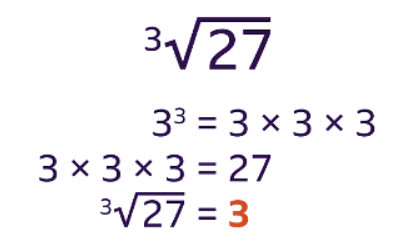
- 33 = 3 x 3 x 3 which equals 27. The cube root of 27 is 3
Example 2:
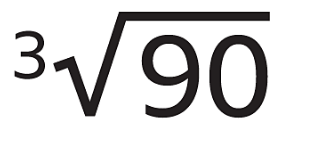
- Find the cube root of 90. 90 is not a cube number. The cube root of 90 therefore is not a whole number.
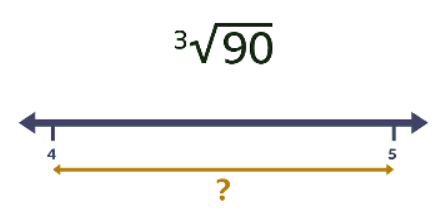
- 43 = 64 and 53 = 125. Therefore ³√90 lies between 4 and 5. Use the ³√ button on a calculator to find the exact value.
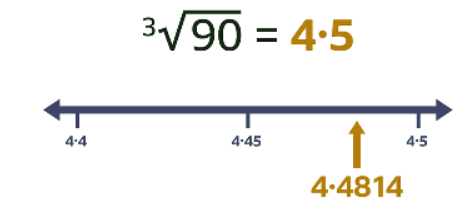
- ³√90 = 4∙4814... Round this answer to 1 decimal place. A number line can help when rounding. 4∙4814 rounded to 1 decimal place is 4∙5. ³√90 = 4∙5 (to 1 decimal place).
Question for RootsTry yourself: What is the result of 5 squared?View Solution
FAQs on Roots - Year 7
| 1. How do you find the square root of a number? |  |
Ans. To find the square root of a number, you can use methods such as prime factorization, long division, or a calculator. For example, to find the square root of 144, you would take the square root of 12 since 12 x 12 = 144.
| 2. What is the process for finding the cube root of a number? |  |
Ans. To find the cube root of a number, you can use methods similar to finding the square root, but instead, you are looking for the number that, when multiplied by itself three times, equals the original number. For example, the cube root of 27 is 3 since 3 x 3 x 3 = 27.
| 3. Can you find the square root of a negative number? |  |
Ans. Yes, you can find the square root of a negative number, but the result is a complex number. For example, the square root of -16 is 4i, where "i" represents the imaginary unit.
| 4. Is it possible to find the cube root of a negative number? |  |
Ans. Yes, it is possible to find the cube root of a negative number. Similar to finding the square root of a negative number, the result will be a complex number. For example, the cube root of -64 is -4, since -4 x -4 x -4 = -64.
| 5. How can you use the square root and cube root in real-life situations? |  |
Ans. Square roots and cube roots are often used in various real-life situations, such as calculating areas of squares and cubes, determining dimensions of objects, and solving mathematical problems in fields like engineering, physics, and finance.
Related Searches


















