What is a Common Factor? - Year 7 PDF Download
| Table of contents |

|
| Introduction |

|
| How to find common factors |

|
| Find the HCF of two or more numbers |

|
| Find the LCM of two or more numbers |

|
| How to use a Venn diagram to find the HCF and LCM |

|
| Real-world maths |

|
Introduction
- A common factor is a whole number that is a factor of two or more numbers. For example, 2, 5, and 10 are common factors of 30. A whole number that divides into another number with no remainder.
- The highest common factor (HCF) is the largest factor that divides into the selected numbers. For instance, 10 is the highest common factor of 30 and 20. It is denoted as HCF.
- The lowest common multiple (LCM) is the smallest multiple common to two or more numbers. An example is the LCM of 15 and 12, which is 60, the lowest common multiple in their multiplication tables.
- The HCF and LCM are essential when adding and subtracting fractions and can be determined by listing factors and multiples. For larger values, expressing numbers as a product of prime factors is more efficient.
- A Venn diagram is a simple visual representation with overlapping circles, used to illustrate relationships between different groups or sets.
How to find common factors
- A common factor is a whole number that is a factor of two or more numbers. For example, 2, 5, and 10 are common factors of 30 and 20. Note that 1 is a common factor of all whole numbers.
- To find common factors:
- List the factors of each number.
- Compare the factors to find numbers that are the same (or common) in each list.
Example
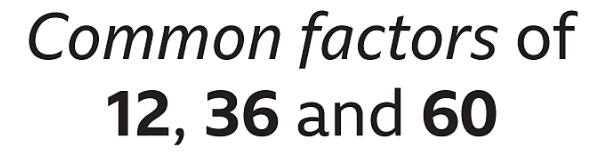
- Find the common factors of 12, 36 and 60

- List the factors of 12, the factors of 36 and the factors of 60
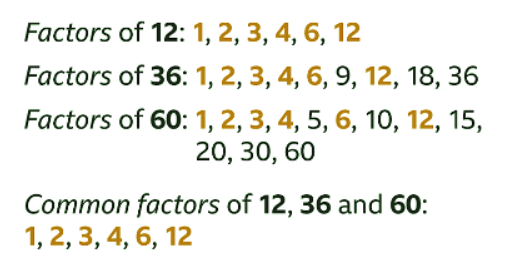
- Compare the lists of factors to find numbers that occur in all three lists. The common factors of 12, 36 and 60 are 1, 2, 3, 4, 6, and 12.12 is a factor of both 36 and 60, so all its factors will be common factors of 36 and 60
Find the HCF of two or more numbers
- The highest common factor (HCF) is the largest factor that divides into the selected numbers. For example, 10 is the HCF of 30 and 20. It's denoted as HCF.
- To determine the HCF of two or more numbers, you need to identify the greatest factor that they have in common.
- One method to find the HCF is by listing the factors of the numbers. For larger numbers, prime factorization can be used.
By listing
- List the factors of each number.
- Compare the lists to find the greatest number common to both.
By prime factorisation
- Draw factor trees for each number. You may need to review how to draw a factor tree.
- Write each number as a product of its prime factors. It can be easier to not use index form.
- Identify the common prime factors in each product of prime factors.
- To find the HCF, multiply the common prime factors.
Remember: Index form is an abbreviation for repeated multiplication. Eg, 52 means 5 × 5. 53 means 5 × 5 × 5
Example
Example: Find the HCF of 30 and 36
Sol: By listing
List the factors of 30 and the factors of 36. The highest factor that is common to both lists is the HCF of 30 and 36
Factors of 30: 1, 2, 3, 5, 6,10, 15, 30
Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
HCF of 30 and 36 = 6
By prime factorisation
Draw and complete a factor tree for 30 and a factor tree for 36
Use the factor trees to write 30 and 36 as a product of their prime factors.
30 = 2 × 3 × 5
36 = 2 × 2 × 3 × 3
The common prime factors are 2 and 3. Multiply the common prime factors to find the HCF. 2 × 3 = 6
HCF of 30 and 36 = 6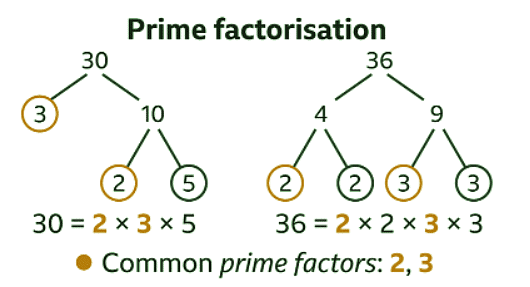
Find the LCM of two or more numbers
- Definition of a multiple: An integer that is in the multiplication table of a specific number. For example, 20 is a multiple of ten because 20 is in the ten times table.
- Definition of an integer: Any of the positive or negative whole numbers including zero.
- Definition of the lowest common multiple (LCM): The LCM is the lowest multiple that is common to two or more numbers. For instance, the LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. It is also known as the least common multiple.
By Listing
- List consecutive multiples for each number. These are essential for calculating the Least Common Multiple (LCM).
- The first multiple to occur in every list is the LCM. It helps in finding the common multiple efficiently.
By Prime Factorization
- Draw factor trees for each number.
- Write each number as a product of its prime factors . It can be easier to not use index form.
- Identify the common prime factors in each product of prime factor .
- The prime factors that are not common to each product are unique for that number.
- To find the LCM, multiply the common factors by the unique factors of one number and the unique factors of the other number.
Example
Example: Find the LCM of 30 and 36
Sol: By listing
List multiples of 30 and 36. The first multiple that occurs in both lists is the LCM.
Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240, 270, 300…
Multiples of 36: 36, 72, 108, 144, 180…
LCM of 30 and 36 is 180
By prime factorisation
Draw and complete a factor tree for 30 and a factor tree for 36
Use the factor trees to write 30 and 36 as a product of their prime factors
30 = 2 × 3 × 5
36 = 2 × 2 × 3 × 3
The common prime factors are 2 and 3. The unique prime factor of 30 is 5. The unique prime factors of 36 are 2 and 3
To find the LCM, multiply the common prime factors (2 and 3) by the unique prime factor of 30 (5) and the unique prime factors of 36 (2 and 3)2 × 3 × 5 × 2 × 3 = 180
LCM of 30 and 36 is 180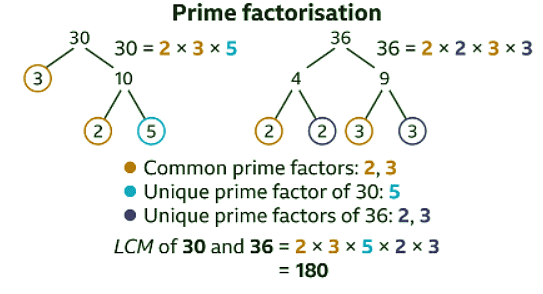
How to use a Venn diagram to find the HCF and LCM
To use a Venn diagram - a simple visual diagram with overlapping circles, used to show the relationships between two different groups or sets - to find the HCF and LCM of two numbers:
- Write each number as a product of prime factors
- Product of prime factors: The factors of 12 are 1, 2, 3, 4, 6, and 12. The prime factors of 12 are 2 and 3. 12 may be expressed as a product of its prime factors: 12 = 2 × 2 × 3
- Draw a Venn diagram:
- Draw a circle to represent each number being analyzed.
- Identify and list the factors that are common to both numbers in the area where the circles overlap.
- Allocate the remaining prime factors unique to the first number within its respective circle.
- Assign the remaining prime factors unique to the second number within its individual circle.
- Verify that each circle encapsulates the complete prime factorization of the corresponding number.
- When analyzing two numbers, draw a circle for each number to visually represent their factors.
- Identify and place the factors that are common to both numbers in the region where the circles intersect.
- Place the prime factors exclusive to the first number within its circle.
- Within the circle representing the second number, allocate its distinctive prime factors.
- Ensure that each circle displays the full prime factorization for the respective number.
Example
Example: Use the Venn diagram to find the HCF and LCM of 240 and 180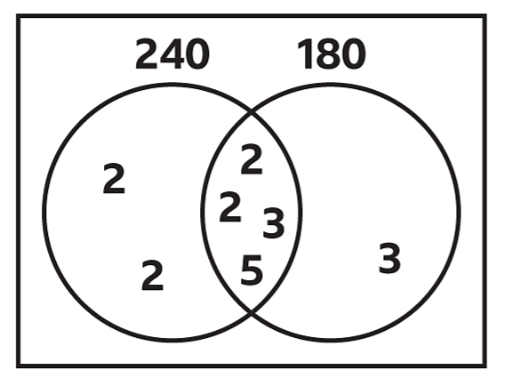 Sol: The product of prime factors in the intersection (the overlap) gives the HCF of 240 and 180
Sol: The product of prime factors in the intersection (the overlap) gives the HCF of 240 and 180
HCF of 240 and 180 = 2 × 2 × 3 × 5HCF = 60
The product of the prime factors in the circles gives the LCM of 240 and 180LCM of 240 and 180 = 2 × 2 × 3 × 5 × 2 × 2 × 3LCM = 720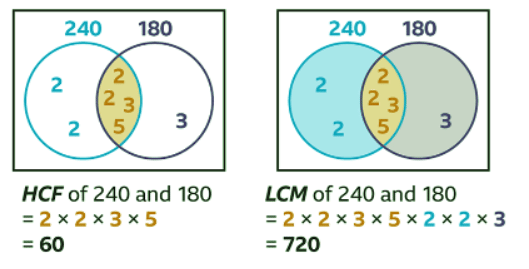
Real-world maths
The HCF and LCM can be useful for various businesses when ordering materials and stock.
- Calculating the HCF can help an independent stationery business use their materials efficiently. For example, card stock can be bought in lengths of 24 inches and 36 inches. The HCF of 24 and 36 is 12. By making cards sized 12 inches, they can minimize waste from card stock.
- Calculating the LCM can help an event planner manage their budget effectively. For instance, if stickers are sold in packs of 15 and tote bags are sold in packs of 6, they should buy these items in batches of 30. The LCM of 15 and 6 is 30. This means that purchasing 2 packs of stickers and 5 packs of tote bags gives 30 of each item, ensuring matching amounts for the gift bags.
FAQs on What is a Common Factor? - Year 7
| 1. What is a common factor and why is it important in mathematics? |  |
| 2. How can I find common factors of two or more numbers? |  |
| 3. What is the highest common factor (HCF) and how is it calculated? |  |
| 4. What is the lowest common multiple (LCM) and how is it calculated? |  |
| 5. How can I use a Venn diagram to find the HCF and LCM of numbers? |  |













