What is a Common Factor? - Year 7 PDF Download

Key points

• Common Factors

  A common factor is a whole number that divides evenly into two or more numbers without leaving a remainder. For example, 2, 5, and 10 are common factors of 30 and 20.

• Highest Common Factor (HCF)

  The highest common factor (HCF) is the largest factor that divides into two or more numbers. For instance, 10 is the HCF of 30 and 20. It is denoted as HCF.

• Lowest Common Multiple (LCM)

  The lowest common multiple (LCM) is the smallest multiple that is common to two or more numbers. For example, the LCM of 15 and 12 is 60. It is also known as the least common multiple.

• Using HCF and LCM

  HCF and LCM are essential when adding and subtracting fractions. They can be determined by listing factors and multiples. For larger numbers, expressing them as a product of prime factors is a more efficient method.

• Venn Diagrams

  A Venn diagram is a visual tool with overlapping circles used to illustrate relationships between different groups or sets.

Common Factors and Highest Common Factor (HCF)

Main Concepts:

• Common Factor:
  • Common factors are whole numbers that are factors of multiple numbers.
  • For instance, 2, 5, and 10 are common factors of both 30 and 20.
• Factor:
  • A factor divides into a number without leaving a remainder.
• Highest Common Factor (HCF):
  • The Highest Common Factor (HCF) is the largest factor that divides into the selected numbers completely.
  • For example, 10 is the HCF of 30 and 20.
  • HCF is denoted as the greatest factor that divides into two or more numbers.

Understanding Factors and Multiples

The concepts of factors and multiples are essential in mathematics, let's break them down for a clearer understanding:

Highest Common Factor (HCF)

• The Highest Common Factor (HCF) is the largest factor that divides into two or more numbers.
• For example, the HCF of 30 and 20 is 10 because 10 is the largest number that divides evenly into both 30 and 20.
• It is denoted as HCF and helps in simplifying fractions and solving mathematical problems efficiently.

Lowest Common Multiple (LCM)

• The Lowest Common Multiple (LCM) is the smallest multiple that is common to two or more numbers.
• For instance, the LCM of 15 and 12 is 60 as it is the smallest number divisible by both 15 and 12.
• Also known as the Least Common Multiple, LCM aids in various mathematical operations such as adding fractions with different denominators.

The HCF and LCM

When dealing with fractions, the Highest Common Factor (HCF) and Lowest Common Multiple (LCM) play crucial roles in various mathematical operations. Understanding these concepts is essential for working with fractions effectively.

Definition and Importance

• The Highest Common Factor (HCF) is the largest number that divides two or more numbers without leaving a remainder. It is essential for simplifying fractions and finding common denominators.
• The Lowest Common Multiple (LCM) is the smallest multiple that is common to two or more numbers. It is vital for operations such as adding and subtracting fractions.

Finding HCF and LCM

• Factors and Multiples: HCF and LCM can be determined by listing the factors and multiples of the given numbers. For larger values, expressing numbers as a product of prime factors is a more efficient method.
• Example: For the number 12, the factors are 1, 2, 3, 4, 6, and 12. The prime factors of 12 are 2 and 3. Hence, 12 can be expressed as a product of its prime factors: 12 = 2 × 2 × 3.

Visualization with Venn Diagram

• A Venn diagram, a simple visual tool with overlapping circles, can be utilized to illustrate the relationships between different groups or sets. It is particularly useful for understanding the concepts of HCF and LCM visually.

Understanding Factors and Prime Factors

• Fractions
• Fractions are quantities that represent a part of a whole. When adding or subtracting fractions,
  • Use common denominators to perform operations.
• Finding Factors and Multiples
• Factors and multiples are essential in mathematics. To find them,
  • List all the factors and multiples of a number.
• Expressing Numbers as a Product of Prime Factors
• For larger numbers, expressing them as a product of prime factors is crucial. For instance, for the number 12:
  • The factors of 12 are 1, 2, 3, 4, 6, and 12.
  • The prime factors of 12 are 2 and 3.
  • 12 can be expressed as a product of its prime factors: 12 = 2 × 2 × 3.
• Efficient Methods
• Using prime factors to express numbers can simplify calculations. It helps in understanding the building blocks of a number and its divisors.
• Venn Diagrams
• A Venn diagram is a visual tool with overlapping circles that illustrates relationships between different sets or groups. It is useful for visualizing commonalities and differences.

Understanding Prime Factors in Detail

Utilizing Factor Trees for Prime Factorization

Knowing how to determine factors, use factor trees, and express numbers as products of prime factors is essential for finding common factors, calculating the Highest Common Factor (HCF), and the Lowest Common Multiple (LCM).

Summarized and Paraphrased Educational Content

How to Find Common Factors

• A common factor is a whole number that is a factor of two or more numbers. For instance, 2, 5, and 10 are common factors of 30 and 20.
• 1 is a common factor of all whole numbers.

Common Factors and Finding Them

A common factor is a whole number that divides evenly into two or more numbers without leaving a remainder. It is a number shared by multiple numbers as a factor.

• Definition: A common factor is a whole number that is a factor of two or more numbers.
• Example: In the numbers 30 and 20, common factors include 2, 5, and 10 since they can divide evenly into both 30 and 20.

Finding Common Factors:

To identify common factors between numbers:

• List the Factors: Begin by listing all the factors of each number.
• Comparison: Compare the factors of each number to identify numbers that appear in the factor lists of all numbers.

For instance, when finding common factors of 12 and 18:

• Factors of 12: 1, 2, 3, 4, 6, 12
• Factors of 18: 1, 2, 3, 6, 9, 18

In this case, the common factors between 12 and 18 are 1, 2, 3, and 6 as they are present in the factor lists of both numbers.

Common Factors and Lists

Examples

• Image caption: Find the common factors of 30 and 20

• Image caption: List the factors of 30 and the factors of 20

• Image caption: Compare the lists of factors to find numbers that occur in both lists. These are the common factors. The common factors of 30 and 20 are 1, 2, 5, and 10

• Image caption: Find the common factors of 24 and 25

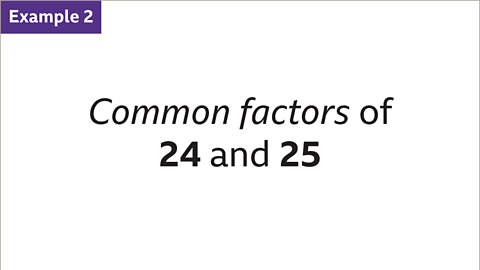
• Image caption: List the factors of 24 and the factors of 25

• Image caption: Compare the lists of factors to find numbers that occur in both lists. The only common factor of 24 and 25 is 1

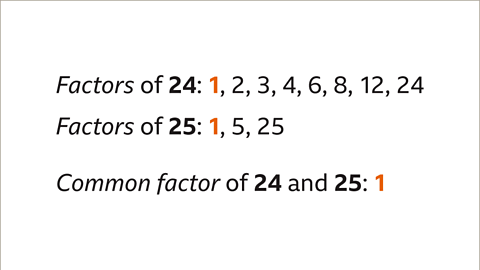
• Image caption: Find the common factors of 12, 36 and 60

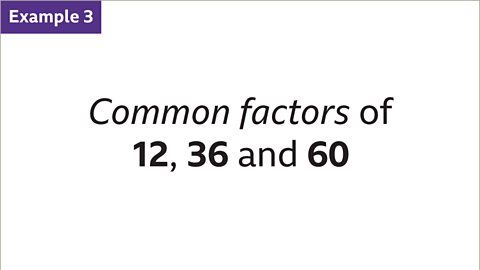
• Image caption: Find the common factors of 12, 36 and 60

Factors and Common Factors

• List the factors of 12, 36, and 60:
  • Factors of 12: 1, 2, 3, 4, 6, 12
  • Factors of 36: 1, 2, 3, 4, 6, 12, 18, 36
  • Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
• Compare the lists of factors to find common numbers:
  • Common factors of 12, 36, and 60: 1, 2, 3, 4, 6, 12
  • Since 12 is a factor of both 36 and 60, all factors of 12 are common factors of 36 and 60

Question

• Example 1: Common factors of thirty and twenty
• Find the common factors of 30 and 20

Back to top

Find the Highest Common Factor (HCF) of Numbers

• The Highest Common Factor (HCF) is the largest factor that divides into two or more numbers.
• For instance, the HCF of 30 and 20 is 10, denoted as HCF.
• To find the HCF, list the factors of the numbers. Prime factorisation can be used for larger numbers.

Prime Factorisation and Examples

• Expressing a number as a product of its prime factors is known as prime factorisation.
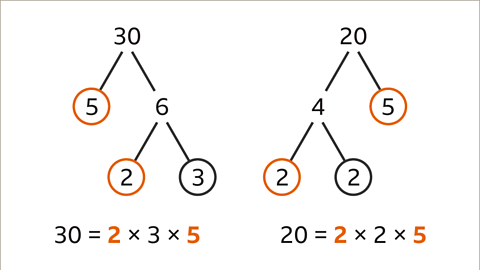
• For example, 30 can be expressed as 2 × 3 × 5, where 2, 3, and 5 are its prime factors.
• Considering 12, its factors are 1, 2, 3, 4, 6, and 12, with prime factors being 2 and 3. So, 12 = 2 × 2 × 3.

Prime Factorization

• Prime factorization involves expressing a number as a product of its prime factors. For instance, if we consider the number 30, its prime factorization is 30 = 2 × 3 × 5.

Understanding Prime Factorization

• Prime factorization is the process of breaking down a number into its prime factors, which are the fundamental building blocks of that number.
• It helps us understand the unique combination of prime numbers that make up a given number.
• For example, let's take the number 30. Its prime factors are 2, 3, and 5 because 30 = 2 × 3 × 5.

Product of Prime Factors

• When we talk about the product of prime factors, we are essentially looking at how a number can be expressed as a multiplication of its prime factors.

Understanding Product of Prime Factors

• For instance, let's consider the number 12. The factors of 12 include 1, 2, 3, 4, 6, and 12.
• However, the prime factors of 12 are 2 and 3. Therefore, 12 can be expressed as 12 = 2 × 2 × 3 when written as a product of its prime factors.
• This representation helps us see how a number can be broken down into its prime components.

Strategies for Finding Greatest Common Factor

• List the factors of each number.
• Compare the lists to find the greatest number common to both.

Prime Factorization Techniques

• Use the factor tree method to find prime factors of each number.
• Write each number as a product of its prime factors. This involves breaking down a number into its prime components.

Factor Tree Method

• Factor tree is a visual tool to determine the prime factors of a number by breaking it down into factor pairs.

Writing Numbers as Products of Prime Factors

• Expressing numbers as a multiplication of their prime factors simplifies calculations. For instance, 7³ represents 7 x 7 x 7.

Understanding Indices

• Indices are numbers positioned above and to the right of a base number, indicating repeated multiplication. For instance, 7³ represents 7 x 7 x 7.

Identifying Common Prime Factors

• Common prime factors are prime numbers that are shared among the factors of a given number. For example, the factors of 21 include 1, 3, 7, and 21. The common prime factors of 21 are 3 and 7 because they are prime numbers present in each product of prime factors.

Finding Highest Common Factor (HCF)

• To determine the Highest Common Factor (HCF), you multiply the common prime factors of the numbers involved.

Index Form and Highest Common Factor (HCF)

• Index Form: Index form is a shorthand notation for repeated multiplication. For instance, 5² means 5 × 5 and 5³ means 5 × 5 × 5.

Examples

• Find HCF by Listing: Determine the Highest Common Factor (HCF) of 30 and 20 by listing their factors.
• Factors Listing: List out the factors of 30 and 20.
• Comparing Factors: Compare the lists of factors to identify the greatest common factor. In this case, the HCF of 30 and 20 is 10.
• Prime Factorisation: Calculate the HCF of 30 and 20 using prime factorisation method.
• Factor Trees: Draw factor trees for 30 and 20, circle the prime factors, and express 30 and 20 as products of their prime factors.

Image Gallery

Understanding Common Prime Factors and Highest Common Factor (HCF)

Common prime factors and HCF play a crucial role in mathematics, especially when dealing with the relationship between numbers.

Identifying Common Prime Factors

• When finding the common prime factors of numbers like 30 and 20, we look for primes that both numbers share. For instance, the common prime factors of 30 and 20 are 2 and 5.

Finding the HCF through Common Prime Factors

• To determine the HCF of numbers like 30 and 20, we multiply their common prime factors. In this case, 2 x 5 = 10, making the HCF of 30 and 20 equal to 10.

Finding HCF with Completed Prime Factorization

• Even when numbers are already prime factorized, as in the case of 936 (2^3 * 3^2 * 13) and 810 (2 * 3^4 * 5), we can still find their HCF. By identifying common prime factors like 2 and 3, we calculate the HCF of 936 and 810.

Spotting Common Prime Factors

• Writing out the products of prime factors aids in identifying common primes. By expanding the factors, such as 936 as 2^3 * 3^2 * 13 and 810 as 2 * 3^4 * 5, we can easily spot common factors like 2 and 3.

Calculating HCF from Common Prime Factors

• When calculating the HCF of numbers like 936 and 810, multiply their common prime factors. For example, multiplying 2, 3, and 3 gives us an HCF of 18 for 936 and 810.

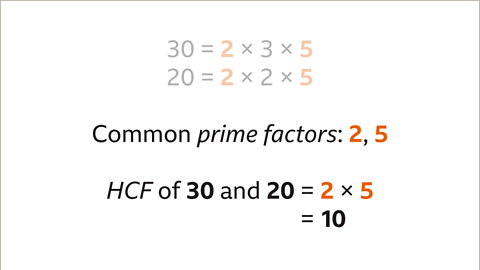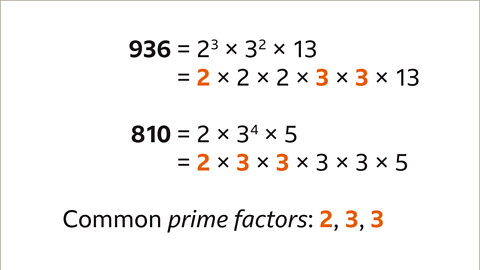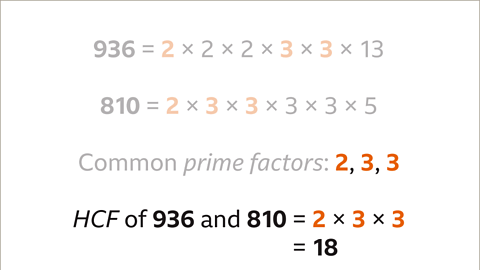Find the LCM of two or more numbers.

• A multiple is an integer that is in the multiplication table of a specific number. For example, 20 is a multiple of ten because 20 is in the ten times table.
• An integer that is in the multiplication table of a specific number can be positive, negative, or zero.
• The Lowest Common Multiple (LCM) is the lowest multiple that is common to two or more numbers. For instance, the LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables.
• LCM, also known as the Least Common Multiple, is the lowest multiple common to two or more numbers.

Multiples and Integers

An integer is any of the positive or negative whole numbers, including zero.

• Multiple: An integer that is in the multiplication table of a specific number. For instance, 20 is a multiple of ten because 20 appears in the ten times table.
• Lowest Common Multiple (LCM): The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 since it is the smallest value in both of their multiplication tables. It is also known as the least common multiple.

Lowest Common Multiple (LCM)

• The lowest common multiple (LCM) is the smallest multiple shared by two or more numbers.
• For instance, the LCM of 15 and 12 is 60 because it is the smallest number divisible by both 15 and 12.
• Another term for LCM is the least common multiple.
• To find the LCM of two or more numbers, you can list the numbers and identify their shared multiples.
• Prime factorization is a method to find the LCM for larger numbers by expressing them as a product of their prime factors.
• For example, if we take the number 30, its prime factorization is 2 × 3 × 5.

Prime Factorisation

Expressing a number as a product of its prime factors. For example, 30 written as a product of its prime factors is 30 = 2 × 3 × 5.

By Listing

• List consecutive multiples for each number. For instance, multiples of 3 are 3, 6, 9, 12, etc.
• The first multiple to occur in every list is the Least Common Multiple (LCM).

By Prime Factorisation

• Draw a factor tree for each number, a method to find the prime factors of a number by finding factor pairs.
• Write each number as a product of prime factors. For example, the prime factors of 12 are 2 and 3. 12 may be expressed as a product of its prime factors: 12 = 2 × 2 × 3.

Product of Prime Factors

• Identify the common prime factors in each product of prime factor. These are the factors of a number that are prime. For example, the factors of 21 include 1, 3, 7, and 21. The prime factors of 21 are 3 and 7.

Index

• Index is positioned above and to the right of a number, representing repeated multiplication. For instance, 7^3 signifies 7 x 7 x 7.

Understanding Prime Factors and LCM

Prime factorization is the process of determining the prime factors of a number, which are the factors that are prime numbers themselves. For instance, when considering the number 21, its factors include 1, 3, 7, and 21. However, the prime factors of 21 specifically are 3 and 7.

• The prime factors that are unique to each product play a crucial role in determining the distinctiveness of that number.
• To calculate the Least Common Multiple (LCM) of two numbers, multiply the common factors by the unique factors of one number and the unique factors of the other number.

Examples

Let's explore an example to solidify our understanding:

• Consider finding the LCM of 30 and 20. To do this, list the multiples of each number and identify the common and unique factors.

By following these steps, we can efficiently determine the LCM of any given pair of numbers.

Understanding Least Common Multiple (LCM)

The Least Common Multiple (LCM) is the smallest multiple that is shared by two or more numbers.

Using Consecutive Multiples

• When finding the LCM, you can list consecutive multiples of the numbers until you find a matching multiple.
• For instance, the LCM of 3 and 20 is 60, as it is the first number they both share as a multiple.

Prime Factorization Method

• Another method to find the LCM is through prime factorization.
• This involves breaking down the numbers into their prime factors and then multiplying the highest power of all factors.

Factor Trees for Prime Factors

• Creating factor trees helps in visualizing the prime factors of numbers.
• For example, for 30 and 20, factor trees can be drawn to represent how the numbers break down into primes.

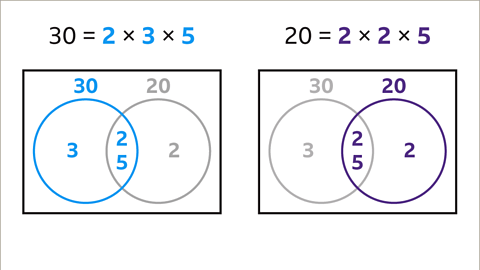
Identifying Common and Unique Factors

• After finding the prime factors, common factors are those shared by both numbers.
• Unique factors are specific to each number, not shared with the other.
• For 30 (2 x 3 x 5) and 20 (2 x 2 x 5), common factors are highlighted in orange, while unique factors are highlighted in blue and purple for 30 and 20 respectively.

Paraphrased Educational Content on Finding LCM

Understanding Prime Factors and LCM

• Prime factors are the building blocks of numbers. They are the prime numbers that multiply to give the original number.
• When finding the Least Common Multiple (LCM), we need to consider the common and unique prime factors of the numbers involved.

Example: Finding LCM of 30 and 20

• For numbers 30 and 20, the common prime factors are 2 and 5.
• The unique prime factor of 30 is 3, and of 20 is 2.
• To find the LCM, we multiply the common prime factors with the unique prime factors: 2 x 5 x 3 x 2 = 60.
• Therefore, the LCM of 30 and 20 is 60.

Example: Finding LCM of 936 and 810

• Given 936 = 2^3 x 3^2 x 13 and 810 = 2 x 3^4 x 5, we can find their LCM.
• By calculating the product, we get the LCM of 936 and 810.

Recognizing Common Prime Factors

• Writing the prime factors without index notation helps identify common factors easily.
• For instance, in the case of 936 and 810, the common prime factors are 2, 3, and 3.

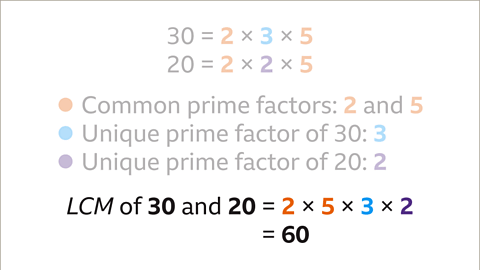Understanding the Lowest Common Multiple (LCM)

When we talk about finding the LCM of two numbers, such as 936 and 810, what we are essentially looking for is the smallest multiple that both numbers share.

Finding the LCM of 936 and 810

• Start by identifying the prime factors of each number:
• For 936, the prime factors are 2, 2, 3, 13.
• For 810, the prime factors are 2, 3, 3, 5.
• Multiply the common prime factors and unique prime factors of both numbers:
• 2 × 3 × 3 × 2 × 2 × 13 × 3 × 3 × 5 = 42,120.
• Therefore, the LCM of 936 and 810 is 42,120.

Example: Finding LCM of 30 and 20

• To find the LCM of 30 and 20:
• List the multiples of each number:
• Multiples of 30: 30, 60, 90, ...
• Multiples of 20: 20, 40, 60, ...
• The smallest common multiple is 60.

Question

Now, let's apply this concept to solve the following question:

How to use a Venn diagram to find the HCF and LCM

To use a Venn diagram, a simple visual diagram with overlapping circles, used to show the relationships between two different groups or sets, to find the HCF and LCM of two numbers:

• Write each number as a product of prime factors: The factors of 12 are 1, 2, 3, 4, 6, and 12. The prime factors of 12 are 2 and 3. 12 may be expressed as a product of its prime factors: 12 = 2 x 2 x 3 without using index form.
• Draw a Venn diagram:

• When finding the factors of numbers, draw a circle for each number.
• Identify the factors that both numbers have in common and place them in the intersection of the circles.
• Allocate the remaining prime factors unique to the first number in its respective circle.
• For the second number, place the remaining prime factors in its circle.
• Ensure each circle contains the complete prime factorization of the number.

Prime Factorization

• Prime factorization involves expressing a number as a product of its prime factors. For instance, 30 can be represented as 2 x 3 x 5.

Finding HCF and LCM

• To determine the Highest Common Factor (HCF) of numbers, multiply the numbers in the intersection.
• To find the Least Common Multiple (LCM) of numbers, multiply all the numbers within the circles in the Venn diagram.

Examples

• In an example where we need to find the HCF and LCM of 30 and 20 using a Venn diagram, we observe the following steps.

In this scenario, we analyze the Venn diagram to determine both the Highest Common Factor (HCF) and the Least Common Multiple (LCM) of the numbers 30 and 20.

Prime Factorization and HCF

Prime factorization is a fundamental concept in mathematics that involves breaking down a number into a product of its prime factors.

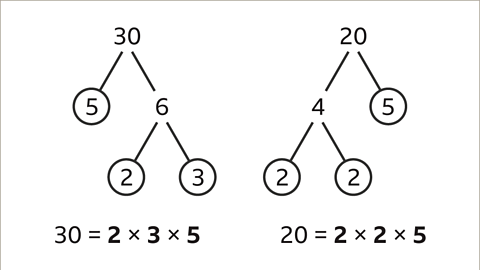
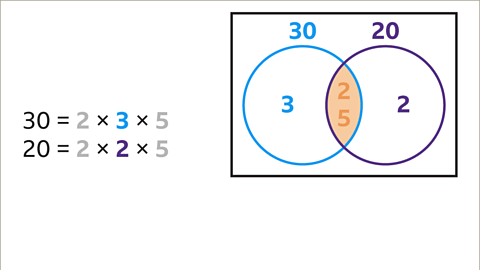
Factorization of 30 and 20

• When we look at the numbers 30 and 20, we can express them as products of their prime factors. For instance, 30 can be written as 2 x 3 x 5 and 20 can be written as 2 x 2 x 5.
• Visualizing this information can be aided by a Venn diagram. We represent 30 and 20 in separate circles within the diagram.

Common Factors and HCF

• Identifying the common prime factors of 30 and 20, which are 2 and 5, we place them in the intersection of the Venn diagram.
• To find the Highest Common Factor (HCF) of 30 and 20, we multiply these common prime factors, resulting in 10 as the HCF.

Remaining Prime Factors

• After determining the common factors, we place the remaining prime factors for 30 (3) and 20 (2) in their respective circles within the Venn diagram.

Verification and Completion

• It's crucial to ensure that each circle in the Venn diagram contains all the prime factors corresponding to the original numbers, confirming the accuracy of our factorization.

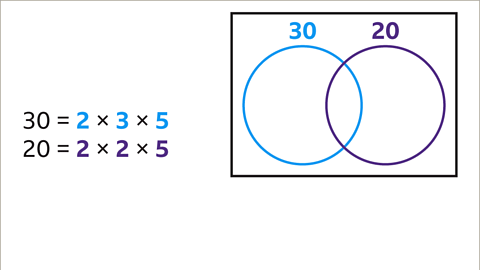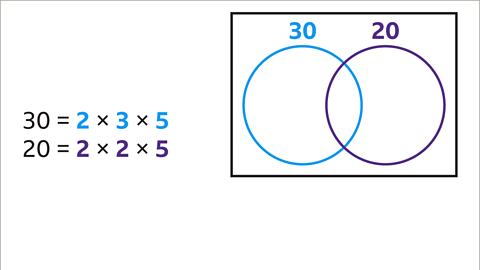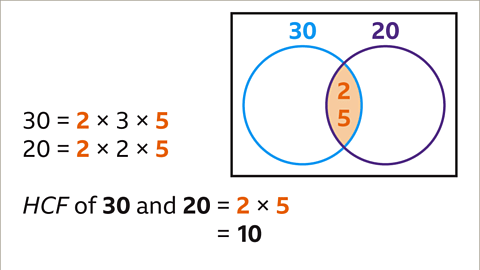Explanation of HCF and LCM Calculation using Venn Diagram

• When finding the Least Common Multiple (LCM) of numbers like 30 and 20, it involves identifying all the prime factors in a Venn diagram and multiplying them together. In the given example, the LCM of 30 and 20 is calculated as 2 x 5 x 3 x 2, which equals 60.

Example - HCF and LCM Calculation with Venn Diagram

• Consider a diagram representing two circles overlapping, with one labeled "thirty" and the other "twenty." To determine both the Highest Common Factor (HCF) and LCM of 30 and 20 using a Venn diagram, follow these steps:
• Examine the common and unique factors shared between the numbers 30 and 20 within the circles.
• Calculate the HCF by identifying the greatest common factor shared by both numbers.
• Calculate the LCM by multiplying all prime factors present in the Venn diagram.

Question

• How can Venn diagrams aid in the visualization and calculation of HCF and LCM for given numbers? Provide a step-by-step explanation.

• Practise common factors

  Practice identifying common factors and multiples by working through this quiz. Have a pen and paper ready for some questions.

• Quiz

• Real-world math

  

  The Highest Common Factor (HCF) and Lowest Common Multiple (LCM) are essential in various business scenarios for efficient material and stock management.

  HCF (Highest Common Factor) The HCF calculation aids businesses like a stationery shop in optimizing material usage. For instance, when producing cards with 24-inch and 36-inch card stock, having an HCF of 12 allows them to minimize waste by creating cards of 12 inches.

  LCM (Lowest Common Multiple) Calculating the LCM helps event planners streamline expenses. For example, if stickers come in packs of 15 and gift bags in packs of 6, buying in multiples of 30 (LCM of 15 and 6) ensures they have equal quantities for gift bags.

  

• Game - Divided Islands