How to Find Equivalent Fractions - Year 7 PDF Download
Key points
- Fractions are considered equivalent when they hold the same value. An equivalent fraction is a fraction that is equal in value to another fraction.
- A key characteristic of equivalent fractions is that they may have different numerators and denominators:
- The numerator of a fraction is the number written at the top, representing the parts used. For instance, in the fraction 1/3, the numerator is 1.
- The denominator of a fraction is the number written at the bottom, denoting the total number of equal parts. In the fraction 1/3, the denominator is 3.
Equivalent fractions can be determined through various methods:
| Method | Description |
|---|---|
| Multiplication | Multiplying both the numerator and denominator of a fraction by the same non-zero number results in an equivalent fraction. For example, multiplying 1/2 by 2/2 gives 2/4, which is equivalent to 1/2. |
| Division | Dividing both the numerator and denominator of a fraction by the same non-zero number yields an equivalent fraction. Dividing 6/8 by 2/2 provides 3/4, which is equivalent to 6/8. |
- Representation using Bar Model or Fraction Wall
- Multiplying both Numerator and Denominator of a Fraction by the Same Number
- Dividing both Numerator and Denominator of a Fraction by a Common Factor
Representation using Bar Model or Fraction Wall
- Bar models or fraction walls are visual tools that help in understanding equivalent fractions.
- For example, if you have a fraction like 1/2, you can represent it using a bar model by dividing a whole into two equal parts.
- Similarly, a fraction wall can show how different fractions relate to each other visually.
Multiplying Numerator and Denominator by the Same Number
- To find equivalent fractions, you can multiply both the numerator and denominator of a fraction by the same number.
- For instance, if you have the fraction 1/2 and you multiply both the numerator and denominator by 2, you get 2/4, which is equivalent.
- This process does not change the value of the fraction but only changes its representation.
Dividing Numerator and Denominator by a Common Factor
- Another way to find equivalent fractions is by dividing both the numerator and denominator of a fraction by a common factor.
- A common factor is a whole number that divides evenly into both the numerator and denominator.
- For example, if you have the fraction 4/8, both 4 and 8 can be divided by 4 to get the equivalent fraction 1/2.
Understanding common factors can be helpful in determining equivalent fractions.
How to find equivalent fractions
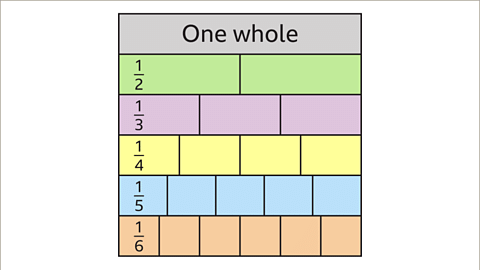
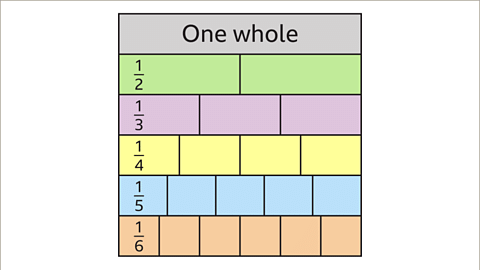
A fraction wall is a visual tool made up of bars of equal length, with each complete bar representing one whole. This tool is used to compare fractions by visually representing them.
Fraction Wall
A fraction wall consists of a set of bar models that represent different fractions. By using a fraction wall, fractions can be compared effectively.
Equal Length
When fractions are aligned on a fraction wall, they are of equal length, emphasizing their equivalence in value.
Steps to Find Equivalent Fractions on a Fraction Wall:
- Locate the fraction on the fraction wall.
- Draw a vertical line to the right of the fraction.
- Any equivalent fraction with the same value will align with this line.
By following these steps, you can easily identify equivalent fractions on a fraction wall. This visual method simplifies the concept of equivalent fractions and aids in understanding the relationship between different fractional values.
Equivalent Fractions
A fraction with the same value as another.
Example: Using a Fraction Wall
Image gallery. Skip image gallery.
- Image caption: A fraction wall can be used to compare fractions and find equivalent fractions.
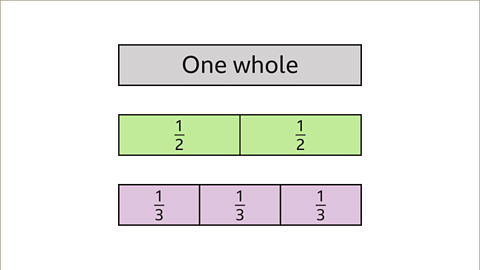
- Image caption: One whole is the same as two halves. It is also the same as three thirds.
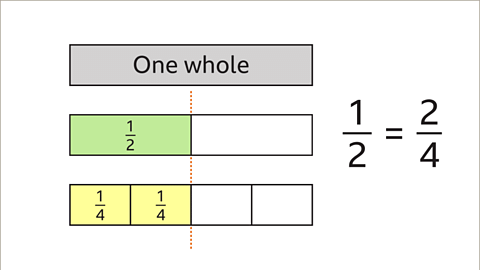
- Image caption: 1/2 is equivalent to 2/4. Both fractions have the same value.
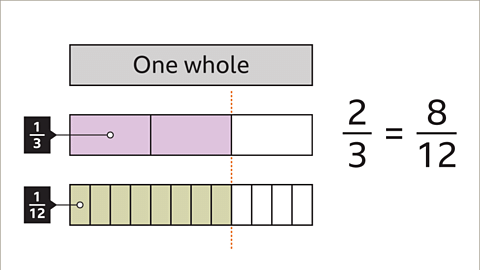
- Image caption: 2/3 is equivalent to 8/12. Both fractions have the same value.
- Image caption: Create a fraction wall by starting with one whole. Then create several bars split into 2, 3, 4, 5 and 6 equal parts. This can be extended to include more rows when necessary.
Fractions Equivalence Explained
- Image caption: What fractions are equivalent to 1/2?
- Explanation: Various fractions can be equivalent to 1/2, such as 2/4 and 3/6. When represented on a fraction wall, these fractions align to the right of 1/2, showcasing their equivalence.
- Image caption: Draw a line to the right of 1/2 on the fraction wall
- Explanation: Placing a line to the right of 1/2 on a fraction wall illustrates the equivalence of 1/2 to fractions like 2/4 and 3/6. This visual representation aids in understanding how different fractions relate to one another.
About Fraction Walls
- Definition: A fraction wall is a visual tool comprising rows representing fractions from one whole down to one sixth.
- Usage: Fraction walls serve as aids for comparing fractions and identifying equivalent fractions efficiently.
| Slide 1 of 7 | A fraction wall with six rows going from one whole down to one sixth. |
| A fraction wall can be used to compare fractions and find equivalent fractions. |
Back to top
How to create equivalent fractions
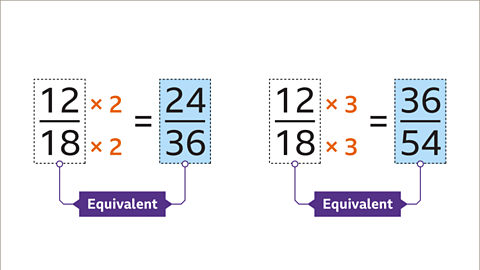
Creating equivalent fractions using multiplication and division:- Multiply both the numerator and the denominator by the same number. This process generates an infinite number of equivalent fractions, which are fractions with the same value as the original one.
- Divide both the numerator and denominator by a common factor, which is a whole number that is a factor of both numbers. For instance, 2, 5, and 10 are common factors of 30 and 20. There may be multiple common factors to consider.
To decide if two fractions are equivalent:
Compare the fractions by simplifying them and checking if they represent the same value. If the simplified forms of two fractions are equal, then they are considered equivalent.
Simplifying Fractions
- When we simplify a fraction, we aim to reduce it to its simplest form, also known as its lowest terms.
- To simplify a fraction, we divide both the numerator and the denominator by their highest common factor (HCF).
Explanation
Simplifying a fraction involves reducing it to its simplest form by dividing both the numerator and denominator by the highest common factor (HCF) of the two numbers. The HCF is the largest factor that can divide evenly into both numbers.
Example
For instance, if we have the fraction 30/20, the HCF of 30 and 20 is 10. By dividing both the numerator and denominator by 10, we get the simplified fraction 3/2.
Comparing Simplified Fractions
- After simplifying fractions, it's important to compare them to determine their relative sizes.
Understanding Equivalent Fractions
Using Multiplication and Division
Image gallerySkip image gallery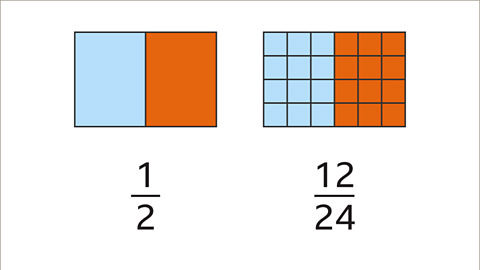
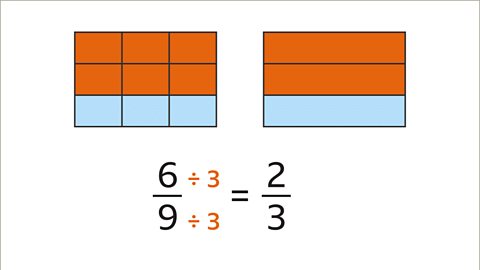
| Original Fraction | Equivalent Fraction |
|---|---|
| 1/2 | 12/24 |
| 6/9 | 2/3 |
| 12/18 | 4/6 |
Are 14/20 and 35/50 Equivalent Fractions?
- Both 14/20 and 35/50 simplify to 7/10. This means that these fractions are equivalent because they represent the same value.
The Simplification Process
- To simplify 14/20, you can find the highest common factor (HCF) of 14 and 20, which is 2. Dividing both the numerator and denominator by 2 gives us 7/10.
- Similarly, for 35/50, the HCF of 35 and 50 is 5. Dividing both numbers by 5 also results in 7/10.
Illustrative Example
- When you divide the numerator and denominator of 14/20 by 2, you get 7/10. Likewise, dividing 35/50 by 5 also yields 7/10.
Understanding Equivalent Fractions with Visuals
- Visual representations can help us grasp the concept of equivalent fractions more easily. For instance, images showing shaded parts of rectangles can demonstrate how 1/2 is equivalent to 12/24.
| Slide 1 of 8 | Two rectangles with parts shaded. On the left, a diagram with one half shaded. On the right, a diagram with twelve twenty-fourths shaded. 1/2 is equivalent to 12/24. |
Back to top
How to work out a missing value in an equivalent fraction
To determine the value of a missing numerator:
numerator- Identify the multiplier or divisor: The number that another number is multiplied by or divided by. For instance, in the calculation 4 x 5, the multiplier is 5. Similarly, in 30 ÷ 6, the divisor is 6 by dividing the larger denominator by the smaller denominator.
Identify the multiplier or divisor: The number that another number is multiplied by or divided by. For instance, in the calculation 4 x 5, the multiplier is 5. Similarly, in 30 ÷ 6, the divisor is 6 by dividing the larger denominator by the smaller denominator.
- To find the numerator for the larger denominator, multiply it by the determined number.
To find the numerator for the larger denominator, multiply it by the determined number.
Tips for Finding Numerator and Denominator
- To determine the numerator for the smaller denominator, divide by the obtained number.
- For finding the numerator for the smaller denominator, divide by the calculated number.
- To establish the value of a missing denominator:
- Find the multiplier/divisor by dividing the larger numerator by the smaller numerator.
- To find the denominator for the larger numerator, multiply by the identified number.
- To find the denominator for the smaller numerator, divide by the identified number.
Examples: Missing Values
Image GallerySkip Image Gallery- Image Caption: These are equivalent fractions with one value missing.
- Image Caption: The two fractions are equivalent. Find the missing numerator.
- Image Caption: Divide the larger denominator by the smaller denominator. 45 divided by 9 is 5. 5 is the multiplier. Both the numerator and denominator should be multiplied by 5.
 Image Caption: These are equivalent fractions with one value missing.
Image Caption: These are equivalent fractions with one value missing.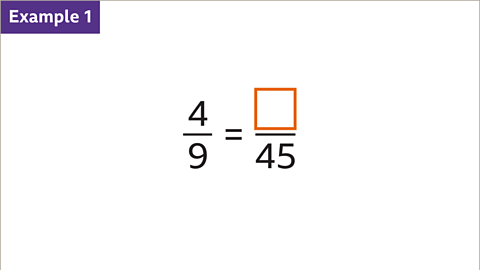
 Image Caption: The two fractions are equivalent. Find the missing numerator.
Image Caption: The two fractions are equivalent. Find the missing numerator.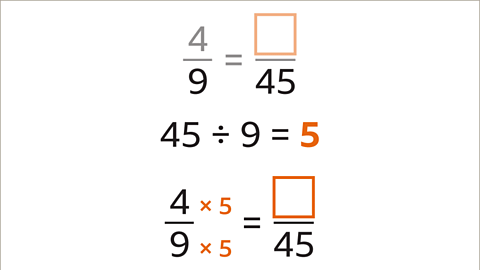
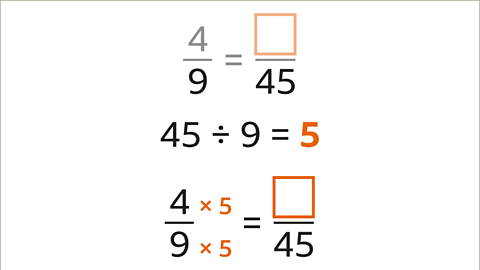
Understanding Equivalent Fractions
- When you multiply the numerator and denominator of a fraction by the same number, the fraction remains equivalent. For example, multiplying 4 by 5 gives 20. Therefore, 4/9 and 20/45 are equivalent.
- To find a missing denominator when two fractions are equivalent, consider the example of 27/36 and 9/something. Here, the missing denominator is 12, making the fractions equivalent.
- Dividing both the numerator and denominator of a fraction by the same number keeps the fraction equivalent. In the case of 27/36, dividing by 3 results in 9/12, which are equivalent fractions.
- Another instance is with 90/99 and 20/something. By dividing both the numerator and denominator by 9 and then multiplying by 2, you find the missing denominator to be 20, making the fractions equivalent.
Illustrative Examples
Example 1:
Consider the fractions 4/9 and 20/45. When you multiply the numerator and denominator of 4/9 by 5, you get 20/45, showing their equivalence.
Example 2:
For the fractions 27/36 and 9/something, the missing denominator is found to be 12, establishing their equivalence.
Example 3:
When dealing with 90/99 and 20/something, dividing by 9 and then multiplying by 2 reveals the missing denominator as 20, making the fractions equivalent.
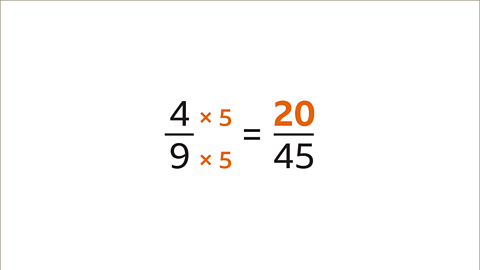 |  | 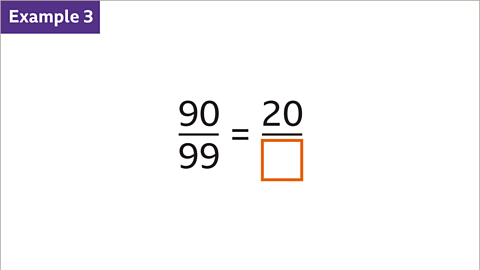 |
Understanding Equivalent Fractions
Equivalent fractions are fractions that represent the same proportion of a whole, even though they may look different.
Key Concepts:
- When you divide both the numerator and denominator of a fraction by the same number, you get an equivalent fraction.
- For instance, when 90 is divided by 9, the result is 10; similarly, 99 divided by 9 gives 11.
- Multiplying the resulting numerator and denominator by the same number maintains the fraction's value.
- In the given example, 10 multiplied by 2 equals 20, and 11 multiplied by 2 equals 22, making the missing denominator 22.
- The fractions 90/99 and 20/22 are equivalent because they represent the same portion of a whole.
Visual Representation:
Visual aids can help in understanding equivalent fractions better. The diagrams provided depict fractions and their equivalent forms.
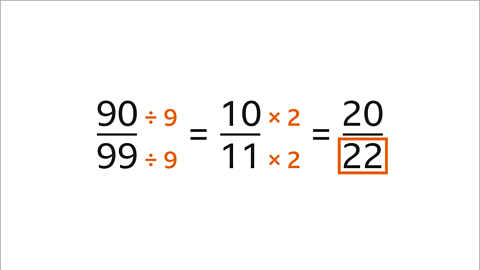 | 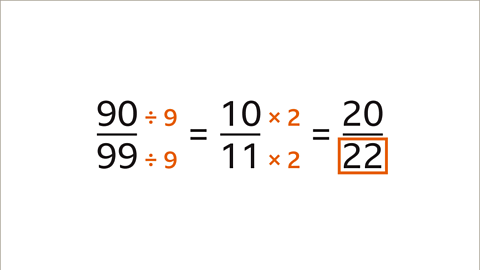 |
| Image Caption: The images illustrate equivalent fractions, showing the process of dividing and multiplying to maintain equivalence. | |
Practical Application:
Understanding equivalent fractions is essential in various real-world scenarios, such as dividing ingredients in a recipe or comparing sizes of different portions.
Exploring Fraction Equivalence
Equivalent fractions play a crucial role in mathematics, enabling us to compare and manipulate fractions effectively.
Benefits of Understanding:
- Knowledge of equivalent fractions simplifies operations like addition, subtraction, and comparison.
- It forms the basis for more advanced concepts in mathematics, such as converting between fractions and decimals.
Application in Daily Life:
Recognizing equivalent fractions can help in everyday situations, like sharing food items equally among friends or siblings.
Practise equivalent fractions
Try this quiz to practice finding and creating equivalent fractions.
Quiz
- Equivalent fractions are fractions that represent the same proportion of a whole.
- They have different numerators and denominators but represent the same value.
- For example, 1/2 and 2/4 are equivalent fractions because they both represent half of a whole.
Real-world maths
 Image caption
Image caption- Equivalent fractions find application in industries like architecture.
- Architects use equivalent fractions when preparing scale models and drawings.
- They ensure that proportions are accurately represented in their designs using fractions.
- Equivalent fractions are also practical in cooking and baking.
- Cooks may adjust recipes by using equivalent fractions.
- For instance, modifying a cupcake recipe from making 24 to 12 cupcakes involves adjusting ingredient quantities proportionately.
 Image caption
Image captionGame - Divided Islands
- Divided Islands is a game that involves splitting land masses into fractions.
- Players navigate challenges where they need to divide territories into equal parts.
- Understanding fractions is key to solving puzzles and progressing in the game.














