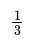Mixed numbers, proper and improper fractions - Year 7 PDF Download
Key points
- There are various kinds of fractions:
- Proper fraction: A fraction where the numerator is smaller than the denominator, for example, 3/5.
- Improper fraction: A fraction where the numerator is larger than the denominator, for instance, 9/4.
- Mixed number: A number represented using a whole number and a fraction, like 3 4/5.
Let's delve deeper into each type of fraction:
- Proper fraction: In a proper fraction, the numerator is less than the denominator. For example, 3/5 is a proper fraction because 3 is less than 5.
- Improper fraction: On the contrary, an improper fraction has a numerator greater than the denominator. An instance is 9/4, where 9 is more significant than 4.
- Mixed number: This type combines a whole number and a fraction. For instance, 3 4/5 comprises the whole number 3 and the fraction 4/5.
Understanding these distinctions is crucial when working with fractions, as they dictate how we interpret and operate with these numerical representations.
Understanding Fractions
- Proper FractionsA proper fraction consists of a numerator (the number above the fraction line) and a denominator (the number below the fraction line).The numerator represents the parts taken, while the denominator signifies the total number of equal parts.For instance, in 1/3, 1 is the numerator and 3 is the denominator.
- Improper FractionsAn improper fraction has a numerator larger than its denominator, always greater than one whole.
- Mixed NumbersA mixed number combines an integer with a fraction, written next to each other.It represents any positive or negative whole number, including zero.
- Fractions Representation
- Calculation Methods
Proper Fractions
- A proper fraction has a numerator indicating the parts taken and a denominator representing the total parts.
- The numerator is always less than the denominator.
- Example: In 1/3, 1 is the numerator, and 3 is the denominator.
Improper Fractions
- An improper fraction's numerator is greater than its denominator, always representing more than one whole unit.
Mixed Numbers
- A mixed number combines an integer with a fraction, written together.
- It represents any positive or negative whole number, including zero.
Fractions Representation
- Proper fractions, improper fractions, and mixed numbers can be depicted visually or in numerical form.
Calculation Methods
- When multiplying and dividing, improper fractions are typically used.
- For addition and subtraction, mixed numbers are often preferred.
What are mixed numbers, proper and improper fractions?
- Proper Fraction: A proper fraction is a fraction where the numerator is smaller than the denominator. For instance, 3/5 is a proper fraction. In visual representations, proper fractions are depicted as parts of a whole.
- Improper Fraction: An improper fraction has a numerator that is greater than the denominator. An example would be 9/4. Improper fractions are illustrated as quantities larger than one whole unit in diagrams.
- Mixed Number: A mixed number combines a whole number and a fraction. For example, 3 4/5 is a mixed number. In diagrams, mixed numbers are shown as a blend of whole shapes and portions of a shape.
Understanding Types of Fractions
- A fraction can be categorized as either a proper fraction or an improper fraction. A proper fraction has a numerator smaller than the denominator, like 3/5.
- An improper fraction, on the other hand, has a numerator larger than the denominator, such as 9/4.
- In addition to proper and improper fractions, there exist mixed numbers. These are a combination of a whole number and a fraction, for instance, 3 4/5.
Visual Representation of Fractions
- Visual aids are often used to understand fractions better. For example, consider a fraction like 3/5. If you shade three out of five parts, you can see a visual representation of the fraction.
- Similarly, when dealing with an improper fraction like 9/4, shading nine out of four parts can help in visualizing the concept better.
Proper Fractions
- In a proper fraction, the numerator is smaller than the denominator. For instance, 3/5 denotes three parts out of a total of five.
Improper Fractions
- Conversely, an improper fraction features a numerator that is larger than the denominator. An example is 9/4, representing nine parts out of four.
Mixed Numbers
- Mixed numbers combine a whole number with a fraction. For example, 3 4/5 signifies three whole units and four-fifths of another unit.
Importance of Understanding Fractions
- Fractions are crucial in various real-world applications, such as cooking recipes, measurements, and financial calculations.
| 1 of 4 |
How to Convert a Mixed Number to an Improper Fraction
- Multiply the integer by the denominator and add the numerator. This calculation provides the numerator of the improper fraction.
- The denominator remains the same.
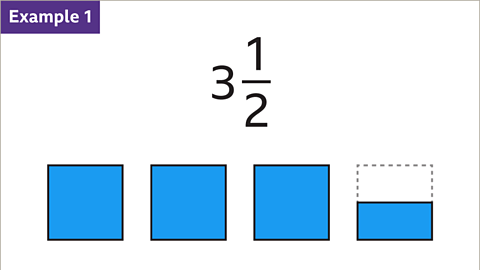
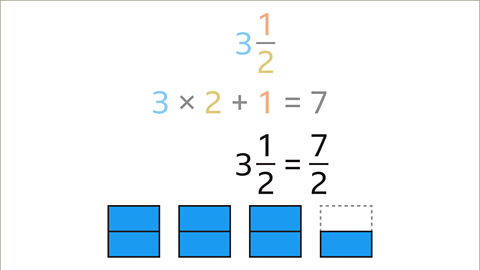
Example: Convert 3 1/2 and 5 2/9 to Improper Fractions
- Convert 3 1/2 to an improper fraction:
- Multiply the integer (3) by the denominator (2) and add the numerator (1). This results in 7, the numerator of the improper fraction.
- The denominator (2) remains unchanged. 3 1/2 converts to 7/2 as an improper fraction.
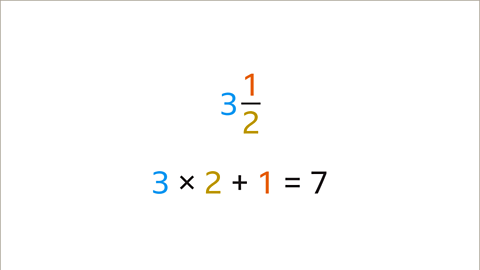
Converting Mixed Numbers to Improper Fractions
In this lesson, we will explore the process of converting mixed numbers to improper fractions.
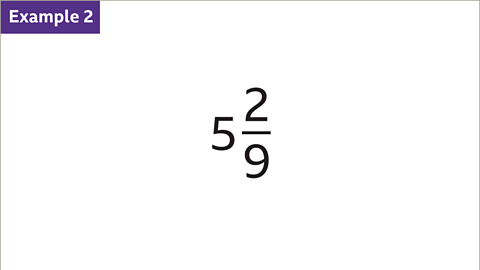
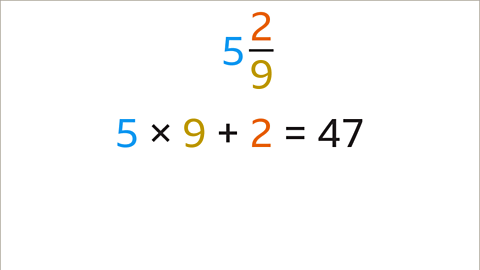
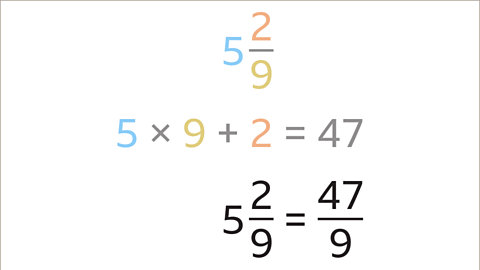
Question
Now, let's apply what we've learned to solve a few examples:
Example 1: A diagram shows three and one half in blue.
Slide 1 of 6
Example 1. A diagram shows three and one half in blue. The fraction three and one half is written above.
Back to top
How to Convert an Improper Fraction to a Mixed Number
- Start by dividing the numerator by the denominator. The numerator is the top number in a fraction, representing the number of parts considered. For example, in 1/3, the numerator is 1.
- Identify the Numerator and Denominator
- The numerator is the top number of a fraction, representing the parts considered, like 1 in 1/3.
- The denominator is the bottom number of a fraction, indicating the total number of equal parts, like 3 in 1/3.
- The whole number in a mixed number is the integer part, which does not have any fractional component.
- Understanding Integers
- Integers are positive or negative whole numbers, including zero, like -3, 0, 1, 27, etc.
- In a mixed number, the remainder is the amount left over after division. For instance, in 30 divided by 7, the result is 4 with a remainder of 2.
- Explaining Remainders
- The remainder is the leftover part after dividing one number by another. For example, when you divide 10 by 3, you get 3 with a remainder of 1.
- When converting an improper fraction to a mixed number, the denominator remains the same.
Converting Improper Fractions to Mixed Numbers
In mathematics, converting improper fractions to mixed numbers is a fundamental concept that involves transforming a fraction where the numerator is greater than or equal to the denominator into a whole number and a proper fraction part.
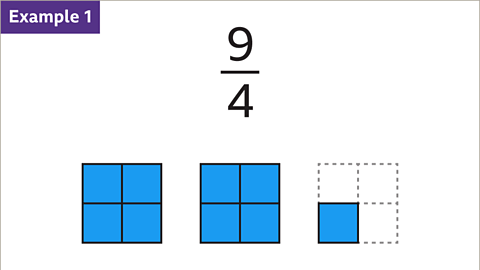
Example: Converting 9¼ and 23&frac46; to Mixed Numbers
- Convert 9¼ to a mixed number:
- Divide the numerator (9) by the denominator (4). 9 ÷ 4 = 2 remainder 1
- The whole number (2) becomes the integer part of the mixed number, and the remainder (1) is the numerator of the fraction. Therefore, 9¼ converts to 2¼ as a mixed number.
- Convert 23&frac46; to a mixed number:
- Divide the numerator (23) by the denominator (6). 23 ÷ 6 = 3 remainder 5
- The whole number (3) becomes the integer part of the mixed number, and the remainder (5) is the numerator of the fraction. Thus, 23&frac46; converts to 3⅚ as a mixed number.
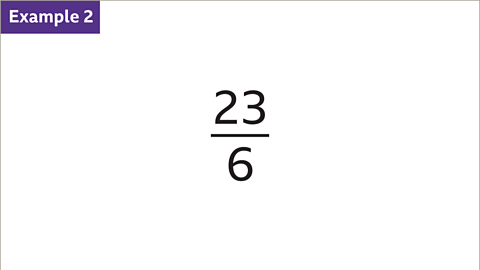
| Image caption | Convert 9¼ to a mixed number. |
| Image caption | Divide the numerator (9) by the denominator (4). 9 ÷ 4 = 2 remainder 1 |
| Image caption | The whole number (2) is the integer part of the mixed number. The remainder (1) is the numerator of the fraction. 9¼ converts to 2¼ as a mixed number. |
| Image caption | Convert 23&frac46; to a mixed number. |
| Image caption | Divide the numerator (23) by the denominator (6). 23 ÷ 6 = 3 remainder 5. The whole number (3) is the integer part of the mixed number. |
| Image caption | The remainder (5) is the numerator of the fraction. The denominator stays the same. 23&frac46; converts to 3⅚ as a mixed number. |
Practise converting mixed numbers and improper fractions
Try practicing recognizing and converting mixed numbers and improper fractions with this quiz. You might need a pen and paper to solve some of these questions.
Quiz
- Recognizing Mixed Numbers and Improper Fractions
- Understand the concept of mixed numbers and improper fractions.
- Identify when a fraction is in the form of a mixed number or an improper fraction.
- Practice converting between mixed numbers and improper fractions.
- Converting 9/4 to a Mixed Number
- Recognize that 9/4 is an improper fraction.
- Understand that 9/4 can be converted to a mixed number by dividing the numerator by the denominator.
- Example: 9/4 = 2 1/4 (two and one-fourth)
- Utilizing Quizzes for Practice
- Engage in quizzes to reinforce your understanding.
- Apply the concepts of mixed numbers and improper fractions in solving problems.
- Check your answers and understand any mistakes made.
Real-world Maths
 Image caption
Image caption- Mixed numbers and improper fractions are frequently utilized in real-life scenarios.
- For instance, motorway road signs typically display distances as whole numbers.
- On the contrary, road signs on smaller roads or rural routes often use mixed numbers due to shorter distances.
 Image caption
Image caption- Converting between mixed numbers and improper fractions is practical, especially when planning food quantities like pizzas for a party.
- Consider this scenario: Each person wants 2/3 of a pizza. If there are 20 people, that amounts to 40/3 pizzas. To simplify, this equals 6 whole pizzas with 2/3 remaining. To ensure enough pizza for the party, you'd need to purchase 7 pizzas.