Addition and Subtraction of Fractions - Year 7 PDF Download
Introduction
- Fractions can be added in various ways:
- When fractions share the same denominator, which is the number of equal parts in a whole (e.g., in 1/3, the denominator is 3), you simply add the numerators (the number of parts used) to get the total.
- For fractions with different denominators, equivalent fractions are utilized. These are fractions that have the same value but different representation. To add such fractions, first find the lowest common multiple (LCM) of the denominators. The LCM is the smallest number that both denominators can divide into evenly. By converting all fractions to equivalent fractions with the common denominator, you can then add them together.
- Improper fractions, where the numerator is greater than the denominator (e.g., 9/4), can be added directly as fractions or converted to mixed numbers (e.g., 3 1/4) and then added by separately adding the whole numbers and fraction parts.
- Adding mixed numbers involves adding the integer parts and the fractional parts independently.
- Understanding equivalent fractions and converting between improper fractions and mixed numbers is crucial for adding fractions effectively.
- Fractions Subtraction:
- Fractions can be subtracted when they share the same denominator, which is the number of equal parts in a fraction. For example, in 1/3, the denominator is 3.
- The difference between two numbers is the result of comparing their quantities. It is always a positive value. For instance, the difference between 3 and 5 is 2, and vice versa.
- When fractions have different denominators, they are converted into equivalent fractions with the same value. This involves changing the denominators to the lowest common multiple (LCM) they share.
- An improper fraction, where the numerator is greater than the denominator (e.g., 9/4), can be subtracted as they are.
- To find the difference between mixed numbers (a number written as a whole number and a fraction, e.g., 3 4/5), convert them to improper fractions first and then perform subtraction.
- When dealing with mixed numbers where the second fractional part is smaller than the first, subtract the integer and fractional parts separately.
Adding fractions with the same denominators
- When you are adding fractions with the same denominators, simply add the numerators together.
- Sometimes, the resulting fraction can be simplified to its lowest terms. This means reducing it to the simplest form.
- If your final answer is an improper fraction (where the numerator is greater than the denominator), you have the option to leave it as is or convert it into a mixed number.
Example
Example: Add the fractions.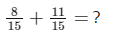 Sol:
Sol: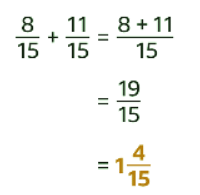
- The denominators are the same - the answer will be in fifteenths.
- Add the numerators. 8 + 11 = 19
- The sum is 19/15. This is
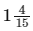 as a mixed number.
as a mixed number.
Adding fractions with different denominators
- Find the lowest common multiple (LCM) of the denominators.
- Rewrite the fractions as equivalent fractions with the same denominator.
- Add the numerators to find equivalent fractions.
- To simplify a fraction means to reduce it to its simplest form or lowest terms.
- Improper fractions have numerators greater than denominators.After adding fractions, consider whether to leave the answer as an improper fraction or convert it to a mixed number.
Any common multiple of the denominators can be used as the common denominator . However, the most efficient way of adding fractions with different denominators is to use the LCM.
Example
Example: Add the fractions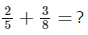
Sol: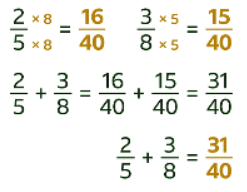
- Find the LCM. The LCM of 5 and 8 is 40
- Create equivalent fractions with a denominator of 40. 2/5 is equivalent to 16/40 and 3/8 is equivalent to 15/40
- Add the numerators. 16 + 15 = 31
- The fractions add up to 31/40
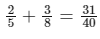
How to Add Improper Fractions and Mixed Numbers
To add improper fractions:
- The easiest method is to combine the improper fractions using a common denominator, which is a denominator shared by two or more fractions.
- Alternatively, you can transform the improper fractions into mixed numbers by dividing the numerator by the denominator. The whole number becomes the integer part of the mixed number, and the remainder serves as the numerator for the fraction.
When adding mixed numbers, follow these steps:
- Add the integers.
- Use the LCM of the denominators to rewrite the fractions as equivalent fractions with the same denominator.
- Add the fractions.
- Simplify the answer if possible.
- Alternatively, change the mixed numbers to improper fractions first and add the improper fractions using a common denominator.
Examples
Example 1: Add the mixed numbers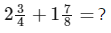 If the sum of two fractions gives an answer over 1 (an improper fraction), the calculation is completed by changing the improper fraction to a mixed number and adding the integers.
If the sum of two fractions gives an answer over 1 (an improper fraction), the calculation is completed by changing the improper fraction to a mixed number and adding the integers.
Sol: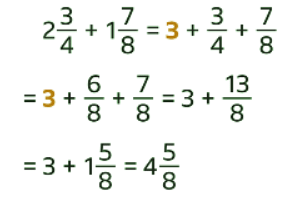
- Add the integers.
- Write the fractions with the same common denominator.
- Add the fractions.
- The answer is
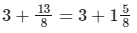
- The fractions add to over 1. Complete the calculation by adding
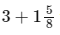 to give
to give 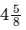
Example 2: Add the mixed numbers.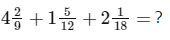 Sol:
Sol: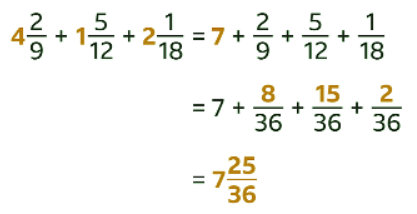
- Add the integers.
- The fractions have different denominators.
- The LCM of 9, 12 and 18 is 36. Rewrite the fractional parts with a denominator of 36. 2/9 is equivalent to 8/36, 5/12, is equivalent to 15/36 and 1/18 is equivalent to 2/36.
- Add the fractions.
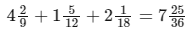
Real-world Maths
- Adding fractions can be used to combine measurements. This can be useful if, for example, you want to add a border to a photograph.
- A wide or narrow border can affect the look of a photo. These measurements may involve mixed numbers.
- For a picture measuring
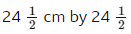 with a border of
with a border of 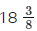 on each side, the total dimensions will be
on each side, the total dimensions will be 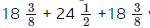 which is
which is 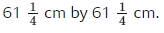
Subtracting Fractions with the Same Denominator
To find the difference between fractions with the same denominator, subtract the numerators. The denominator remains the same.
To subtract mixed numbers with the same denominators:
- Subtract the integers and subtract the fractions.
- When the fraction to be subtracted is larger than the first fraction, convert the mixed numbers to improper fractions first, then perform the subtraction.
- The answer can be kept as an improper fraction or converted to a mixed number if necessary.
Example
Example: Calculate 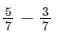
Sol: The denominators are the same. Subtract the numerators.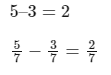
Subtracting fractions with different denominators
To subtract fractions with different denominators:
- Find the lowest common multiple (LCM) of the denominators.
- Rewrite the fractions as equivalent fractions with the same denominator.
- Complete the subtraction.
To subtract mixed numbers with different denominators:
- Subtract the integer
- Subtract the fractions using equivalent fractions with the same denominator.
To subtract mixed numbers with different denominators, when the second fraction is greater than the first fraction:
- Change the mixed numbers to improper fractions.
- Do the subtraction.
- The answer can be left as an improper fraction or changed to a mixed number if required.
Example
Example: Work out 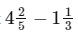
Sol: 
- The LCM of 3 and 5 is 15
- Write equivalent fractions with the same denominator for each mixed number. 2/5 is equivalent to 6/15. 1/3 is equivalent to 5/15
- Subtract the integers. 4 – 1 = 3
- Subtract the fractions.

Real-world maths
- Some countries use fractions in measurements when cooking and baking.
- These baking recipes measure ingredients in cups, such as 1/4 cup of butter or 1/2 cup of self-raising flour.
- People might subtract fractions when modifying recipes that use cups as a measurement. For example, if a recipe called for
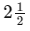 cups of flour, a baker might subtract 3/4 from
cups of flour, a baker might subtract 3/4 from 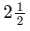 cups of flour and replace it with 3/4 cup of cocoa powder for a chocolate version.
cups of flour and replace it with 3/4 cup of cocoa powder for a chocolate version. - A baker might also subtract 1/4 from 1 cup of sugar if they wanted a less sugary version of the recipe.
FAQs on Addition and Subtraction of Fractions - Year 7
| 1. How do you add fractions with the same denominators? |  |
| 2. What is the process for adding fractions with different denominators? |  |
| 3. Can you explain how to add improper fractions and mixed numbers? |  |
| 4. How do you perform addition and subtraction of fractions? |  |
| 5. What are some tips for effectively adding fractions in Year 7? |  |



















