Introduction: Standard Index Form - Year 7 PDF Download
Key points
Standard form is a method used to express very large or very small numbers in a more manageable way. In standard form, numbers are written as a number between 1 and 10 multiplied by a power of ten. This representation is also known as standard index form or scientific notation.
Definition of Standard Form
Standard form simplifies the representation of extremely large or small numbers by breaking them down into a number between 1 and 10 multiplied by a power of ten.
- Example: The speed of light is approximately 3 x 108 meters per second.
Usage of Standard Form
Standard form is particularly useful in scientific notation and mathematical calculations involving very large or very small numbers.
- Example: The mass of an electron is about 9.11 x 10-31 kilograms.
- Example: The distance from the Earth to the Sun is roughly 1.496 x 1011 meters.
Representation of Numbers in Standard Form
Any number in standard form can be expressed as a number between 1 and 10 multiplied by a power of ten.
- Example: 6.02 x 1023 represents Avogadro's number in chemistry.
- Example: 2.998 x 108 meters per second is the speed of light in a vacuum.
Understanding Powers of 10
- A multiplied by 10 to the power of n represents a number that is equal to or greater than 1 and less than 10, where n is an integer. This can be any positive or negative whole number, including zero.
- For instance, the second power of 10 is 100. Powers of 10 include numbers like 10, 100, 1000, and so on, which you can multiply by to achieve the original value.
- The integer power of ten is positive for numbers greater than 10 and negative for values less than 1. When dealing with numbers between 1 and 10, the integer power of ten is zero.
- Understanding place value and operations involving multiplication and division by powers of ten is crucial for mastering this concept.
Illustrative Example
- If we consider the number 300 in standard form, it would be written as 3 x 10^2. Here, A equals 3 and n equals 2. This demonstrates how to express a number using powers of 10.
Understanding Integer Powers of Ten
- When we talk about the integer power of ten, it signifies how many times ten is multiplied by itself.
- For numbers greater than 10, the integer power of ten is positive. For instance, 1000 = 10 x 10 x 10, so the integer power of ten is 3.
- On the contrary, for values less than 1, the integer power of ten is negative. For example, 0.01 = 1 / (10 x 10), making the integer power of ten -2.
- Numbers falling between 1 and 10 have an integer power of ten equal to zero as there is no multiplication or division by ten involved.
Importance of Understanding Place Value
- Having a strong grasp of place value is crucial in mathematics as it determines the value of a digit based on its position in a number.
- Multiplying or dividing by powers of ten is a fundamental concept that helps in shifting digits to the left or right, altering the value of numbers significantly.
Video
Standard index form, which involves using powers of ten, plays a vital role in various fields, including computer game design.
In a video featuring games developer Shahan, he explains how standard index form is applied in his game development work, showcasing its practical significance.
How to write numbers in standard form
Standard form is a method used to represent extremely large or small numbers in a concise manner. It involves expressing a number as a value between 1 and 10 multiplied by a power of ten, also known as scientific notation.
Key Steps to Writing Numbers in Standard Form:
- Express the number as a value between 1 and 10. The first non-zero digit should be in the units column, followed by the decimal point and the remaining digits. Trailing zeros are unnecessary. If the number is a single digit, the decimal point is not required.
Illustrative Example:
Let's consider the number 0.0000456. To write this in standard form, we first express it as 4.56, moving the decimal point to the right to make the first non-zero digit the units digit. Then, we note that we have moved the decimal point four places to the right, so the number in standard form is 4.56 x 10-4.
Importance of Standard Form:
Standard form simplifies the representation of very large or very small numbers, making it easier to work with them in mathematical calculations and scientific contexts.
Powers of 10
Understanding Powers of 10
Powers of 10 represent how many times you multiply 10 by itself. When a number is greater than or equal to 10, the power is a positive integer, indicating how many times the value must be multiplied by 10 to get the original number.
Example of Positive Power
For instance, 1000 is greater than 10, so the power is positive. In standard form, 1000 is written as 1 x 10³.
Example of Zero Power
If a number is greater than or equal to 1 but less than 10, the power is zero. For example, 4 is between 1 and 10, so the power is 0. In standard form, 4 is written as 4 x 10⁰.
Example of Negative Power
When a number is less than 1, the power is a negative integer, indicating how many times the value must be divided by 10 to get the original number. For example, 0.001 is less than 1, so the power is negative. In standard form, 0.001 is written as 1 x 10⁻³.
- Understanding Powers in Standard Form
- For numbers greater than or equal to 10, the power is a positive integer. This means that any positive or negative whole number, including zero, can be a power. The power can be determined by counting the number of places the first non-zero digit has moved to the right. Essentially, this is the number of times the value must be multiplied by 10 to obtain the original number. For instance, consider 1000; since it is greater than 10, the power is positive. In standard form, 1000 is written as 1 x 103.
- For numbers greater than or equal to 1 and less than 10, the power is zero. Take the number 4, for example. It lies between 1 and 10, so its power is zero. In standard form, 4 is represented as 4 x 100.
- When dealing with numbers less than 1, the power is a negative integer. To find the power, count the number of places the first non-zero digit has shifted to the left. This indicates the number of times the value must be multiplied by (or divided by 10) to acquire the original number. For instance, 0.001 is less than 1, so the power is negative. In standard form, 0.001 is written as 1 x 10-3.
Understanding Powers in Standard Form
- For numbers greater than or equal to 1 and less than 10:
- When a number falls within this range, the power is zero. For instance, 4, being greater than 1 but less than 10, has a power of zero. In standard form, 4 is represented as 4 x 100.
- For numbers less than 1:
- The power is a negative integer, determined by the count of places the first non-zero digit moves to the left. This value signifies how many times the number must be multiplied or divided by 10 to return to the original number. For example, 0.001 is less than 1, hence the power is negative. In standard form, 0.001 is written as 1 x 10-3.
Examples
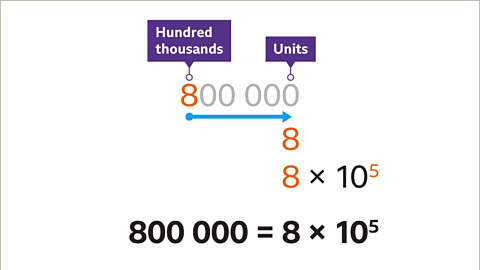
- Image Caption: Write 800,000 in standard form.
 Image caption, Write 800,000 in standard form.
Image caption, Write 800,000 in standard form.Converting Numbers into Standard Form
In mathematics, converting numbers into standard form is a crucial skill that helps us represent large or small numbers in a more concise manner. Let's delve into the process of converting numbers into standard form.
1. Writing Numbers in Standard Form
- When writing a number, such as 800,000, in standard form, we express it as a value between 1 and 10, multiplied by a power of 10.
- For example, 800,000 can be written as 8 × 10⁵ in standard form.
- The power of 10 is determined by the number of places the first non-zero digit has moved to the right.
2. Example: Converting 3⅘ into Standard Form
- Let's consider the number 3⅘ and convert it into standard form.
- To express 3⅘ in standard form, we analyze its value and rewrite it in a concise format.
- Through this process, we can better understand the concept of standard form and its application in mathematics.
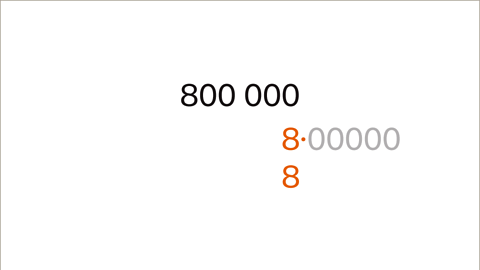 |  |
 |
Converting Numbers into Standard Form
Standard form is a way of writing down very large or very small numbers in a more concise and readable manner.
Writing Numbers Between 1 and 10
- When we write a number like 3.9, it lies between 1 and 10 because the first non-zero digit (3) is in the units column, followed by the decimal point. Hence, it's already between 1 and 10.
- For example, 3.9 can also be written as 3.9 × 10⁰ in standard form. Here, the power of ten is determined by the number of places the first non-zero digit has moved.
Converting Numbers to Standard Form
- Let's take the number 0.0007601 as an example. This number can be written in standard form as 7.601 × 10⁻⁴. The first non-zero digit (7) is in the units column, followed by the decimal point.
- Similarly, 0.0007601 can be expressed as a value between 1 and 10 because the first non-zero digit (7) is in the units column, followed by the decimal point.
| Image 1 | Image 2 |
|---|---|
 |  |
 |  |
Image caption
- When we write 0.007601, we express it as 7.601 × 10-3 in standard form.
- The power of ten is negative since 0.007601 is less than 1. The negative power signifies that the number is a fraction.
- To determine the power, we count how many places the first non-zero digit moves to the left. In this case, 7 moves three places from the thousandths to the units column.
- 0.007601 can be rewritten as 7.601 × 10-3 in scientific notation.


Write × 10
- Express numbers in the power of ten for standard form representation.
- A negative power indicates numbers less than 1.
- Example: 0.007601 = 7.601 × 10-3
Example 1: Eight-thousand
- Write 800,000 in standard form.
Question
Back to top
How to determine if two variables are directly proportional
To ascertain if two variables are directly proportional, you can follow the steps below:
- When one variable increases, the other also increases proportionally.
- When one variable decreases, the other also decreases proportionally.
Converting Standard Form Numbers to Ordinary Numbers
Converting a standard form number (A × 10^n) to an ordinary (decimal) number involves the following:
- When n is positive, the number is larger than A. Each digit in A moves n places to the left. Gaps are filled with zeros.
- When n is negative, the number is smaller than A. Each digit in A moves n places to the right. Gaps are filled with zeros.
- For n = 0, the ordinary number is simply the value of A.
Examples:
- Positive n example: A = 4.5 × 10^3 → A = 4500
- Negative n example: A = 3.2 × 10^(-2) → A = 0.032
Understanding the Movement of Digits with Powers of Ten
- When a digit in number A moves n places to the right, zeros fill the gaps between the digits and the decimal point.
- For instance, if each digit in A shifts n places to the right:
- The gaps between the digits of A and the decimal point are filled with placeholder zeros.
- When n equals zero, the value of A remains the same as the ordinary number.
Examples
Image gallery Skip image gallery- Image caption: Understanding Powers of Ten
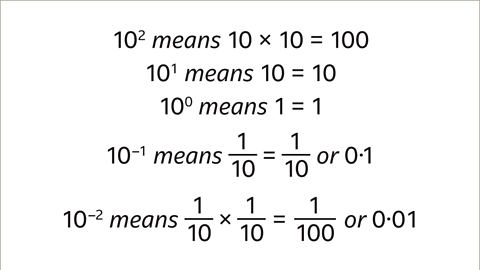 Image caption: Powers of ten.
Image caption: Powers of ten. - Image caption: Converting 9.72 × 10⁴ into a decimal number.
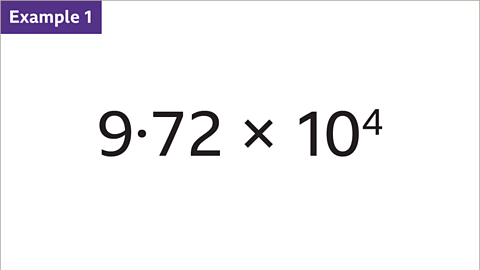
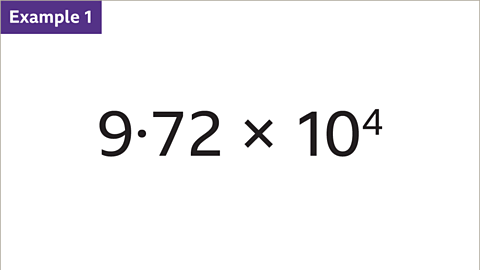 Image caption: Multiply A (9.72) by 10⁴. 10⁴ equals 10 × 10 × 10 × 10 or 10,000
Image caption: Multiply A (9.72) by 10⁴. 10⁴ equals 10 × 10 × 10 × 10 or 10,000- Image caption: Multiplying by 10,000 involves shifting each digit four places to the left. For example, 9 units become 90,000, 7 tenths become 7,000, and 2 hundredths become 200. Fill in zeros before the decimal point to maintain the number's value.
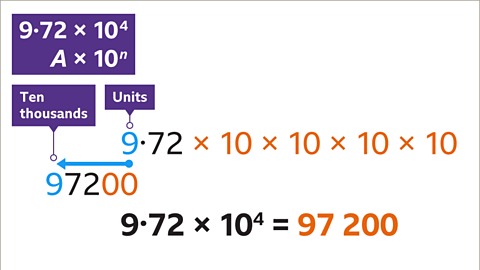
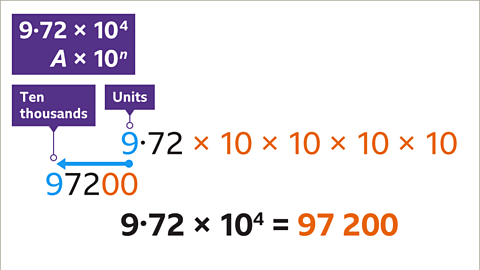 Image caption: Shifting digits to multiply by 10,000.
Image caption: Shifting digits to multiply by 10,000.Powers of Ten
Understanding how powers of ten work can simplify mathematical operations involving large or small numbers.
- Ten squared (102) equals 10 x 10 = 100. This demonstrates how multiplying a number by itself results in a larger value.
- Ten to the power of one (101) equals 10. This signifies that raising 10 to the power of 1 gives us 10 itself.
- Ten to the power of zero (100) equals 1. This rule highlights that any number raised to the power of zero equals 1.
- Ten to the power of negative one (10-1) equals 0.1. This showcases that a negative exponent corresponds to the reciprocal of the positive exponent.
- Ten to the power of negative two (10-2) equals 0.01. This illustrates how negative exponents lead to fractions and smaller values.
Multiplying by Powers of Ten
When we multiply a number by powers of ten, the placement of the decimal point shifts accordingly.
- To multiply by 10-2 (0.01), each digit moves two places to the right. For example, 8 becomes 0.08 and 1 becomes 0.01, with a placeholder zero added before the decimal point.
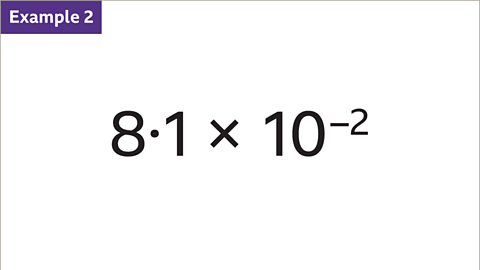 | 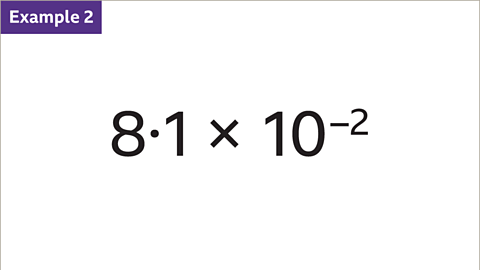 |
1 of 7
Slide 1 of 7: When we explore powers of ten, we see how each exponent affects the value, from magnifying it to making it smaller.
Question
Back to topHow to Compare and Order Numbers in Standard Form
To compare and order numbers in standard form:
It may be useful to review comparing and ordering decimals.
Examples
Image gallerySkip image gallery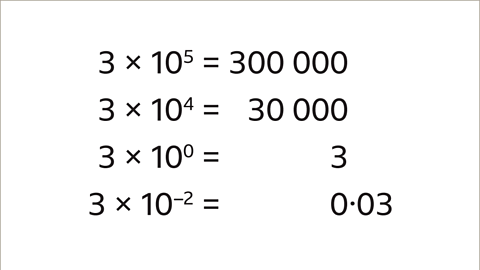 Image caption: The greater the power of ten, the greater the number.
Image caption: The greater the power of ten, the greater the number.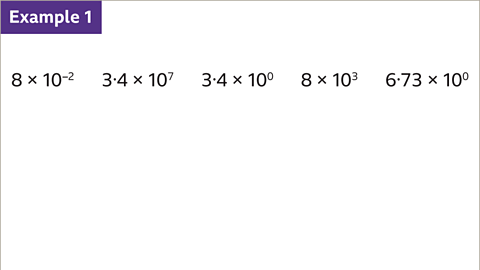
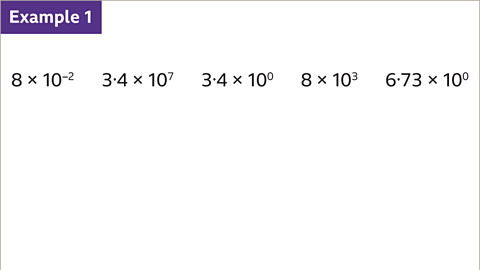 Image caption: Order these values from smallest to greatest.
Image caption: Order these values from smallest to greatest.Understanding Powers of Ten
- When dealing with powers of ten, the magnitude of a number increases as the power of ten increases. For instance, 3 to the power of 4 multiplied by 10 to the power of 7 is the largest number due to its significant power of ten. On the other hand, 8 multiplied by 10 to the power of -2 is the smallest number as it has the least power of ten.
- Another example is 8 multiplied by 10 to the power of 3, which is larger than a number with a power of 10 to the power of 0.
- Comparing numbers with the same order of magnitude, for example, 3 to the power of 4 multiplied by 10 to the power of 0 and 6 to the power of 3 multiplied by 10 to the power of 0, the comparison is done based on the value of the numbers themselves.
- Arranging numbers in ascending order from smallest to greatest helps in better visualization and comparison.
Visual Representation
- Visual aids, like the images provided, can help reinforce understanding of the concept of powers of ten and how they affect numbers.
Illustrative Examples
| Number | Result |
|---|---|
| 3 x 10^5 | 300,000 |
| 3 x 10^4 | 30,000 |
| 3 x 10^0 | 3 |
| 3 x 10^-2 | 0.03 |
Key Takeaway
- Understanding powers of ten is crucial as it directly impacts the numerical value, with higher powers leading to larger numbers.
Direct proportion and the unitary method
- Direct Proportion:
- Direct proportion refers to a relationship between two quantities where they increase or decrease together at a constant rate. For example, if you double one quantity, the other also doubles.
- Unitary Method:
- The unitary method is a technique used to solve problems based on direct proportion. It involves finding the value of one unit and then using it to find the value of a given number of units.
Quiz
- Practice Ordering Numbers in Standard Form:
- Engage in activities that help you become proficient in arranging numbers in standard form.
Real-world maths
Standard form finds applications in various scientific fields:
- Applications in Astrophysics:
- Astrophysicists use standard form to manage large numbers like the speed of light (3 x 10^8 m/s) and distances in space.
- Applications in Chemistry:
- Chemists utilize standard form for values like Avogadro's constant (6 x 10^23) and for measuring tiny distances between particles.

For extreme distances, specialized units like light years and femtometres are used. For instance, a light year is the distance light travels in a year (approximately 9.46 x 10^15 km). On the other hand, a femtometre measures incredibly small distances, such as the nucleus of an atom.
Atomic Structure
- Nucleus: The central positively charged part of an atom or ion, comprising protons and neutrons.
- Extreme Distances: For vast distances, specialized units are utilized such as light-years. A light-year equals the distance light travels in one year, approximately 9 x 10^15 kilometers. Another unit is a femtometer, measuring 1 x 10^-15 meters, which is the approximate length of a quark, a subatomic particle.
 Image caption
Image caption


















