How to calculate speed, distance and time - Year 7 PDF Download

Key points

• Speed:

  A measure of how quickly an object travels a certain distance over a period of time. It is calculated by dividing the total distance traveled by the time taken to travel that distance. Speed is typically measured in units of length per time, such as kilometers per hour or meters per second. It is a compound measure that involves both distance and time, linking the two aspects together.

  For instance, if a car travels 300 kilometers in 5 hours, the speed would be 60 kilometers per hour. This indicates how fast the car is moving on average.

• Constant speed:

  Refers to a steady speed that does not change over time. An example of constant speed is the speed of light, which remains the same. However, in reality, most objects do not move at a constant speed. For instance, the speed of a car can vary due to traffic conditions, road conditions, or driver behavior.

• Units of speed:

  Speed is always expressed as a unit of length per unit of time. Different situations may call for different units of length and time for measurement. This variability in units makes it easier to interpret and compare speed measurements. For example, the speed of a cricket ball may be measured in meters per second (m/s), while a car's speed may be measured in miles per hour (mph).

• Formula triangle:

  A helpful tool used to determine the appropriate calculation needed to solve problems related to speed, distance, or time. If you know two out of the three variables - speed, distance, or time - you can use the formula triangle to find the missing variable. This tool simplifies problem-solving in scenarios where one variable needs to be calculated based on the others.

Speed

• Speed is a measure of how quickly an object changes its position with time. It is calculated as the total distance traveled divided by the time taken to cover that distance. The units of speed are typically expressed as length per unit time, such as kilometers per hour or meters per second.
• Speed gives us information about how fast an object is moving. Most objects do not maintain a constant speed, so we often refer to the average speed over a given period. For instance, the speed of light is a constant speed, while the speed of a car can vary.

Compound Measure

• A compound measure consists of multiple components. For example, speed is a compound measure because it involves both distance and time. By combining these two elements, we can determine how fast an object is moving.

Understanding Speed and Constant

• Constant: A constant is a number or quantity that does not change. For instance, the speed of light remains the same. On the contrary, the speed of a car fluctuates.
• Units of Speed: Speed units always combine a length unit with a time unit. For example, meters per second (m/s) or miles per hour (mph) are commonly used.

Choosing Speed Units

• Varying Units: Depending on the context, different length and time units are selected to enhance readability. For instance, the speed of a cricket ball may be measured in meters per second (m/s), while a car's speed might be in miles per hour (mph).

Understanding Speed, Distance, and Time Relationships

• If you know two out of the three variables - speed, distance, or time - you can calculate the third. Utilizing a formula triangle can assist in determining which calculation is necessary to solve for speed, distance, or time.
• The formula triangle serves as a tool to guide the calculation needed to determine speed, distance, or time in a problem scenario.

Importance of Formula Triangle

• The formula triangle is a visual aid that simplifies the process of solving speed, distance, or time problems.
• It streamlines the decision-making process on the calculation required to find the unknown variable among speed, distance, or time.

Let's illustrate this concept with an example:

Imagine a scenario where a car travels at a speed of 60 miles per hour. If it travels for 3 hours, what distance will it cover?

Using the formula triangle, we can determine that we need to calculate distance. Plugging in the values:

Distance = Speed x Time

Distance = 60 mph x 3 hours

Distance = 180 miles

Therefore, the car will cover a distance of 180 miles in 3 hours at a speed of 60 mph.

Remember, the formula triangle is a valuable tool in solving such problems efficiently.

Video

Watch the video to listen to Steph, a sports coach, explain the practical applications of calculating speed, distance, and time in coaching and playing football.

What is speed and the units of speed?

Speed is a measurement that indicates how fast an object moves. It is a compound measure derived from both distance and time, expressed as a distance covered within a specific unit of time.

• Speed combines distance and time to show how fast an object is moving.
• It is calculated as the distance traveled per unit of time, such as meters per second (m/s) or kilometers per hour (km/h).
• For instance, if a car covers 100 kilometers in 2 hours, its speed can be calculated as 50 km/h.
• Speed is crucial in various fields like sports, physics, and everyday activities to understand motion and performance.

Distances and Units of Measurement

• Distances are measurements of length and can be expressed in metric or imperial units.
• Metric units, part of the metric system, include meter, centimeter, millimeter, and kilometer.
• Imperial units, such as inch, foot, yard, and mile, have largely been replaced by metric units.

Examples of Metric Units

• A length can be measured in meters, centimeters, millimeters, or kilometers.
• For instance, a distance may be 45 meters or 2 kilometers long.

Examples of Imperial Units

• Imperial units include inches, feet, yards, and miles.
• Previously common, these units are now mostly supplanted by metric measurements.

Time Units

• Time units consist of hours, minutes, and seconds.

• Speed is a measure of how fast an object moves in a certain amount of time. For instance, it can be described as 70 miles per hour or 45 meters per second.
• Image caption: Speed is calculated as the distance traveled divided by the time taken.
• Image caption: Different units are used to express speed, such as miles per hour (mph), kilometers per hour (km/h), and meters per second (m/s).
• Image caption: Distance represents the length between two points and can be measured in units like kilometers, meters, centimeters, or miles.
• Image caption: Time is quantified in units like seconds, minutes, and hours.

Examples

Speed is a fundamental concept in physics, determining how quickly an object covers a certain distance over a specific period of time. For instance, a car traveling at 60 miles per hour covers a distance of 60 miles in one hour. Similarly, an athlete running at 6 meters per second covers 6 meters in one second.

When we consider speed in everyday scenarios, think about how fast a car is moving on the highway or how quickly a person is walking to catch a bus. Speed is crucial in understanding motion and is a key concept in physics and mathematics.

Understanding Speed

• Definition of Speed: Speed is the rate at which an object covers distance over time.
• Formula for Speed: Speed = Distance / Time
• Example 1: A car traveling 46 miles in one hour has an average speed of 46 miles per hour (46 mph).

• Example 2: An athlete completing 100 meters in 10 seconds has an average speed of 10 meters per second (m/s).

Key Concepts about Speed

• Speed Calculation: Speed is determined by dividing the distance traveled by an object by the time taken to cover that distance.
• Units of Speed: Speed can be measured in various units such as miles per hour (mph) or meters per second (m/s).

Understanding Speed as a Compound Measure

• Speed as a Compound Measure: Speed combines the concepts of distance and time to provide a comprehensive understanding of how fast an object is moving.
• Example: When we talk about a car's speed, we are essentially discussing how much distance it can cover in a specific amount of time.

How to use a formula triangle to find speed, distance or time

To calculate distance, speed or time given the other two variables:

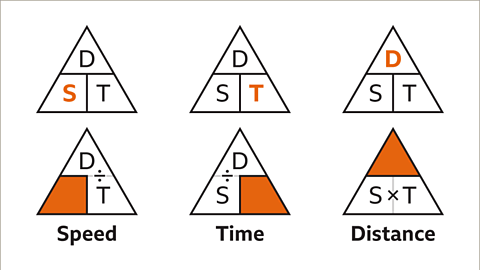
• Draw a formula triangle: A tool to help determine which calculation is needed to find speed, distance, or time. The triangle consists of D for distance, T for time, and S for speed. You start at the top and move clockwise to enter the respective variables.
• Utilize the formula triangle to identify the correct calculation by covering up the variable that needs to be determined. For instance, to find speed, cover the S. To calculate distance, cover the D. To determine the time, cover the T.

Working Out Speed, Distance, and Time

When solving for speed, cover the S. When finding distance, cover the D. When determining time, cover the T.

• To calculate speed, cover the S.
• To calculate distance, cover the D.
• To calculate time, cover the T.

Calculating Variables

The remaining variables in the equations represent:

• For speed: D divided by T (distance divided by time).
• For distance: S multiplied by T (speed multiplied by time).
• For time: D divided by S (distance divided by speed).

Examples

When two variables are provided, the third can be determined using the formula triangle.

Understanding Average Speed

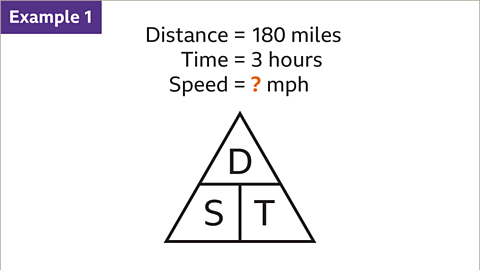
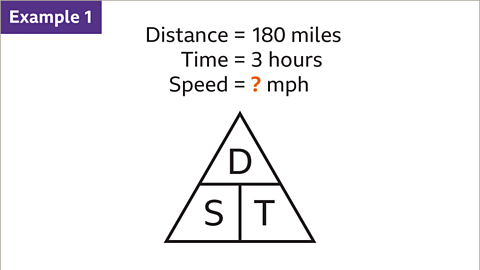
• Calculation of Average Speed

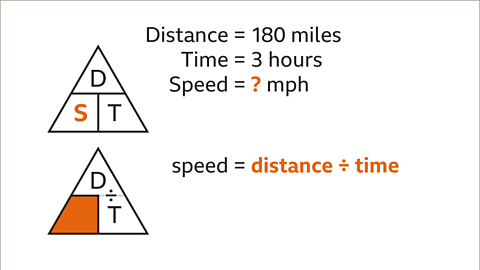
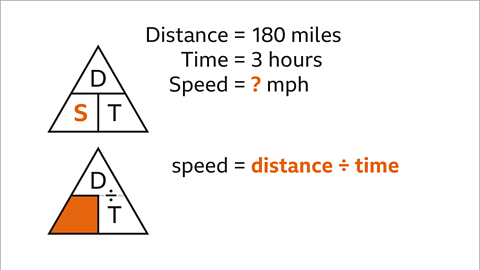
  A car traveling 180 miles in 3 hours requires finding its average speed. This can be determined by dividing the distance covered by the time taken. The formula for average speed is Speed = Distance / Time.

• Application of the Formula

  Let's consider a scenario where a car journey covers 180 miles in 3 hours. By substituting the given values of distance (180) and time (3) into the formula, we find that the average speed of the car is 60 miles per hour.

• Visual Representation

  The formula triangle method provides a structured way to solve average speed problems. By understanding the relationships between distance, time, and speed, one can easily calculate the average speed of a moving object.

• Real-life Example

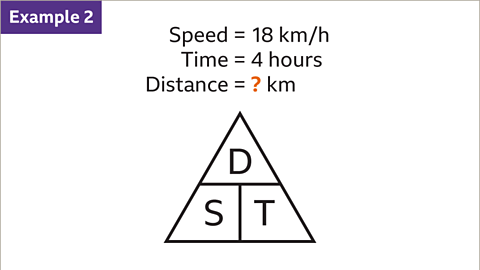
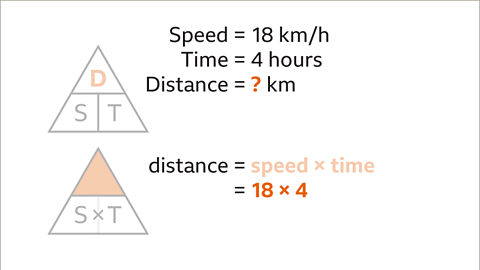
  Imagine a cyclist maintaining an average speed of 18 km/h for 4 hours. To determine the total distance covered, one can apply the average speed formula by dividing the distance traveled by the time taken.

Understanding Distance, Speed, and Time

When it comes to calculating distance, speed, and time, there are fundamental relationships to keep in mind. Let's delve into the details:

Calculating Distance

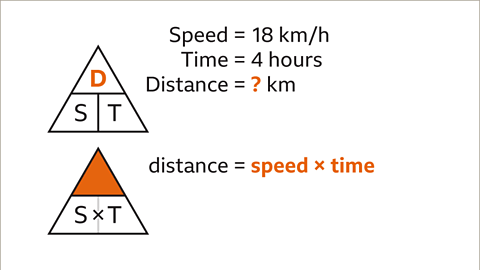
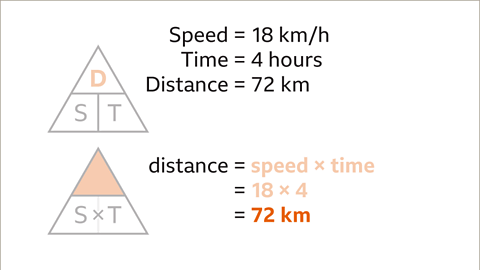
• Image caption: To determine distance, cover up 'D'. The remaining variables are 'S' next to 'T', indicating that distance is calculated by multiplying speed and time.

• Image caption: Substitute the given values for speed (18) and time (4).

• Image caption: Process the calculation (18 × 4) to find the distance cycled, which is 72 km.

• Practise calculating speed, distance and time

  Practice calculating speed, distance, and time in this quiz.

• Real-world maths

  

  Image caption.

  In the early days of space exploration calculations were completed by 'human computers', such as Katherine Johnson.

  This work included calculating speed, distance, and time. Today, as then, these calculations are very important to plan and execute successful and safe space flights.

  The actual calculations are more complex and are only one part of the complicated maths involved.

• Game - Divided Islands