Division in a given ratio - Year 7 PDF Download

Key Points

• Division in a Given Ratio

  Division in a given ratio, also known as sharing in a given ratio, involves a part-to-part comparison.

  • Explanation:

    When dividing an amount in a ratio or finding a fraction of an amount, similar processes are applied.

    • Example:

      If you have $100 to divide in a ratio of 2:3, you would share $40 in the 2-part and $60 in the 3-part.

• Link Between Ratios and Fractions

  Understanding the link between ratios and fractions is crucial for mathematical proficiency.

  • Importance:

    Knowing how ratios and fractions relate helps in various mathematical calculations.

• Using Bar Models for Division in a Given Ratio

  Bar models, which are rectangular bars representing information, aid in understanding numerical methods.

  • Application:

    Bar models can be employed to illustrate the division in a given ratio effectively.

Bar Model

• Bar model: Represents information using one or more rectangular bars. Helps in understanding numerical methods.
• Bar model: Utilized to support comprehension of data.

Link between Ratios and Fractions

• Understanding the relationship between ratios and fractions is a crucial skill to develop.

Image

Back to top

Understanding the Relationship between Ratios and Fractions

Examples

• Ratios: A Simplified Comparison
• Linking Ratios to Fractions
• Ratios Depict Parts of a Whole
• The Denominator in Fractions
• The Numerator in Fractions

Ratios: A Simplified Comparison

To comprehend the connection between a ratio and a fraction, it's vital to grasp the following:

• Ratios: A Comparative View
• Ratios: Breaking Down the Whole
• The Denominator: Understanding Equal Parts
• The Numerator: Counting the Parts Used

Ratios: A Comparative View

Ratios: Breaking Down the Whole

The Denominator: Understanding Equal Parts

The Numerator: Counting the Parts Used

Clear all your Year 7 doubts with EduRev Join for Free

Join for Free

Understanding Fractions

The numerator is the number written at the top of a fraction. It represents the number of parts used out of the whole. For example, in the fraction 1/3, the numerator is 1.

Image Gallery

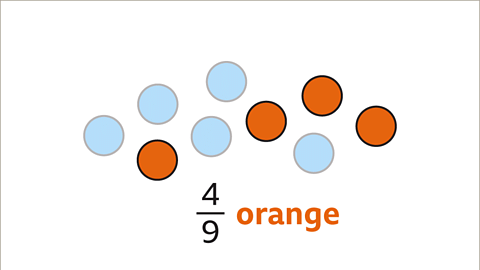
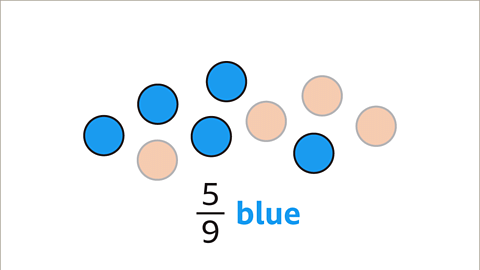
• Image caption: There are nine circles. 4 circles are orange and 5 circles are blue. Find the fraction of orange circles, the fraction of blue circles, and the ratio of orange to blue circles.

• Image caption: 4 out of the 9 circles are orange. The fraction of orange circles is 4/9.
• Image caption: 5 out of the 9 circles are blue. The fraction of blue circles is 5/9.

Understanding Ratios and Fractions

When dealing with ratios and fractions, it is important to grasp the relationship between different parts of a whole. Let's delve into the concepts with clarity and practical examples.

Ratio of Orange to Blue Circles

• The ratio of orange circles to blue circles is 4:5, meaning there are 4 orange circles for every 5 blue circles.
• Illustration: In a scenario with 9 circles (4 orange and 5 blue), the ratio holds true.

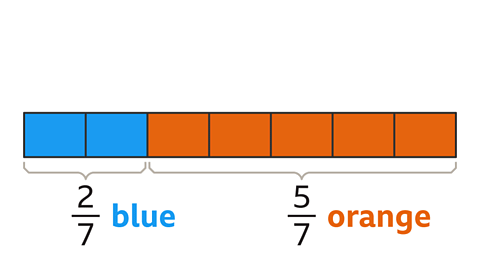
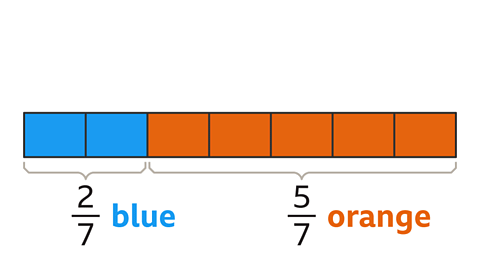
Fractions and Ratios in Bar Representation

• Understanding fractions of colored bars involves discerning proportions visually.
• For example, in a bar divided into 7 parts (2 blue and 5 orange), the fractions are 2/7 for blue and 5/7 for orange.

Comparing Orange and Blue Parts

• The ratio of orange to blue parts is 5:2, indicating there are 5 orange parts for every 2 blue parts.
• Example: Consider a scenario with 7 parts (5 orange and 2 blue) to understand the ratio clearly.

Analyzing Bar Segments for Fractions and Ratios

• When a bar is divided into segments of different colors, determining fractions and ratios becomes crucial.
• For instance, in a bar split into 4 blocks (1 blue and 3 orange), the fractions and ratios can be calculated accordingly.

Understanding Ratios and Fractions

Image caption, 1 of the 4 parts is blue. ¼ of the shape is blue. There is 1 blue part for every 3 orange parts. The ratio of blue to orange parts is 1 : 3

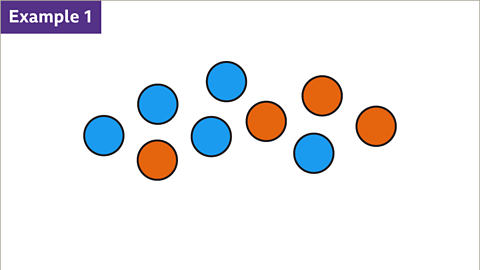
Slide 1 of 9, Example 1

• There are nine circles. 4 circles are orange and 5 circles are blue.
• Find the fraction of orange circles, the fraction of blue circles, and the ratio of orange to blue circles.

Question

Back to top

Key Points

• In a given shape, the ratio of blue to orange parts is 1 : 3.
• When 1 out of 4 parts is blue, this represents a quarter of the whole shape.
• Understanding ratios is crucial to comparing quantities in different proportions.
• Examining circles shaded blue and orange helps visualize fractions and ratios in examples.

Using bar models to divide in a given ratio

• When dividing in a given ratio, we utilize bar models, which are representations using one or more rectangular bars to convey information.
• To start, draw a bar model to depict the whole and divide it into the total number of parts required.
• Calculating the value of one part involves dividing the entire amount by the total number of parts determined.

Understanding Ratios and Proportions

In the realm of mathematics, the concept of ratios and proportions plays a pivotal role. Ratios are used to compare quantities relative to each other, while proportions establish equality between two ratios.

Dividing Ratios

• When dividing a ratio, you determine the value of each share by multiplying the number of parts in each share by the value of one part.
• For instance, consider dividing 40 in the ratio 5:3. This implies splitting 40 into 8 equal parts, where each part holds a value of 5.
• To find the value of one part, you divide the total (40) by the number of parts (8), resulting in each part being valued at 5.

Multiplying Ratios

• When multiplying ratios, you calculate each share's value by multiplying the number of parts in each share by the value of one part.
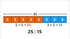
• For example, in a scenario where 40 is divided in the ratio 5:3, the first share amounts to 25 and the second share amounts to 15.

Examples

Let's explore these concepts through visual representations:

Image	Description
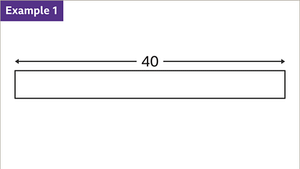	Illustration: The bar represents the whole. Divide 40 in the ratio 5:3.
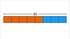	Visual: The whole (40) is divided into 8 equal parts based on the ratio 5:3.
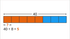	Visual Aid: Calculation of the value of one part.
	Visual Example: Multiplying the number of parts in each share by the value of one part.

Understanding Money Sharing in Ratios

When individuals split money in a given ratio, it's crucial to comprehend how to distribute the amount effectively.

Calculating Individual Shares

• Tariq and Annie divide £90 in the ratio 2:3.
• To determine the value of one part, divide the total amount (£90) by the number of parts (5). Hence, one part equals £18.
• By multiplying the number of parts each person receives by the value of one part, you can find their individual shares. Tariq receives £36, and Annie receives £54.

Illustrative Example

Image caption: Tariq and Annie share £90 in the ratio 2:3.	Image caption: Draw bars to represent the parts Tariq and Annie receive.

Download the notes Division in a given ratio

Download as PDF

Download as PDF

How to divide in a given ratio – numerical method

To divide an amount in a given ratio A part-to-part comparison:

• Sum (verb): To add up the parts of the ratio to get the total number of parts.
• Find the value of one part by dividing the amount by the total number of parts.
• Find the value of each share in the ratio by multiplying the number of parts in each share by the value of one part.

Multiplying Ratios

When we talk about multiplying ratios, we are essentially dealing with dividing a quantity into parts according to a specific ratio. Let's dive into this concept with some examples:

Examples

• Image caption: Divide 600 in the ratio 4 : 3 : 5

• Image caption: Sum the parts of the ratio. 4 + 3 + 5 = 12

• Image caption: To find the value of one part, divide the amount (600) by the total number of parts (12). 600 ÷ 12 = 50. The value of one part is 50

• Image caption: To find the value of each share, multiply the number of parts of each share (4, 3, and 5) by the value of one part (50). 600 shared in the ratio 4 : 3 : 5 is 200 : 150 : 250

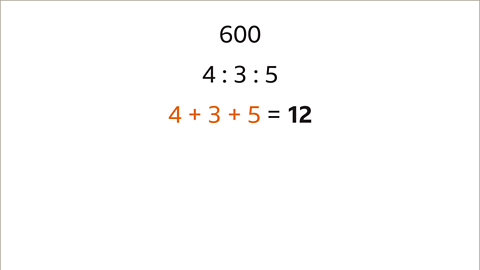
Sharing in Ratios

• Image caption: Dai, Jim, and Kate share £300 in the ratio 8 : 5 : 2. How much money do they each receive?

• Image caption: Sum the parts of the ratio (8, 5, and 2) to get the total number of parts. 8 + 5 + 2 = 15. The total number of parts is 15

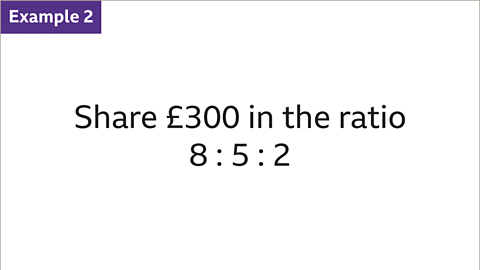
Understanding Ratios and Proportions

• When determining the value of one part in a ratio, you divide the total amount by the total number of parts. For instance, if there are 300 units in total and the ratio consists of 15 parts, each part is valued at 20.
• Calculating individual shares in a ratio involves multiplying each share by the value of one part. For example, if the ratio shares are 8, 5, and 2, and the value of one part is 20, the resulting shares would be 160, 100, and 40 respectively.
• In a scenario where Dai, Jim, and Kate share £300 in the ratio 8:5:2, Dai would receive £160, Jim £100, and Kate £40. This illustrates how ratios distribute amounts among different shares.

Take a Practice Test Test yourself on topics from Year 7 exam

Practice Now

Practice Now

Practice Example: Dividing an Amount in a Given Ratio

• Consider an instance where you need to divide 600 units in the ratio 4:3:5. This situation involves splitting the total amount according to the specified ratios.

Question

Back to top

Practise division in a given ratio

• Quiz

Practise division in a given ratio in this quiz. You may need a pen and paper to complete these questions.

Real-world maths

• Video

Ratios are frequently utilized in professions where liquids must be combined in precise proportions.

Observe the video to understand how a hairdresser must mix a hair color dye solution and a developer in a particular ratio to achieve a specific shade safely. The ratio may vary based on the products being mixed.

A 200 ml blend of color and developer is needed for a customer. The required shade employs color and developer in the ratio 2:3.

200 ml is split in the ratio 2:3.

The hairdresser should combine 80 ml of color and 120 ml of developer.

• Game - Divided Islands