Inverse proportion - Year 7 PDF Download

Key Points

• If two quantities are inversely proportional, as one increases, the other decreases at the same rate. For instance, having more workers on a job can reduce the time taken to complete the task, showcasing inverse proportionality.
• Inverse proportion signifies that two variables multiply to yield a fixed product. When one variable doubles, the other one halves. This concept is denoted using the proportional symbol (𝝏).
• An example of inverse proportion is when the number of chocolate bars (b) is directly proportional to their cost (C), represented as b 𝝏 C. If two variables A and B are inversely proportional, this can be written as A 𝝏 B.
• Replacing the proportionality symbol (𝝏) with an equals sign (=) in an equation implies a direct relationship. The constant value relates to the quantities increasing or decreasing at the same rate.
• To solve inverse proportion problems, the constant of proportionality, the fixed value of the product of two inversely proportional variables, is utilized. For example, if two people work for 9 hours and three people work for 6 hours, both scenarios result in a total of 18 working hours.

Proportional and Inverse Proportion

• When two variables are in inverse proportion, they multiply to give a fixed product. If one variable increases, the other decreases accordingly. This relationship is represented using the proportional symbol (∝).
• For instance, the number of chocolate bars (b) being directly proportional to their cost (C) can be denoted as b ∝ C. If two variables A and B are inversely proportional, it can be written as A ∝ 1/B.

Proportional Symbol

• When the proportionality symbol (∝) is replaced with an equals sign (=) in an equation, it signifies a direct proportionality. The constant value in the equation relates to the quantities that increase or decrease at the same rate.

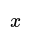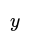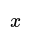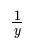Inverse Proportion Problems

• Inverse proportion problems involve the use of the constant of proportionality, a fixed value representing the product of two inversely proportional variables.
• To illustrate, consider two people working for 9 hours and three people working for 6 hours. The total work hours remain the same: (2 x 9 = 18) and (3 x 6 = 18). This fixed product is a characteristic of inversely proportional variables.
• To find the missing quantity, divide the constant of proportionality by the known quantity.

Example

• For instance, if two people can paint a house in 12 hours and three people can paint the same house in 8 hours, the constant of proportionality is 6 (2 x 12 = 3 x 8 = 6).
• If we know that four people are working, we can find out how long it will take by dividing the constant of proportionality (6) by the number of people (4), which equals 1.5 hours.

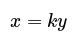
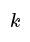
How to decide whether two variables are inversely proportional

To determine if two variables are inversely proportional, consider the following criteria:

• When one quantity increases, the other decreases in the same proportion.
• When one quantity decreases, the other increases in the same proportion.
• The quantities exhibit a fixed product, known as the constant of proportionality.

Let's break down these points further:

1. Inverse Proportionality with Increasing and Decreasing Quantities

• As one variable rises, the other falls at an equivalent rate. For instance, if the number of workers increases, the time taken to complete a task decreases proportionally.

2. Inverse Proportionality with Fixed Product

• Consider two scenarios: when two people work for 9 hours and when three people work for 6 hours. The total work hours remain constant at 18 in both cases due to the fixed product of inversely proportional variables.

Product

• The product is the outcome of multiplying one number by another. For instance, if we multiply 4 by 5, the product is 20 (4 x 5 = 20).
• It represents the result of a multiplication operation between two or more numbers.

Constant of Proportionality

• The constant of proportionality is a fixed value that arises from the product of two inversely proportional variables.
• For example, consider two scenarios: two people working for 9 hours and three people working for 6 hours. In this case, the total work hours remain the same (2 x 9 = 18 and 3 x 6 = 18), indicating a constant of proportionality.
• It serves as a factor that maintains the relationship between inversely proportional quantities.

Explanation of Inverse Proportionality in Rectangles

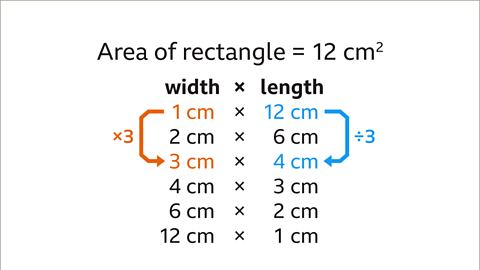
• When the area of a rectangle is fixed at 12 cm², the width and length of the rectangle are inversely proportional to each other.
• For instance, if the width of the rectangle is multiplied by 3, the length is divided by 3 to maintain the fixed area of 12 cm².
• This inverse relationship holds true for all instances where the width and length of rectangles have a constant area.

Understanding Inverse Proportionality

• Two quantities are said to be inversely proportional when one quantity increases, and the other decreases in the same proportion.
• For rectangles with a fixed area of 12 cm², this means that as one dimension grows, the other shrinks by the same factor to maintain the area constant.

Illustrative Examples

• Image caption: Explain why the width and length of rectangles with a fixed area of 12 cm² are inversely proportional.

• Image caption: Two quantities are inversely proportional when one quantity increases and the other quantity decreases in the same proportion. This is true for all the widths and lengths of a fixed area of 12 cm². For example, as the width is multiplied by 3, the length is divided by 3. The width and length of rectangles with a fixed area are inversely proportional.

• Image caption: Two quantities are inversely proportional if the quantities have a fixed product. The table shows that the width multiplied by the length is always 12 cm². The width and length of rectangles with a fixed area are inversely proportional. The fixed area (12cm²) is the constant of proportionality.

Understanding Inverse Proportion in Rectangles

When exploring the relationship between the width and length of rectangles with a fixed perimeter of 12 cm, it becomes evident that they are not inversely proportional. Let's delve into the reasons behind this phenomenon.

Width and Length Dynamics

• Image caption: An equation can be written connecting the width and the length.

Consider the scenario where the width and length are both crucial factors in determining the shape of a rectangle. Here, the width and length interact in a unique manner.

• Image caption: Explain why the width and length of rectangles with a fixed perimeter of 12 cm are not inversely proportional.

Contrary to what one might assume, the width and length of rectangles with a fixed perimeter of 12 cm do not exhibit an inverse relationship. For instance, when the width increases from 1 cm to 2 cm, the length does not decrease in a directly proportional manner.

• Image caption: Two quantities are inversely proportional when one quantity increases and the other quantity decreases in the same proportion. This is not true for all the widths and lengths of a fixed perimeter of 12 cm.

It's important to note that the concept of inverse proportionality does not apply uniformly to all widths and lengths of rectangles with a fixed perimeter. For example, when the width doubles, the corresponding change in length does not follow a proportional decrease pattern.

• Image caption: Two quantities are inversely proportional if the quantities have a fixed product.

For values to be inversely proportional, their product must remain constant. However, in the case of the width and length of rectangles with a fixed perimeter, this condition is not met, indicating a deviation from inverse proportionality.

Slide 1 of 7, Example 1: Area of Rectangle and Inverse Proportionality

• When the area of a rectangle is fixed at 12 cm², the width and length are inversely proportional.
• For a rectangle with an area of 12 cm², if the width increases, the length decreases proportionally to maintain the fixed area.
• This relationship is because the product of the width and length must equal the fixed area of 12 cm².
• Examples:
  • If the width is 1 cm, the length would be 12 cm (1 * 12 = 12).
  • If the width is 2 cm, the length would be 6 cm (2 * 6 = 12).
  • If the width is 3 cm, the length would be 4 cm (3 * 4 = 12).
  • If the width is 6 cm, the length would be 2 cm (6 * 2 = 12).
  • If the width is 12 cm, the length would be 1 cm (12 * 1 = 12).

Question

Explain why the width and length of rectangles with a fixed area of 12 cm² are inversely proportional.

Solving inverse proportion problems using multiplicative reasoning

multiplicative reasoning involves using multiplication and division to find other values. To use this method:

• Look for multiplicative links: Identify a multiplication relationship (number of times greater) or a division relationship (number of times smaller).

Repeat the Multiplication or Division

• When you perform a multiplication or division operation on one variable, ensure you apply the same operation to the other variable as well. This principle holds true for quantities that can vary across a range of values.

Examples

• Consider a scenario where the number of builders and the time they take to construct houses exhibit an inverse relationship. For instance, if it takes 15 builders 12 months to build houses, how long would it take 5 builders to accomplish the same task?

• Another illustration involves the correlation between the number of builders and the time taken to construct houses. This relationship is such that as the number of builders decreases, the time required for construction increases. For instance, if the number of builders is reduced by a factor of three (15 ÷ 3 = 5), the corresponding time is multiplied by three (12 x 3 = 36). Therefore, it would take 5 builders approximately 36 months (3 years) to complete the construction.

Understanding Inverse Proportions

When two quantities are inversely proportional, as one quantity increases, the other decreases, and vice versa. This relationship is characterized by a constant product between the two quantities.

Example 1: Speed and Time

• As speed increases, the time taken for a journey decreases.
• Given an average speed of 30 mph, the journey takes 4½ hours.
• To complete the journey in 2¼ hours, the necessary speed would be 60 mph.

Example 2: Builders and Time

• The number of builders and the time taken to build houses are inversely proportional.
• If 15 builders take 12 months to build the houses, 5 builders would take less time.

• Question

• Back to top

• Solving inverse proportion problems: constant of proportionality

• inverse proportion: Two variables multiply to give a fixed product. When one variable doubles, the other halves.

• inverse proportion problems can be solved by using the constant of proportionality. This constant represents the fixed value of the product of two inversely proportional variables.

• For example, if two people work for 9 hours and three people work for 6 hours, they will work the same total number of hours. This is because 2 x 9 = 18 and 3 x 6 = 18, indicating the fixed product for each pair of variables.

• Constant of proportionality method:

• When two variables are inversely proportional, their product remains constant. If one variable doubles, the other variable halves.
• To solve inverse proportion problems, we utilize the constant of proportionality. This constant signifies the unchanging value of the product of two variables that are inversely related.
• For instance, consider a scenario where two people work for 9 hours and three people work for 6 hours. Despite the difference in the number of people and hours worked, the total work done is the same. This equality is maintained by the constant of proportionality.

Constant of Proportionality

Examples

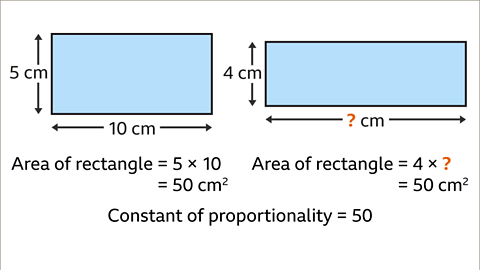
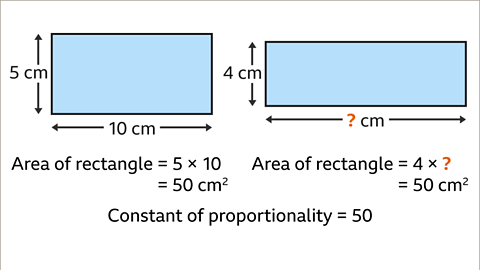
Proportionality in Mathematics

• Understanding Proportional Relationships
  • When two quantities are inversely proportional, they change in opposite directions.
  • For instance, if one quantity increases, the other decreases, and vice versa.
• Finding Missing Lengths
  • Given a constant of proportionality (50) and a known quantity (4), divide to find the missing length:
  • Divide 50 by 4 to get 12.5, which represents the missing length in centimeters.
• Calculating Worker Requirements
  • Consider a scenario where the number of workers and completion time are inversely proportional.
  • With 20 workers, a project takes 310 days. To finish in 50 days, the number of workers needed can be calculated.
• Determining the Constant of Proportionality
  • Find the constant by multiplying given quantities (e.g., 20 workers and 310 days).
  • Multiplying 20 by 310 gives 6200, representing the total days needed to complete the job.

Explanation: In the context of mathematics, understanding proportional relationships is crucial. When quantities are inversely proportional, their changes are interdependent. For instance, when finding missing lengths, dividing the constant of proportionality by a known quantity reveals the missing length. In scenarios involving worker requirements, inverse proportionality guides calculations to determine the necessary workforce for specific completion times. Calculating the constant of proportionality empowers us to estimate the total duration required for a project based on given factors.

The Constant of Proportionality

Divide the constant of proportionality (6200) by the known quantity (50) to find the missing quantity. 6200 ÷ 50 = 124. There needs to be 124 workers to complete the project in 50 days.

• Image caption: Divide the constant of proportionality (6200) by the known quantity (50) to find the missing quantity. 6200 ÷ 50 = 124. There needs to be 124 workers to complete the project in 50 days.

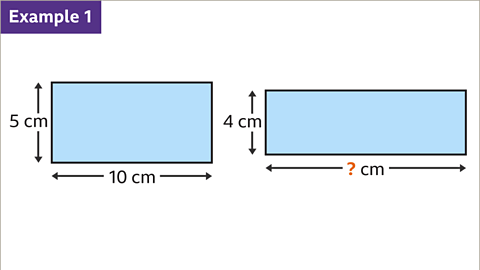
Rectangles and Proportions

Example 1: A diagram showing two rectangles. The rectangles have equal areas. The width and length of rectangles with equal areas are inversely proportional. Find the missing length.

• Slide 1 of 6: Example 1 - A diagram showing two rectangles. The rectangles have equal areas. The width and length of rectangles with equal areas are inversely proportional. Find the missing length.

Question

Practise ratio and inverse proportion

Practise ratio and inverse proportion with this quiz. You may need a pen and paper to help you work things out.

Quiz

Real-world maths

Inverse proportion may be used by a construction company. The more builders, the faster a building project will be completed.

More workers also means more costs, but when a builder has to meet a set deadline they will employ more people to complete the job on time. This is so that they do not have to pay a penalty for completing the job late.

Game - Divided Islands

• Builders increase speed of project completion in inverse proportion.
• More workers mean faster work but also higher costs.
• Meeting deadlines prompts builders to hire more workers to avoid penalties.