Year 7 Exam > Year 7 Notes > How to draw direct and inverse proportion graphs
How to draw direct and inverse proportion graphs - Year 7 PDF Download
| Table of contents |

|
| Introduction |

|
| How to Recognize Whether Graphs Show Direct or Inverse Proportion |

|
| How to Create a Direct Proportion Graph with Real-Life Data |

|
| How to draw a graph for inverse proportion |

|
Introduction
- Direct proportion is where variables change in the same direction and by the same proportion. As one variable increases or decreases, so does the other at the same rate. For example, if one variable is multiplied by 10, the other is also multiplied by 10, and if one is halved, the other is also halved. The ratio x/y remains constant.
- The notation and general equation for y being directly proportional to x is y ∝ x.
- A graph of direct proportion is a straight line passing through the origin (0, 0). When x = 0, y = 0.
- Inverse proportion graphs use the notation and equation
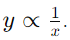 The product of the two variables, x and y, remains constant. For example, if x = 20 and y = 4, then x × y = 20 × 4 = 80. If x = 20, then y = 1.
The product of the two variables, x and y, remains constant. For example, if x = 20 and y = 4, then x × y = 20 × 4 = 80. If x = 20, then y = 1. - A graph showing inverse proportion is a curve that approaches the axes as x and y reach extreme values. As one variable increases, the other decreases at the same rate. For example, if one variable is multiplied by 10, the other is divided by 10, and if one is halved, the other is doubled.
- Graphs are plotted using pairs of values, called coordinates. A direct proportional graph can be drawn by plotting three points, while an inverse proportional graph needs more points for an accurate curve.
How to Recognize Whether Graphs Show Direct or Inverse Proportion
- If a graph demonstrates direct proportion:
- The graph appears as a straight line.
- The line passes through the origin (0, 0).
- For any coordinate (x, y), the ratio x : y remains constant.
- The equation of the line follows the general form y = nx.
- If a graph illustrates inverse proportion:
- The graph forms a curve.
- The curve does not intersect either axis.
- For any coordinate (x,y), the product of x and y remains constant (xy = k).
- The equation of the curve follows the general form y = k/x for each coordinate.
Example
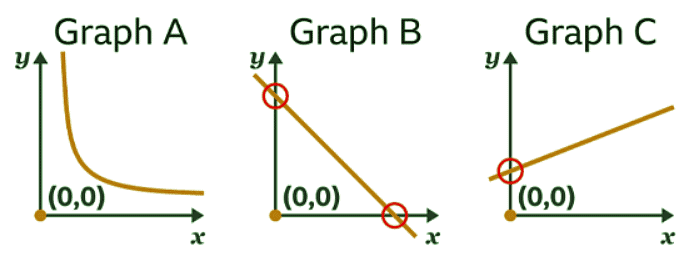
Example: Explain why none of these graphs shows direct proportion.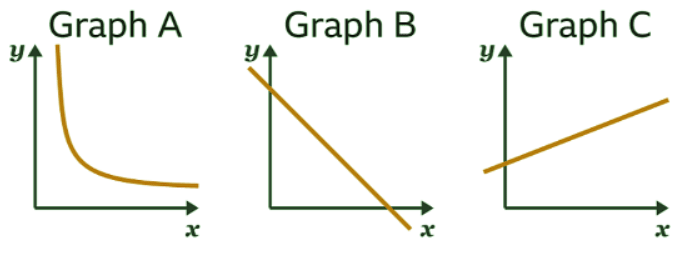 Sol: A graph shows direct proportion when the graph is a straight line, and the line goes through the origin (0, 0).
Sol: A graph shows direct proportion when the graph is a straight line, and the line goes through the origin (0, 0).
- Graph A is not a straight line, so does not show direct proportion.
- Graph B is a straight line, however the line does not pass through the origin (0, 0), so the graph does not show direct proportion.
- Graph C is a straight line, however the line does not pass through the origin (0, 0), so the graph does not show direct proportion.
How to Create a Direct Proportion Graph with Real-Life Data
To sketch a direct proportion graph:
- Identify the relationship between the variables (x:y).
- Create a table of values using this ratio. Start with (0, 0) and use the given ratio to determine additional points. You need at least three coordinates for plotting.
- The initial point is always (0, 0).
- Another point repeats the specified ratio.
- Multiply to derive at least one more coordinate.
- At least three coordinates are necessary, although more can be included.
- Plot the identified coordinates.
- Draw a straight line passing through these points and the origin (0, 0).
Example
Example: Given that 5 miles are approximately 8 kilometres, draw a graph of distance in miles (𝒙) against distance in kilometres (𝒚) to show the directly proportional relationship.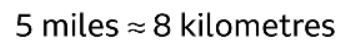 Sol:
Sol: 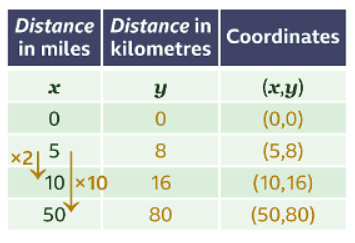
- The distance in miles and the distance in kilometres are directly proportional. The ratio of miles : kilometres is always 5 : 8. A distance of zero in miles is zero in kilometres. This gives the point (0, 0). The given fact that 5 miles ≈ 8 kilometres gives the point (5, 8). These values can be multiplied to give other coordinates. For example, doubling the coordinate (5, 8) gives (10, 16). Multiplying the coordinate (5, 8) by ten gives (50, 80).
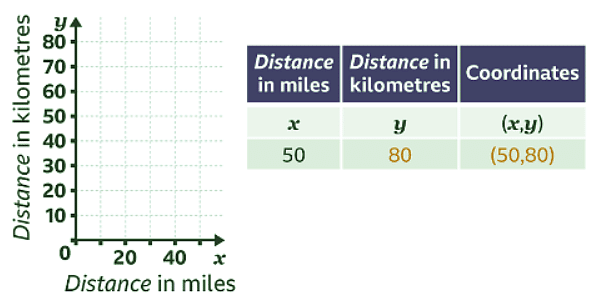
- The greatest number of miles is 50 miles. The 𝒙-axis (horizontal axis) should go up to 50. The greatest number of kilometres is 80. The 𝒚-axis (vertical axis) should go up to 80
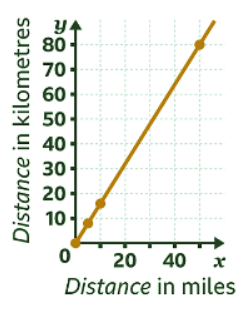
- The points are plotted. The points are all in a straight line. Join the points to complete the graph. Values may be read from the graph when converting between miles and kilometres.
How to draw a graph for inverse proportion
To draw a graph for inverse proportion:
- Identify the constant product of the variables (x): When dealing with inverse proportion, it's crucial to first recognize the constant product of the variables involved. This product remains the same even as the values of the variables change.
- Draw a table of values and find factor pairs: Creating a table of values is essential to visualize the relationship between the variables in inverse proportion. Factor pairs are pairs of numbers that, when multiplied, result in the same product. By identifying these pairs, you can accurately represent the inverse proportion on a graph.
- Each factor pair yields the same product.
- Since the graph is a curve, multiple coordinates are necessary.
- It is essential to plot these coordinates accurately.
- When graphing a rectangle with a fixed area, it is essential to draw a smooth curve through the points.
Example
Example: A rectangle has a fixed area of 24 cm². Draw the graph of the length of the rectangle (𝒙) against its width (𝒚). Sol:
Sol: 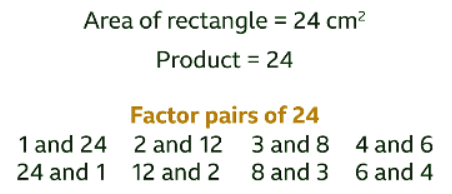
- The area of the rectangle is 24 cm². The product of the length and the width is always 24. List the factor pairs of the product (24) to generate the coordinates. Each factor pair will be used twice.
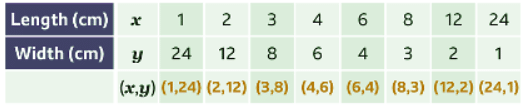
- Draw a table of values. Use the factor pairs of the product (24) to generate the coordinates. Several coordinates are needed because the graph is a curve.
- The largest factor of 24 is 24. The 𝒙- and 𝒚-axes go up to 24
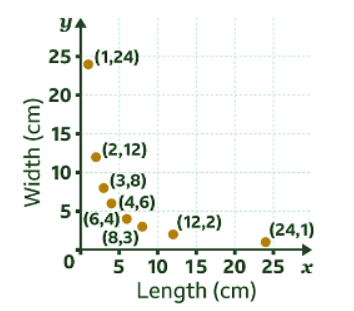
- Plot the coordinates.

- Draw a smooth curve through the plotted points.
Related Searches


















