Solving for x - 3 - Year 7 PDF Download
Key Points
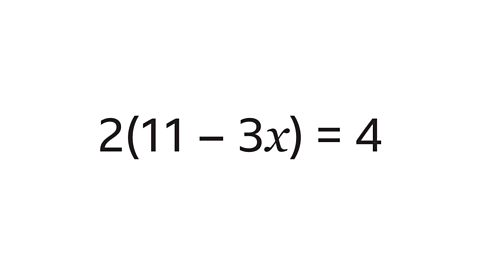 Image caption
Image caption- An understanding of expanding brackets is crucial when solving equations containing brackets.
- An equation is a mathematical statement demonstrating the equality of two expressions, akin to a balanced scale.
Expanding Brackets
- Expanding brackets simplifies equations, making them easier to solve without altering the expression's value.
- It involves multiplying to remove brackets and maintaining balance in the equation by applying operations to both sides equally.
Equations and Balancing
- In equations, both sides of the equals symbol must retain the same value to stay balanced.
- Terms in equations are elements separated by addition or subtraction signs, linked by the equals symbol.
Note: Understanding these fundamental concepts is pivotal for mastering algebraic manipulation and problem-solving in mathematics.
Mathematical Concepts
Equation
- A mathematical statement demonstrates equality between two expressions using the symbol =.
- For example, in the equation 2x + 3 = 9, both sides must be equal.
Term
- An element within an algebraic sentence separated by + or - signs.
- In the expression 5x - 2y, "5x" and "-2y" are terms.
Keeping Equations Balanced
- To maintain balance in an equation, the same operation must be performed on both sides.
- For instance, in the equation 4x = 12, to solve for x, divide both sides by 4.
Expanding Brackets
- Expanding brackets involves multiplying to remove the brackets from equations, simplifying them in the process.
- Expanding brackets does not alter the value of an expression; it merely represents the same mathematical idea in different forms.
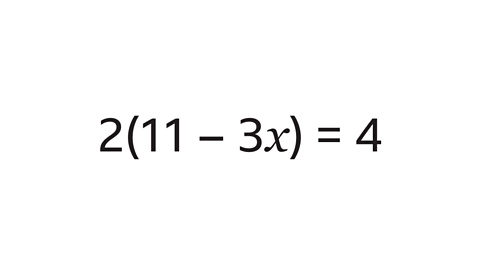 Image captionBack to top
Image captionBack to topSolving equations with brackets
Some equations involve brackets. When solving such equations, the initial step is to expand the brackets.
expand- When you multiply an expression within brackets, ensure that everything inside the bracket is multiplied by the term (or number) outside the bracket.
- Expand the brackets to create an equivalent equation.
Expanding brackets is vital for simplifying and solving equations. Let's explore this concept further with an example:
Example:
Consider the equation: 3(x + 2) = 9
To solve this equation, the first step is to expand the brackets:
- 3(x + 2) becomes 3x + 6
Now, the equation becomes 3x + 6 = 9. By further solving this simplified equation, you can find the value of x.
Expanding brackets is a fundamental algebraic concept that enables you to solve complex equations by breaking them down into simpler forms.
Equivalent
- When something is described as equivalent, it means that it is the same as something else but presented in a different form.
Simplify (Equation)
- An equation can be simplified to make it easier to solve. This process often involves combining like terms and expanding brackets to isolate the desired term.
Divide both sides by the coefficient
- To find the value of a variable in an equation, you can divide both sides by the coefficient of that variable. This step helps in isolating the variable and solving for its value.
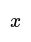 |
Complex Equation Simplification Example
Example
Image gallery
Skip image gallery
Steps to Solve the Equation
- Image caption: Solve the equation 3(x - 5) = 18
- Image caption: Expand the brackets on the left-hand side of the equation. 3x - 15 = 18
- Image caption: Subtract 15 from both sides. The equation simplifies to 3x = 3
- Image caption: Divide both sides by 3. The equation shows that x = 1
- Image caption: It is important to check the answer. Substitute the value of 1 for x in the equation. 3(1 - 5) = 18
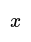
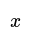
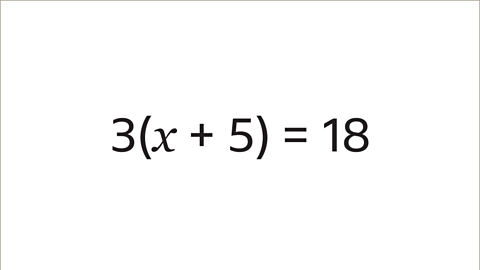
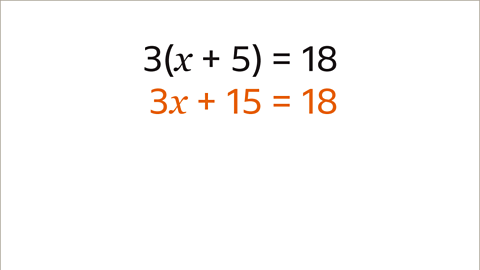
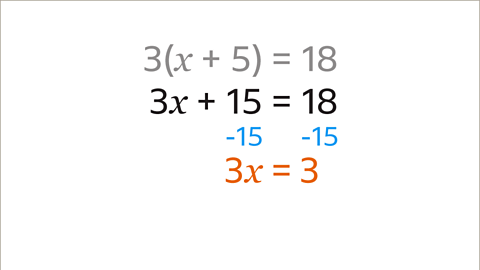
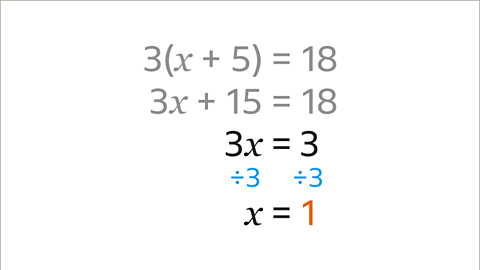
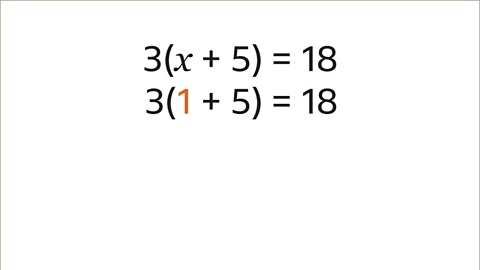
Image Caption
- The solution is 𝑥 = 1. When 𝑥 is 1 then the value inside the brackets is 6. Multiply the value outside the brackets (3) with the value inside the brackets, 3 x 6 = 18. This confirms that the solution of 𝑥 = 1 is correct.
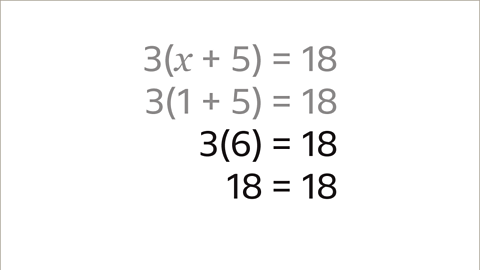
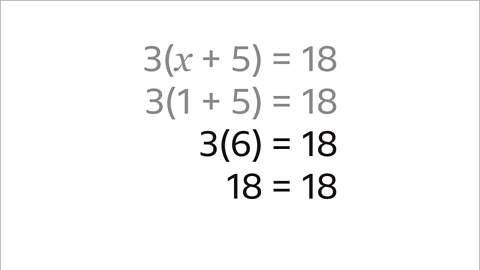
Slide 1 of 6
- The equation: three open bracket x plus five close bracket equals eighteen. Solve the equation 3(x - 5) = 18
Question
Back to top
Solving equations where the coefficient of x is negative
When we work with equations containing negative coefficients of x, a specific approach is needed to simplify and solve them effectively.
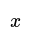
- Begin by expanding the brackets, paying close attention when negatives are involved.
- Rearrange the equation so that the coefficient of the unknown variable becomes positive.
- Manipulation is crucial here, where we adjust the equation strategically to make the coefficient positive.
- Simplify the equation further to isolate the term with the unknown variable.
Solving Equations with Variables
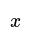
- Divide by the coefficient to find the solution.
- Check your solution by substituting your answer into the equation.
Example
When solving equations with variables, it is important to follow these steps:
- Start by dividing by the coefficient to find the solution.
- Verify your solution by substituting it back into the original equation.
Image Gallery
In the image gallery below, we have the following steps illustrated:
- Image caption: Solve the equation 2(11 – 3𝑥) = 4
- Image caption: Expand the brackets on the left-hand side of the equation
- Image caption: Adjust the coefficient of the variable to maintain balance
- Image caption: Isolate the variable term by performing the necessary operations
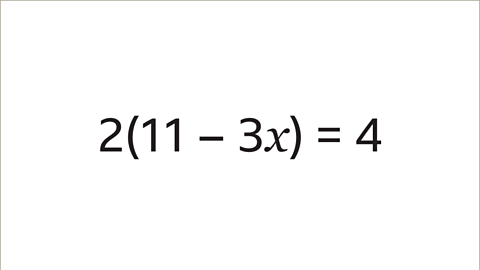 | 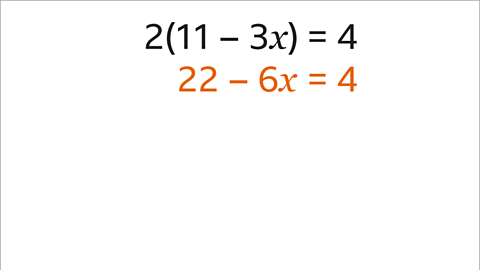 |
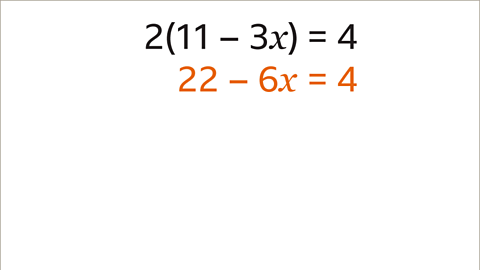 | 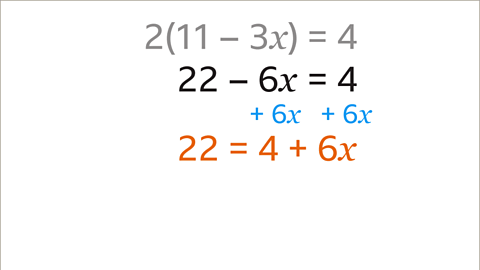 |
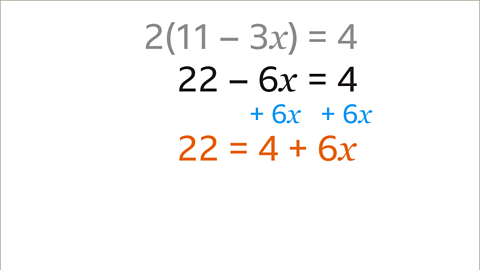 | 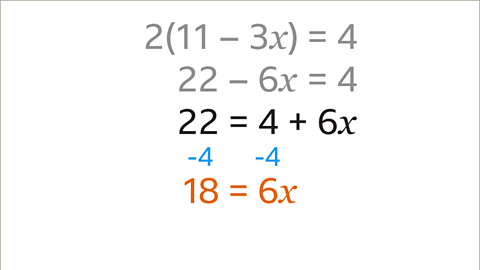 |
Throughout this process, we ensure that every step is carefully executed to solve the given equation effectively.
Understanding Equations with Variables
Equations with variables are fundamental in mathematics. Let's delve into the process of solving them step by step.
Solving Equations with a Variable
- Given an equation like \(2(11 - 3x) = 4\), where \(x\) is a variable, the first step is to simplify the expression.
- Substitute the known value of the variable into the equation. For instance, if \(x = 3\), replace \(x\) with 3 in the equation.
- By substituting the value of 3 for \(x\), we can solve the equation step by step to find the value of the variable.
Step-by-Step Equation Solution
- For the equation \(2(11 - 3 \times 3) = 4\), start by calculating what is within the brackets.
- After simplifying the expression within the brackets, the equation becomes more manageable to solve.
- Multiply the values both inside and outside the brackets to find the final solution of the equation.
Verification of the Solution
- Once you have found a value for the variable that satisfies the equation, it's crucial to verify the solution.
- Check by substituting the solution back into the original equation to ensure it holds true.
| Slide | Equation | Description |
|---|---|---|
| 1 of 7 | Two open brackets eleven subtract three x close bracket equals four | Solve the equation \(2(11 - 3x) = 4\) |
Practise solving equations with brackets
- When solving equations with brackets, it's essential to follow the order of operations.
- Brackets help prioritize which operations to perform first in a mathematical expression.
Quiz
- A quiz on equations with brackets can help reinforce your understanding of this concept.
- For effective practice, have a pen and paper ready to solve the problems.
Real-life maths
- In real-life scenarios, pharmacists use equations with brackets to calculate medication doses.
- For instance, Young's formula helps calculate the correct dose for a child based on the adult dose.
A pharmacist may need to calculate the dose for an eight-year-old child when the adult dose is 200 mg:
Child's dose = Adult's dose × ( )If 'd' represents the child's dose, then:
d = 200 × ( )
d = 200 × ( )
d = 200 × 0.4
d = 80
The correct dose for the eight-year-old child would be 80 mg.
Game - Divided Islands
- The game "Divided Islands" involves strategic thinking and decision-making.
- Players must navigate challenges to unite divided territories and achieve a common goal.



















