Solving for x - 3 - Year 7 PDF Download
Key Points
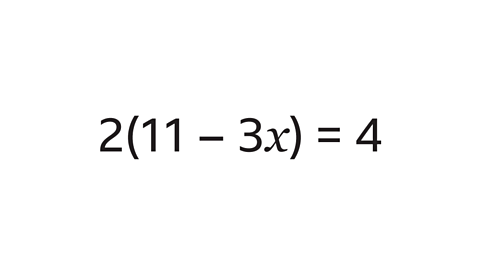 Image caption
Image caption- An understanding of expanding brackets is crucial for solving equations that contain brackets.
- An equation is a mathematical statement demonstrating equality between two expressions. It's akin to a balanced scale where both sides of the equals symbol (=) hold the same value.
Expanding Brackets
When we talk about expanding brackets in mathematics, we are essentially multiplying to eliminate the brackets. This process simplifies equations and makes them easier to solve. Importantly, expanding brackets does not alter the value of an expression; it just represents the same mathematical concept in a different form.
Equations in Balance
Equations are like balanced scales where both sides of the equals sign hold equivalent values. To maintain this balance, any operation performed on one side must also be done on the other. Some equations involve brackets, and expanding these brackets simplifies the equation without changing its fundamental value.
Equation
- The concept of an equation is a fundamental mathematical statement indicating equality between two expressions, connected by the symbol "=".
- In an equation, both sides must remain balanced. This means that any operation performed on one side should also be carried out on the other to maintain equality.
Example:
Consider the equation: 2x + 3 = 7. To solve this equation, we aim to find the value of x that satisfies the equality. By subtracting 3 from both sides, we get 2x = 4. Finally, dividing by 2 gives us x = 2.
Term
- A term in algebra represents an element within an algebraic expression. Terms are separated by addition or subtraction signs.
- When simplifying or solving algebraic equations, it's crucial to understand and manipulate individual terms.
Example:
In the expression 4x^2 + 3y - 2, the terms are 4x^2, 3y, and -2. Each of these components is considered a separate term.
Expanding Brackets
- Expanding brackets involves removing the brackets by multiplying the terms inside. Expanding makes the equation simpler to solve by eliminating the brackets.Expanding makes the equation simpler to solve by eliminating the brackets.Expanding makes the equation simpler to solve by eliminating the brackets.Expanding makes the equation simpler to solve by eliminating the brackets.Expanding makes the equation simpler to solve by eliminating the brackets.ExpandingExpandingRemoving brackets simplifies the equation.
- Expanding brackets does not alter the value of an expression; it just represents it differently. An expression is a mathematical sentence composed of terms, expressed numerically or symbolically.An expression is a mathematical sentence composed of terms, expressed numerically or symbolically.An expression is a mathematical sentence composed of terms, expressed numerically or symbolically.An expression is a mathematical sentence composed of terms, expressed numerically or symbolically.An expression is a mathematical sentence composed of terms, expressed numerically or symbolically.An expressionAn expressionAn expression is a mathematical sentence composed of terms.
Image Caption
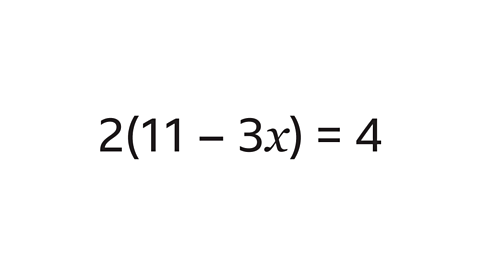
Solving equations with brackets
Some equations involve brackets. When dealing with equations containing brackets, the initial step is to expand these brackets.
Key Concepts:- When you multiply an expression within brackets, ensure that everything inside the bracket is multiplied by the term (or number) outside the bracket.
- Expanding the brackets results in an equivalent equation.
Let's dive deeper into the process of solving equations with brackets with some illustrative examples:
Expanding Brackets Example:
Consider the equation: 2(x + 3) = 10.
To solve this, we expand the bracket: 2x + 6 = 10.
Now, we can proceed with solving the equation further.
Another Example:
Let's work with a more complex equation involving brackets: 3(2x - 5) = 21.
By expanding the brackets, we get: 6x - 15 = 21.
This paves the way for finding the solution to the equation step by step.
Understanding how to expand brackets is fundamental in solving equations efficiently.
Understanding Equations Simplification
- Equivalent: The concept of equivalence signifies being the same but in a different form.
- Simplify (Equation): When we simplify an equation, we make it easier to solve by techniques like combining like terms and expanding brackets. The goal is to isolate the 'x' term.
- Divide both sides by the coefficient of 'x': This step allows us to find the value of 'x' by dividing both sides of the equation by the coefficient of 'x'.
Explanation with Examples:
- Simplify (Equation): For instance, if we have the equation 2x + 3 = 7, we can simplify it by subtracting 3 from both sides to isolate the x term, resulting in 2x = 4.
- Divide both sides by the coefficient of 'x': Consider the equation 3x = 12. By dividing both sides by 3 (the coefficient of x), we find that x = 4.
Explanation of Solving a Linear Equation
Example
- Image gallerySkip image gallery
- Image caption: Solve the equation 3(x + 5) = 18
- Image caption: Expand the brackets on the left hand side of the equation. x multiplied by 3 is 3x. 5 multiplied by 3 is 15. The 18 is outside the bracket so remains as 18. The equation is now 3x + 15 = 18
- Image caption: Subtract 15 from both sides. The equation is simplified to 3x = 3. The x term has now been isolated.
- Image caption: x multiplied by 3 is 3. Divide both sides by the 3 (the coefficient of x). The equation shows that x = 1
- Image caption: It is important to check the answer. The original equation stated that 3(x + 5) = 18. Substitute the value of 1 in place of the x term.
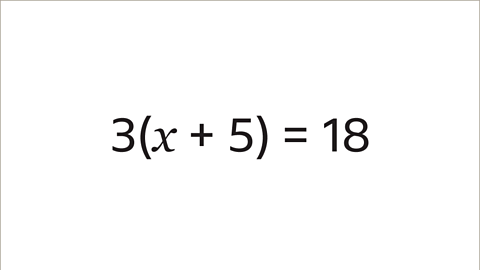
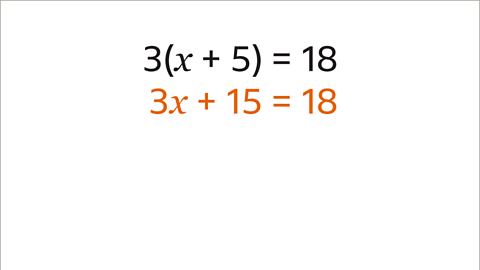
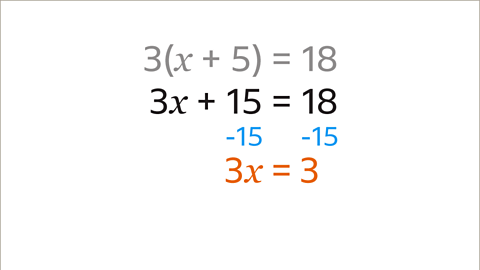
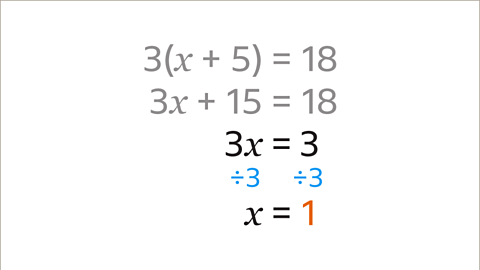
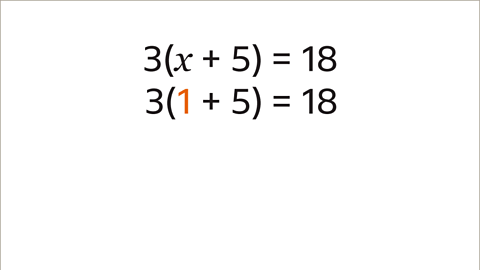
Image caption
- The given solution is 𝑥 = 1. When 𝑥 is 1, the value inside the brackets is 6. By multiplying the value outside the brackets (3) with the value inside the brackets, 3 x 6 = 18. This calculation confirms that the solution of 𝑥 = 1 is accurate.
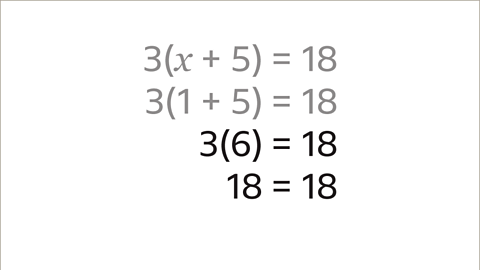
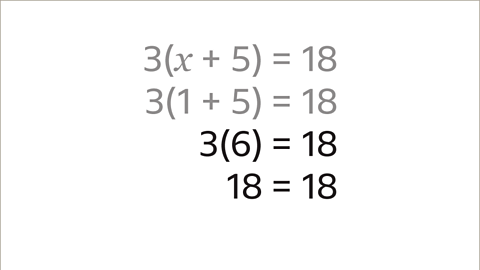
Slide 1 of 6
- The equation given is: three open bracket x plus five close bracket equals eighteen. To solve this equation, we have 3(x - 5) = 18.
Question
- Back to top
Solving equations where the coefficient of \(x\) is negative
- When we encounter equations with negative coefficients of \(x\), the process involves expanding brackets while being cautious of the negative values present.
- To proceed, we need to manipulate the equation to ensure that the coefficient of the unknown term, \(x\), becomes positive. This manipulation is crucial for simplifying the equation effectively.
- The next step is to simplify the equation further, aiming to isolate the term containing \(x\). This simplification stage helps in clearly identifying the value of \(x\).
Equation Solving Process
Example
Image gallery Skip image gallery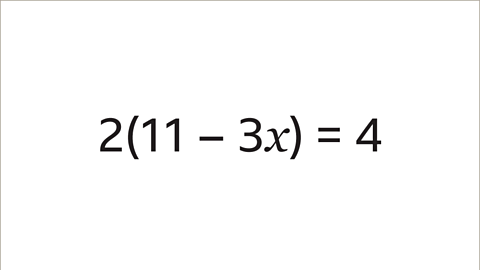
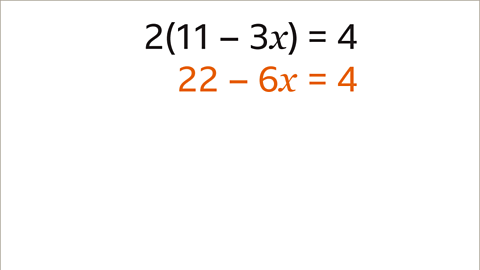

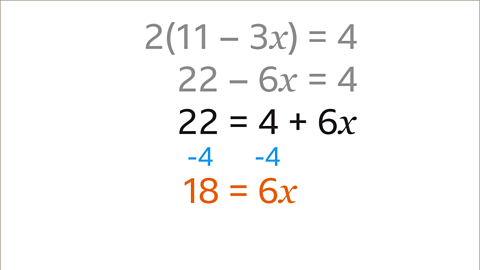
Understanding Equations with Variables
Equations with variables are fundamental in mathematics. They represent relationships between unknown values and constants.
The Role of Coefficients in Equations
- Coefficients Influence Variables: Coefficients are the numbers that multiply variables in equations.
- Importance of Coefficients: They determine how the variable affects the overall equation.
Solving Equations Step by Step
- Solving for a Variable: To find the value of a variable, we manipulate the equation using inverse operations.
- Illustrative Example: Given the equation 2(11 - 3x) = 4, let's solve for x.
Understanding the Equation 2(11 - 3x) = 4
- Step 1: Distribute the 2 to both terms inside the parentheses.
- Step 2: Solve for x by isolating it on one side of the equation.
Applying the Solution
- Verification: Always verify the obtained value by substituting it back into the original equation.
- Example Calculation: For x = 3, the equation simplifies to 2(11 - 3*3) = 4.
Conclusion
Equations with variables involve systematic steps to find unknown values. By understanding coefficients and following a structured approach, we can effectively solve such equations.
| Slide Number | Equation to Solve | Description |
|---|---|---|
| Slide 1 of 7 | The equation: two open bracket eleven subtract three x close bracket equals four. | Solve the equation 2(11 - 3x) = 4 |
| Slide 1 of 7 | The equation: two open bracket eleven subtract three x close bracket equals four. | Solve the equation 2(11 - 3x) = 4 |
Question
Back to topPractise solving equations with brackets
Quiz
Practise solving equations with brackets with this quiz. You may need a pen and paper to help you with your answers.
Back to topReal-life maths
A pharmacist might use an equation involving brackets to calculate the correct amount of medicine needed for a patient according to their age.
If a pharmacist needed to work out the correct dose for an eight-year-old child, when the adult dose is 200 mg, they can use ‘Young’s formula’ to help them:
Child’s dose = Adult’s dose × ( \(\frac{age}{age + 12}\) ) Image caption
Image captionIf \(x\) represents the child’s dose, then:
\(x\) = 200 × ( \(\frac{8}{8 + 12}\) )
\(x\) = 200 × ( \(\frac{8}{20}\) )
\(x\) = 200 × 0.4
\(x\) = 80
The correct dose for the eight-year-child would be 80 mg.
 Image captionBack to top
Image captionBack to topGame - Divided Islands
Back to topParaphrased Content
- A pharmacist may utilize an equation with brackets to determine the precise medication quantity required based on a patient's age.
- For instance, when computing the accurate dosage for an eight-year-old child, considering the adult dose as 200 mg, the pharmacist can employ 'Young's formula'.
- The formula for the child's dose is calculated as the adult's dose multiplied by the fraction \(\frac{age}{age + 12}\).
- If we denote the child's dose as \(x\), the computation unfolds as \(x\) = 200 × \(\frac{8}{8 + 12}\).
- This simplifies to \(x\) = 200 × \(\frac{8}{20}\), resulting in \(x\) = 200 × 0.4, which equals 80 mg, representing the correct dosage for the eight-year-old child.



















