Solving for x - 4 - Year 7 PDF Download
| Table of contents |

|
| Key points |

|
| Equations involving one fraction |

|
| Example |

|
| Equations with fractions on both sides |

|
| Understanding Equations with Fractions |

|
| Question |

|
| Practise solving equations using fractions |

|
Key points
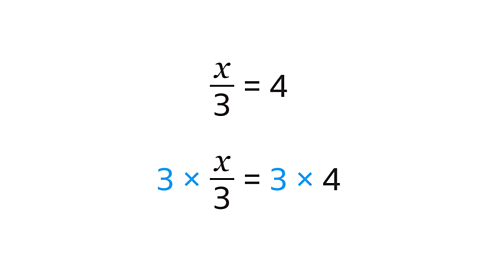 Image caption
Image caption- An equation is a mathematical statement showing that two expressions are equal. The expressions are linked with the symbol =, similar to a set of scales in balance.
- The terms on either side of the equals sign (=) have the same value as each other. Solving equations becomes simpler when the number of terms is reduced.
- Equations must remain in balance. Any operation performed on one side of the equation must also be done to the other side, such as multiplying or dividing by the same value.
- It's important to understand that 'is the same as' is equivalent to '=', and 'is the same as' is equivalent to '='.
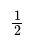
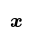
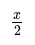
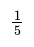
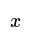
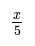
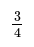
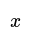
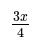
Additional Points:
- Solving equations becomes easier when the number of terms is reduced.
- Equations need to stay in balance. Whatever is done to one side of the equation must also be done to the other. For example, multiplying or dividing each side of the equation by the same value.
- It is useful to know that 'is the same as' and 'is the same as', whereas 'is the same as'.
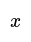
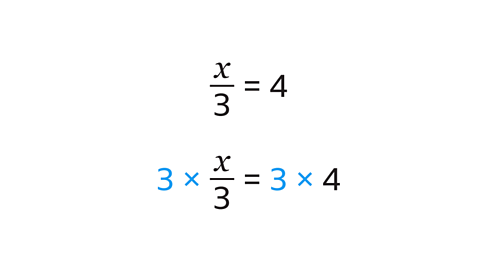 Image captionBack to top
Image captionBack to topEquations involving one fraction
- When an equation contains a single fraction, a common initial step is to multiply both sides by the denominator, which is the number at the bottom of the fraction. For instance, in the fraction 1/3, the denominator is 3. This action eliminates the fraction from the equation, reducing the number of terms and resulting in a new balanced equation with only one unknown variable.
- Multiplying both sides of the equation by the denominator removes the fraction entirely.
- This process reduces the number of terms, ensuring that the resulting equation remains balanced.
- The new equation will contain just one unknown variable, which simplifies the process of solving the equation.
- It is recommended to verify the solution by substituting it back into the original equation, a practice commonly known in algebra as substitution.
Example
Image gallery
Skip image gallery
- Image caption, Solve the equation ⅓x = 4 by finding the value of x.
- Image caption, ⅓x = 4 can be expressed as x/3 = 4.
- Image caption, Multiply both sides of the equation by 3 to maintain equality.
- Image caption, After multiplication by 3 on both sides, the result is x = 12.
- Image caption, To verify, substitute 12 for x in the equation x/3 = 4.
- Image caption, If x = 12, then 12 ÷ 3 = 4. This confirms x = 12 as the solution.
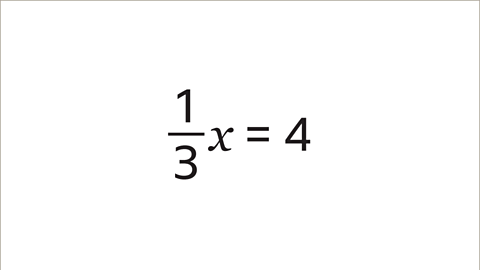
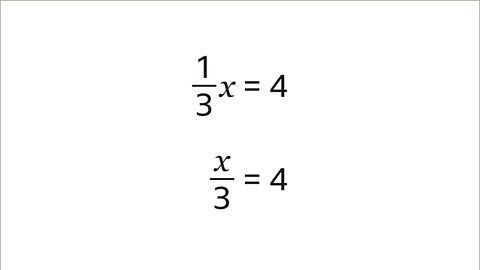
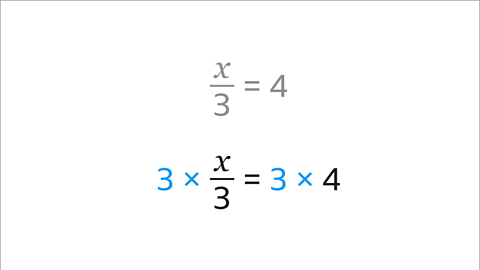
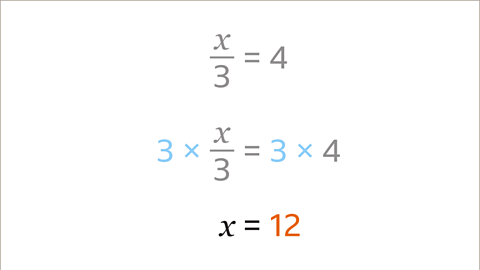
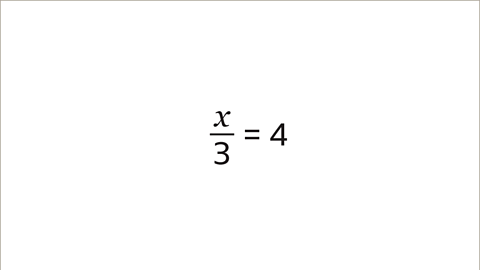
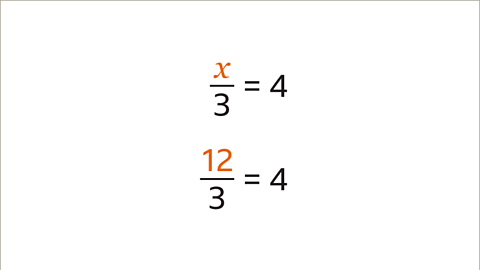
Equations with fractions on both sides
Equations involving fractions on both sides need to be simplified by multiplying both sides by an appropriate number to keep the equation balanced.
Find the lowest common multiple (LCM)
The lowest multiple that is common to two or more numbers. The LCM of 15 and 12 is 60 because it is the lowest value in both of their multiplication tables. Also known as the least common multiple.
- Explanation of LCM
- Illustrative example: Finding the LCM of 15 and 12
Multiply both sides of the equation by the lowest common multiple
This action will reduce the number of terms and lead to a new equation that remains balanced.
- Importance of multiplying by LCM
- Example demonstrating the process of multiplying both sides by LCM
Understanding Equations with Fractions
When dealing with equations that involve fractions, there are specific steps to follow in order to simplify and solve them effectively.
Image Gallery
- Image caption: Solve the equation by working out the value of x.
- Image caption: Both sides of the equation involve a fraction. Find the lowest common multiple (LCM) of the denominators (4 and 2).
- Image caption: The lowest common multiple (LCM) is 4. Multiply both sides by 4.
- Image caption: The fraction element of the equation has now been removed. This leaves a new equation that is still in balance.
- Image caption: Expand the brackets.
- Image caption: Subtract x from both sides of the equation, x + 3 - x = 3 and 2x - 2 - x = x - 2.
- Image caption: Add 2 to both sides of the equation. 3 + 2 = 5 and x - 2 + 2 = x. The answer is x = 5.
When faced with equations containing fractions, understanding how to find the lowest common multiple (LCM) and performing operations to simplify the equation is crucial. Let's break down the process with examples:
Example: Solving an Equation with Fractions
Consider the equation: \( \frac{x+3}{4} = \frac{x-1}{2} \)
We aim to solve for the value of x in this equation.
Finding the Lowest Common Multiple (LCM)
Both sides involve fractions with denominators 4 and 2. The LCM of 4 and 2 is 4.
Multiplying by the LCM
To eliminate the fractions, we multiply both sides by 4:
\( 4 \times \frac{x+3}{4} = 4 \times \frac{x-1}{2} \)
\( x+3 = 2(x-1) \)
Further Simplification
We can now expand the brackets to continue simplifying the equation.
After simplifying the equation further by performing arithmetic operations, we arrive at the final solution: \( x = 5 \).
By following these steps systematically, we can successfully solve equations involving fractions.
Question
Back to top
Solve the equation by working out the value of \( x \).
Explanation
- It is crucial to verify the solution. The given problem initially expressed as \( x + \frac{3}{4} = x - \frac{1}{2} \). To solve this, substitute 5 for the \( x \) terms.
- When \( x = 5 \), then \( (5 + 3) \div 4 = 2 \) and \( (5 - 1) \div 2 = 2 \). Substituting 5, both sides of the equation balance out. This validates the solution \( x = 5 \).
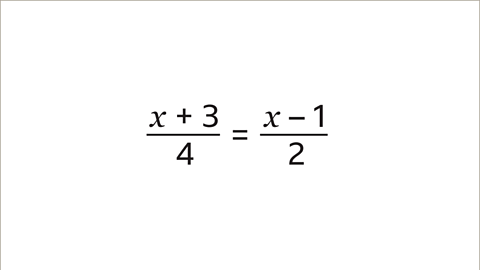
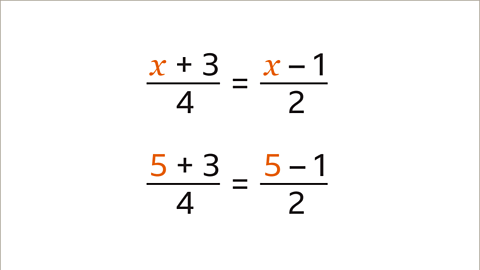
Summary
| Slide | Equation | Task |
|---|---|---|
| 1 of 9 | X plus three over four equals x minus one over two. | Solve the equation by working out the value of \( x \). |
Practise solving equations using fractions
Quiz
Practise solving equations with fractions with this quiz. You may need a pen and paper to help you with your answers.
Back to topGame - Divided Islands
Back to topUnderstanding Fractions in Equations
- Fractions are parts of a whole number, represented as a numerator over a denominator.
- When solving equations with fractions, it's crucial to find a common denominator to add or subtract them.
- For example, in the equation 1/2 + 1/3 = ?, the common denominator would be 6.
Multiplying and Dividing Fractions
- When multiplying fractions, you simply multiply the numerators and denominators together.
- For division, you multiply by the reciprocal of the second fraction.
- For instance, in 1/2 ÷ 1/4, you multiply by 4/1 to get the result.
Example: Solving Equations
- Given the equation 2/3 + 1/6 = ?, find a common denominator and simplify the fractions to solve.
- First, find the common denominator (6) and convert both fractions.
- Then, add the fractions together to get the result.
Practical Application in Divided Islands Game
- In the game "Divided Islands," fractions might be used to distribute resources among different territories.
- Players may need to calculate fractional amounts to ensure fair distribution and strategic decision-making.













