Circumference of a Circle - Year 7 PDF Download
Key points
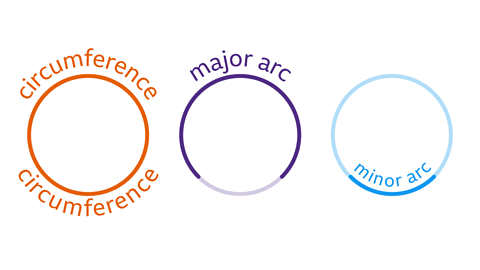 Image caption
Image captionAll circle calculations
- Circumference is the distance around a circle, which is essentially its perimeter.
- When the circumference is divided by the diameter (the distance across the circle through its center), it gives the constant π (pi).
- This relationship holds for all circles because they are mathematically similar.
- The circumference is a length measured in units like centimeters and meters.
Pi and its significance
- Pi (π) is an irrational number, meaning it cannot be expressed exactly, similar to √2.
- An approximate value like 3.142 or 3.14 is commonly used in calculations.
- Modern calculators represent π using the symbol and can provide decimal approximations.
- Rounding numbers in calculations allows for answers with a defined level of accuracy.
Key Concepts in Geometry
- Circumference: The distance around a circle, essentially its perimeter.
- Diameter: The distance across a circle from one circumference, through the center, to the other circumference.
- Pi as an Irrational Number: Pi, represented by the symbol π, is a value that cannot be expressed exactly. It is commonly approximated as 3.142 or 3.14 in calculations. Modern calculators use the symbol π which can be converted to a decimal approximation using the appropriate key.
Explaining Circumference
The circumference of a circle is the total distance around its outer boundary. Imagine a wheel - the length of the outer edge all the way around is its circumference. For example, if a circle has a radius of 5 units, its circumference would be 2πr = 2 x 3.14 x 5 = 31.4 units.
Understanding Diameter
The diameter of a circle is the distance across it, passing through the center. It is essentially the longest chord of the circle. For instance, if a circle has a diameter of 10 units, its radius would be half of that, which is 5 units.
Significance of Pi as an Irrational Number
Pi is a crucial mathematical constant used in various mathematical calculations involving circles and spheres. Its irrational nature implies that it cannot be precisely expressed as a fraction or decimal. For practical purposes, we often approximate it to 3.14 or 3.142.
Key Concepts in Mathematics
- Irrational Number: A value that cannot be expressed exactly, like √2 and π.
- Surd: An irrational number, including square roots that cannot be written as an exact decimal and special values like π.
Rounding Numbers
- The ability to round a number to a number of decimal places or to a number of significant figures allows for answers to be written to an agreed degree of accuracy.
Video
Watch the video to learn how circles and circumference play a crucial role in various fields, including sports like football.
Understanding the Circle and π (Pi)
To grasp the concept of a circle, it's essential to familiarize yourself with specific terms:
- The perimeter of a circle is its total boundary or the distance around the shape.
- An arc is a portion of the circumference. It is termed major when it covers over half of the circle and minor when it covers less than half.
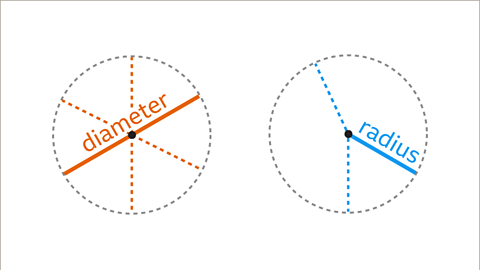
- The diameter represents the full distance across a circle, from one side of the circumference to the other through its center.
- The radius is the distance from the center of the circle to its circumference. Notably, the radius measures half of the diameter.
Let's delve deeper into these concepts:
Perimeter of a Circle
The perimeter refers to the total length around a circular shape. It is calculated by summing the lengths of all sides that form the boundary of the circle.
Arcs in a Circle
Arcs are sections of the circle's circumference. They are classified based on how much of the circumference they cover. For instance, a major arc spans more than half of the circle, while a minor arc covers less than half.
Diameter
The diameter is the longest chord that can be drawn through the center of a circle, connecting two points on the circumference. It essentially represents the width of the circle.
Radius
The radius is the distance from the center of the circle to any point on its circumference. It is half the length of the diameter and crucial in various mathematical calculations involving circles.
Additionally, it's vital to understand the mathematical constant π (pi), which is the ratio of a circle's circumference to its diameter. It is approximately equal to 3.14159 and is a fundamental element in circle-related calculations.
What is π (Pi)?- π (pi) is a mathematical constant representing the ratio of a circle's circumference to its diameter. It is denoted by the Greek symbol π.
- For any circle, dividing the circumference by the diameter yields the value of π.
- π is an irrational number, meaning it cannot be expressed precisely like √2. Therefore, approximations like 3.142 or 3.14 are commonly used in computations.
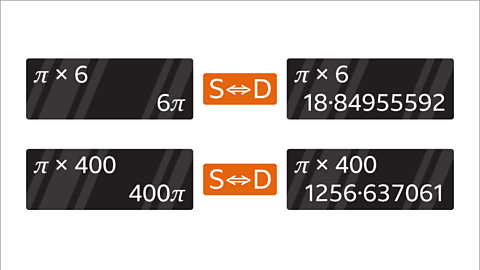
- On calculators, the π button provides greater accuracy, sometimes displaying answers in terms of π. The display format can be changed to a decimal by pressing the S ⟷ D button, and the final result is rounded as per the required accuracy.
- π (pi) is pivotal in geometry, physics, and various other fields due to its fundamental role in determining properties of circles and spheres.
- Understanding π is crucial for calculating the areas and volumes of circular and spherical objects accurately.
Understanding the Vocabulary of Circles
- The final result is adjusted to the requested level of precision, which could be in terms of decimal places or significant figures.
Example
Image gallery Skip image gallery- The vocabulary related to circles comprises terms like circumference, arc, diameter, and radius.
 Image caption,
Image caption, - The circumference of a circle represents the perimeter of the shape. It includes terms like circumference, arc, diameter, and radius.
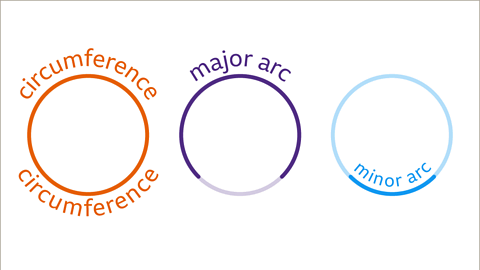 Image caption,
Image caption, - The diameter of a circle is the complete distance across, passing through its center. It is twice the radius, which is the distance from the center to the circumference.
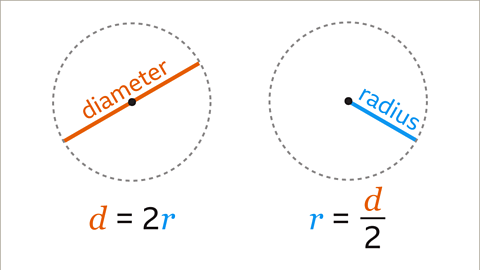 This HTML snippet paraphrases the information provided regarding the vocabulary of circles, including the concepts of circumference, arc, diameter, and radius, with accompanying images and captions for better understanding.
This HTML snippet paraphrases the information provided regarding the vocabulary of circles, including the concepts of circumference, arc, diameter, and radius, with accompanying images and captions for better understanding.Understanding Circle Concepts
- Circle Properties: Circles have fixed diameters and radii regardless of where they are measured on the circle.
- The Value of Pi: Pi (π) is a constant used in circle calculations.
- Pi and Circumference: Pi is the ratio of a circle's circumference to its diameter; it is always the same value.
- Approximations of Pi: In calculations, the approximate value of π is often used, such as 3.14159 or 3.14.
- Calculations with Pi: When using π in calculations on a calculator, the result may be shown in terms of π or as a decimal by toggling the display settings.
Additional Explanations with Examples:
- When calculating the circumference of a circle, you always divide the circumference by the diameter, resulting in the constant value of π.
- For practical purposes, approximations like 3.14 are often used when precise calculations are not necessary.
- On calculators, the π button allows convenient access to this constant for various calculations involving circles.
- Converting π to its decimal equivalent simplifies calculations and makes the results more practical for real-world applications.
 |  |
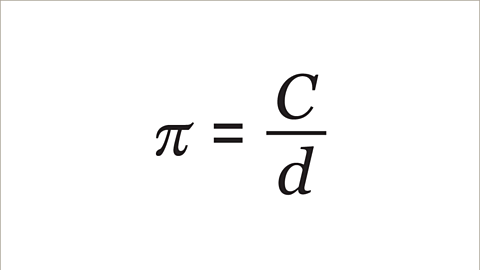 |  |
 |
Accuracy in Calculations
- The final result is adjusted to the requested level of precision in a problem, which could be a specific number of decimal places (dp) or significant figures (sf).
Examples
Vocabulary of the Circle
- The terminology related to circles comprises words such as circumference, arc, radius, and diameter.
Question
- Paraphrase the provided details, explaining thoroughly and supplementing with examples where necessary. Present all information in bullet points structured with appropriate headings. Ensure no topic is overlooked.
Response
- Accuracy in Mathematical Computations:
- Ensuring the precision of the final outcome according to the specified decimal places or significant figures in a given problem is crucial.
- Illustrative Instances:
- For instance, when 18.84955592 is rounded to two decimal places, it becomes 18.85.
- Similarly, when 1256.637061 is rounded to three significant figures, it becomes 1260.
- Vocabulary of Circles:
- The circle-related vocabulary encompasses essential terms like circumference, arc, diameter, and radius.
Calculate the circumference of a circle
- To determine the circumference of a circle, you can use the provided approximation for pi (π) or the pi button on a calculator along with either the diameter or the radius.
- Diameter: It is the distance across the circle, from circumference to circumference, passing through its center.
- Radius: This is the distance from the center of the circle to the circumference.
- The Concept of Circumference:
- When we talk about the circumference of a circle, we are referring to the distance around the circle. It is a fundamental measurement when dealing with circles.
- Calculating Circumference with Diameter:
- One way to calculate the circumference is by using the diameter of the circle. The formula for this is C = πd, where C represents the circumference and d is the diameter.
- Applying the Formula:
- To find the circumference using the diameter, simply substitute the value of the diameter into the formula C = πd. This formula represents a fundamental concept in mathematics and is essential when working with circle measurements.
- Example:
- Let's consider a circle with a diameter of 10 units. By applying the formula C = πd, we can calculate the circumference as follows: C = π * 10 = 31.415 units.
- Calculating Circumference with Radius:
- Alternatively, we can calculate the circumference using the radius of the circle. The formula for this approach is C = 2πr, where C is the circumference and r is the radius.
- Applying the Formula with Radius:
- When finding the circumference using the radius, substitute the value of the radius into the formula C = 2πr. This method provides another way to determine the distance around a circle.
- Example with Radius:
- Suppose we have a circle with a radius of 5 units. By utilizing the formula C = 2πr, we can find the circumference as follows: C = 2 * π * 5 = 31.416 units.
Understanding Circumference of a Circle
- When calculating the circumference of a circle, always round the answer to the degree of accuracy requested in the question. This might mean rounding to a specific number of decimal places or significant figures.
- Utilizing the π button on a calculator automatically provides the answer in terms of π. If calculating manually, the circumference is simply the value of the diameter preceding π.
Examples
- It's important to note that the formula for the circumference of a circle can be based on either the diameter or the radius of the circle.
- For the formula involving the diameter, it is represented as C = πd. This implies multiplying π by the diameter of the circle. In the case of the radius-based formula, it is C = 2πr. This indicates multiplying 2 by π and then by the radius. This process can be done without a calculator by doubling the radius and multiplying by π.
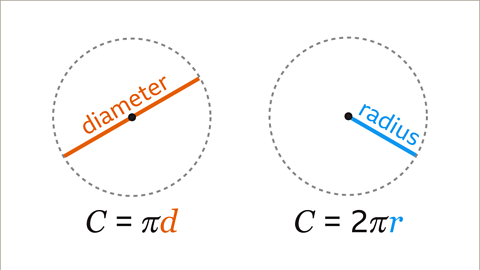 Image caption, The formula for the circumference of a circle uses either the diameter or the radius of the circle. Image caption, The formula for the circumference of a circle uses either the diameter or the radius of the circle. | 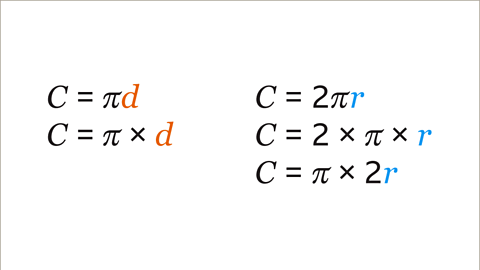 Image caption, The formula using the diameter is 𝒊 = π𝒅. Multiply π by the diameter of the circle. The formula using the radius is 𝒊 = 2π𝒓. This means that 2 is multiplied by π and then multiplied by the radius. This may be worked out without a calculator. Multiply π by double the radius. When using a calculator, the numbers are entered in the order of the formula. Image caption, The formula using the diameter is 𝒊 = π𝒅. Multiply π by the diameter of the circle. The formula using the radius is 𝒊 = 2π𝒓. This means that 2 is multiplied by π and then multiplied by the radius. This may be worked out without a calculator. Multiply π by double the radius. When using a calculator, the numbers are entered in the order of the formula. |
Calculating Circumference of a Circle
Solving for Diameter
- To calculate the circumference of a circle using the diameter, we use the formula C = πd. Substituting the diameter value of 9 into the formula, we get 3.142 × 9.
- The result of 3.142 × 9 equals 28.278, which rounds off to 28.28 when considering 2 decimal places. Therefore, the circumference of the circle is 28.28 m.
Solving for Radius
- When determining the circumference with the radius, we employ the formula C = 2πr. By plugging in the radius value of 3.25, the calculation becomes 2 × 3.142 × 3.25.
- The outcome of 2 × 3.142 × 3.25 results in 20.423, which, when considering 3 significant figures, simplifies to 20.4. Hence, the circumference of the circle is 20.4 cm.
Circle Circumference Examples
Understanding how to find the circumference of a circle is vital in geometry. Let's explore some examples to grasp this concept better.
Example 1: Calculating Circumference
- When given a circle with a diameter of 14 mm, we can find its circumference by using the formula C = πd. Substituting the diameter value, we get C = 14π. Therefore, the circumference is 14π mm.
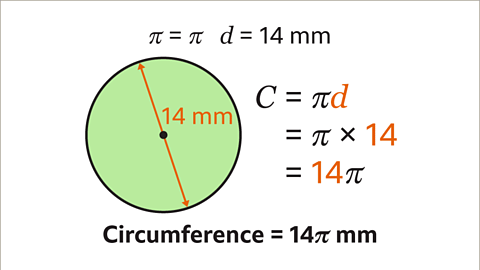
Example 2: Using Significant Figures
- For a circle with a diameter of 14 mm, the circumference can be calculated using C = πd. By substituting the diameter, we get C = 14π. This gives us the circumference as 14π mm.
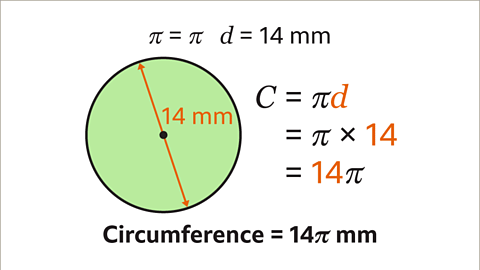
Understanding Circle Formulas
- It's important to know the formulas for finding the circumference of a circle, either using the diameter or the radius.
- For example, the formula for circumference using diameter is C = πd, where you substitute the diameter value and multiply to find the circumference.
Visual Representation
Visual aids can help us understand geometric concepts better. Below are images illustrating circle circumference calculations.
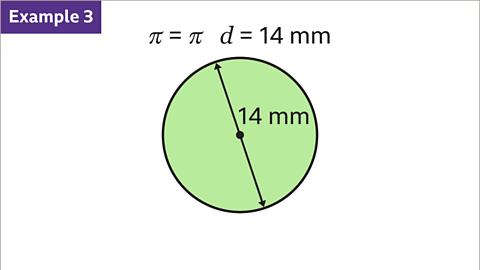 | 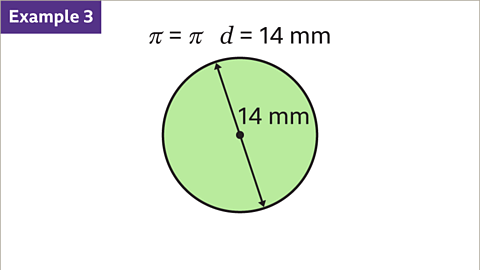 |
Calculate the diameter or radius of a circle, given its circumference
To determine the diameter and radius of a circle based on its circumference:
- Divide the circumference by π. This provides the diameter.
- The radius is half of the diameter.
Examples
Let's understand this concept with a few examples:
- When the circumference of a circle is given by the formula C = πd, it means the diameter has been multiplied by π to yield the circumference. The reverse operation is division by π to find the diameter.
- For instance, if a circle has a circumference of 465 cm, dividing this by π (taken as 3.142) gives a diameter of 148 cm when rounded to the nearest centimeter.
Example Visualization
 | 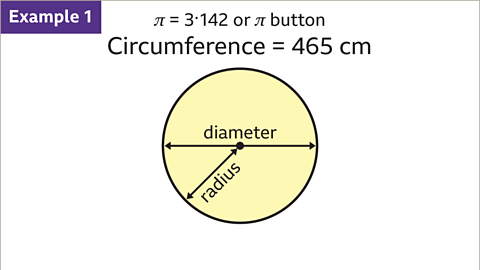 |
Further Explanation
- It's crucial to remember that the relationship between circumference, diameter, and π is fundamental in geometry.
- By dividing the circumference by π, you can find the diameter, which is essentially the distance across the circle passing through the center.
- The radius, being half of the diameter, represents the distance from the center to the edge of the circle.
- Practical applications of this concept can be found in various fields, including engineering, architecture, and physics.
Conclusion
Understanding how to calculate the diameter and radius of a circle based on its circumference is vital for various mathematical and real-world applications.
The Circle and Its Properties
Understanding Radius and Diameter
The radius of a circle is half of its diameter.
For example, if the diameter is 147.994907, then the radius is 73.99745385.
Therefore, if the diameter is 148.0140971, the radius is 74.000704854.
The radius of the circle is approximately 74 cm.
Calculating Circumference, Diameter, and Radius
The circumference of a circle is 100π m.
To find the diameter and radius:
- Divide the circumference by π to get the diameter, which is 100 m.
- The radius is half of the diameter, so it is 50 m.
| Slide | Explanation |
|---|---|
| 1 of 7 | The formula: C = πd. This formula represents the relationship between circumference and diameter. |
| 1 of 7 | The circumference of a circle is given by the formula C = πd, where the diameter is multiplied by π to get the circumference. |
Practise pi and working out circumference
Practise pi and working out the circumference of circles with this quiz. You may need a pen and paper to help you with your answers.
Quiz
- Calculating pi and finding the circumference can be fun and challenging.
- Use the formula C = 2πr to calculate the circumference of a circle.
- Remember, the radius (r) of a circle is the distance from the center to any point on the circle.
Real-life maths
 Image caption
Image captionThe age of a tree can be found by counting the concentric circles in a plane that have the same center rings in the cross-section of the trunk. In practical terms, chopping down a tree is not environmentally sound, so another method has been developed using the circumference of a tree trunk.
- Counting concentric circles helps estimate a tree's age without cutting it down.
- Measuring the circumference at a height of 1.04 m and dividing by π gives the diameter of the tree.
- Multiplying the diameter by the growth factor for the tree's species provides an estimate of the tree's age.
 Image caption
Image captionGame - Divided Islands
- Divided Islands is a strategic game that challenges players to manage resources wisely.
- Players must make decisions on how to divide limited resources among different islands.
- The game encourages critical thinking and problem-solving skills.
- Strategize to ensure the prosperity of all islands within the constraints of available resources.
















