Surface area and volume of a cylinder - Year 7 PDF Download
Key points
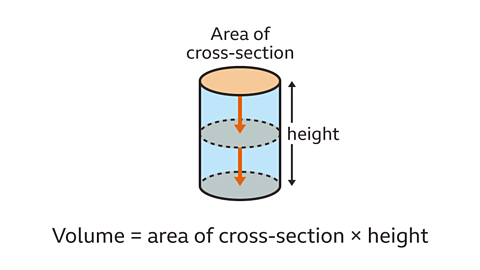 Image caption,
Image caption, A good understanding of calculations for the circumference of a circle and the area of a circle is useful when calculating the surface area and volume of a cylinder - a 3D shape with a constant circular cross-section across its length.
Cylinder in Geometry
Calculating Volume of a Cylinder
Surface Area of a Cylinder
Real-life Applications
- Cylinder Overview:
- A cylinder is a three-dimensional shape characterized by length, width, and height.
- It features a circular cross-section, which is the resulting face when a solid shape is sliced through.
- Surface Area of a Cylinder:
- The total surface area of a cylinder comprises two circular faces and a curved surface that forms a rectangle when flattened out.
- Surface area is the cumulative area of all the faces of the three-dimensional shape and is measured in square units like cm² and m².
- Volume of a Cylinder:
- The volume of a cylinder represents the space occupied by the three-dimensional shape and is measured in cubic units such as cm³ or m³.
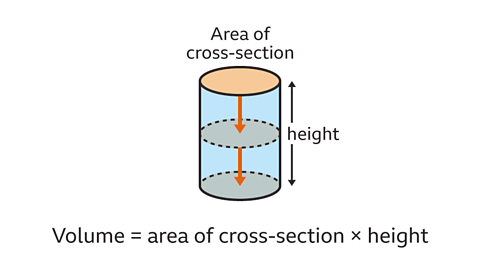
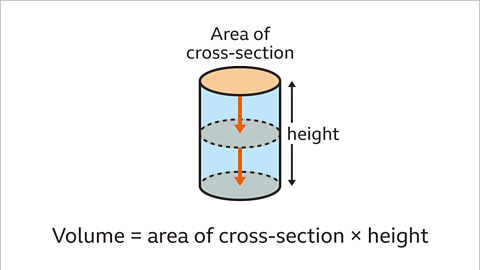
- It can be calculated by multiplying the area of its circular cross-section (a circle) by its height.
Surface Area and Volume of 3D Shapes
- Surface Area (of a 3D Shape): The total area encompassing all the faces of a three-dimensional shape. It is measured in square units like cm² and m².
- Face: Each flat surface of a solid shape.
- Volume of a Cylinder: The amount of space occupied by a cylinder, calculated by multiplying the area of its circular cross-section by its height. Volume is measured in cubic units such as cm³ or m³.
Surface Area of 3D Shapes
The surface area of a three-dimensional shape represents the sum of the areas of all its faces. For instance, if we consider a cube, which has 6 identical square faces, the surface area would be the total of these 6 squares' areas. Let's take an example:
| Shape | Number of Faces | Surface Area Formula |
|---|---|---|
| Cube | 6 | 6 x (side length)^2 |
Volume Calculation for Cylinders
The volume of a cylinder is determined by the formula: Area of the base (a circle) multiplied by the height of the cylinder. Let's understand this with an example:
Consider a cylinder with a radius of 3 cm and a height of 5 cm. The volume would be:
Volume = π x (radius)^2 x height
Volume = π x 3^2 x 5 = 45π cm³
Volume
- Volume is the amount of space that a 3D shape occupies, measured in cubic units like cm³, mm³, and m³. It can also be referred to as capacity.
Area
- Area is a measurement of the size of any plane surface or 2D shape. It is measured in square units such as cm² or m².
Visual Representation
 |
Calculate the area of a cylinder
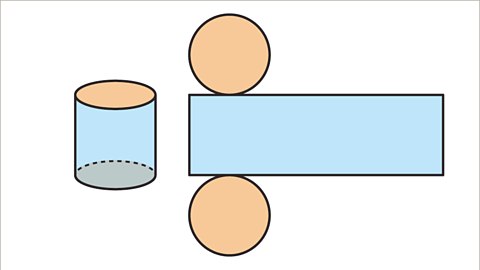
- A cylinder consists of two identical circles opposite each other and a rectangle.
- The area of a cylinder can be calculated both numerically using an approximate value for pi (π) and symbolically in terms of π.
- π (pi) is the ratio of a circle's circumference to its diameter, typically approximated as 3.14 or 3.142.
- To convert a value in terms of π to a decimal value on a scientific calculator, use the S ⟷ D button.
Understanding Pi (π)
- Pi (π) is a mathematical constant used to represent the ratio of a circle's circumference to its diameter, denoted by the Greek symbol π.
Calculations Involving Pi:
- When using a scientific calculator, the "S ➔ D" button helps convert a value in terms of π to a decimal value.
Calculating Surface Area of a Cylinder:
- To find the surface area of a cylinder:
- Calculate the area of the two circular faces (2 × π × r²).
- Determine the curved surface area, which is the rectangular face (2πr × h).
- Add the areas of the circles and the rectangle together.
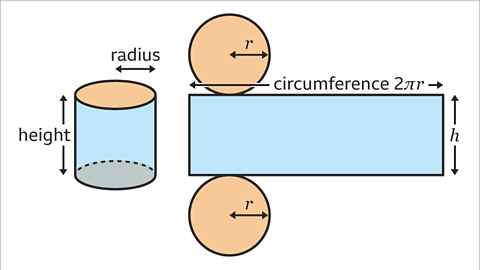
- The formula for calculating the total surface area of a cylinder is 2πr² + 2πrh, where r is the radius of the circular cross-section and h is the height of the cylinder. If the diameter (d) is given, halve it to find the radius.
- The length of the cylinder represents its height, depending on its orientation.
Understanding a Cylinder
Here is a detailed explanation about the structure and surface area of a cylinder.
Image gallery
Image gallerySkip image gallery- Structure of a Cylinder: A cylinder comprises two congruent circles and a rectangle. The circles represent the top and base faces of the cylinder, positioned opposite each other. The rectangle forms the curved surface around the cylinder.
- Calculating Surface Area: To determine the surface area of a cylinder, you use the radius and height. Each circle has a radius denoted by 'r'. The length of the rectangle is the circumference of the circular cross-section, which is 2πr. The width of the rectangle corresponds to the height of the cylinder, represented by 'h'.
- Formula for Surface Area: The total surface area of a cylinder involves the sum of two circle areas, 2πr², and the curved surface area of the rectangle, 2πrh. This gives the formula: surface area = 2πr² + 2πrh.

Cylinder Surface Area Concepts
Calculating the Surface Area of a Cylinder
- When determining the surface area of a cylinder, you need to work out the area of the circular faces and the curved surface.
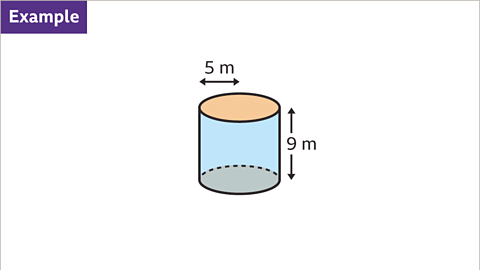
Area of Circular Faces
- The radius of the circular cross-section is crucial for finding the area of the circular faces.
- Using the formula, the area of one circular face is πr².
- With a radius of 5 m, the area of both circular faces can be calculated as 2 × π × 5² = 50π m².
- Approximating π as 3.142, the area of both circular faces is 2 × 3.142 × 5² = 157.01 m².
Curved Surface Area
- The curved surface (which appears as a rectangle when unwrapped) also contributes to the cylinder's surface area.
- Its formula is 2πrh, where r is the radius and h is the height of the cylinder.
- For a cylinder with a radius of 5 m and a height of 9 m, the curved surface area is calculated as 2 × π × 5 × 9 = 90π m².
- When approximating π as 3.142, the area becomes 2 × 3.142 × 5 × 9 = 282.078 m².
| Image 1 | Image 2 | Image 3 |
|---|---|---|
 | 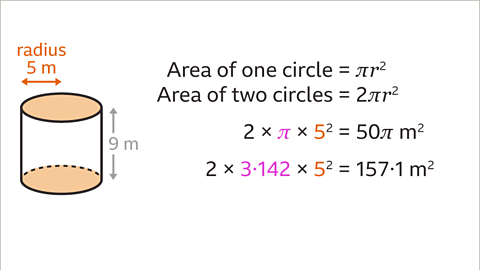 |  |
Understanding the Total Surface Area of a Cylinder
When calculating the total surface area of a cylinder, it is essential to consider the areas of the circles that form the top and bottom faces, along with the curved surface that wraps around the cylinder. Let's break down this concept further:
Theoretical Explanation:
- Sum of Areas:
- By adding the areas of the circles and the rectangle, we get 50π + 90π = 140π. This total surface area is represented as 140π m².
- Alternatively, if we approximate π as 3.142, the total area becomes 157.1 + 282.78 = 439.88 m².
- Converting to Decimal:
- The value 140π can also be expressed as a decimal by using the S↔D button on a calculator. This conversion yields 440 m² (rounded to 3 significant figures).
- Exact Calculation:
- Considering a cylinder with a total surface area of 440 m² to 3 significant figures.
Visual Representation:
- Example Scenario:
- An upright cylinder is depicted, with a height of 9 meters and a radius of 5 meters. The total surface area is labeled as 440 square meters to three significant figures.
| Slide 1 of 9 | A series of two images. The first image showcases an upright cylinder, while the second image displays the net of the same cylinder. The net includes a rectangle representing the curved surface, along with two circles attached above and below the rectangle, symbolizing the top and bottom faces of the cylinder. The circles and faces are color-coded for easy identification. |
|---|
Calculate the volume of a cylinder
- The volume of a cylinder is determined by multiplying the area of its circular cross-section by its height. This calculation is expressed by the formula \(V = \pi r^2 h\), where \(r\) represents the radius of the circular cross-section and \(h\) indicates the height of the cylinder.
Steps to find the volume of a cylinder:
- Calculate the area of the cross-section using the formula for the area of a circle: \(A = \pi r^2\).
- Multiply this area by the height of the cylinder.
Examples
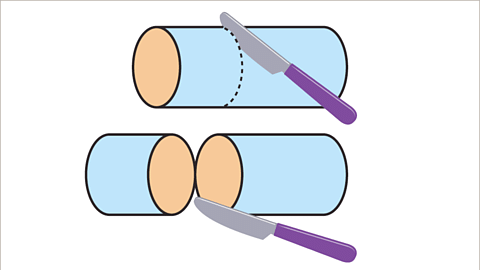
Imagine a solid cylinder being cut open, revealing a face known as the cross-section. The cross-section, always a circle, remains consistent throughout the cylinder.
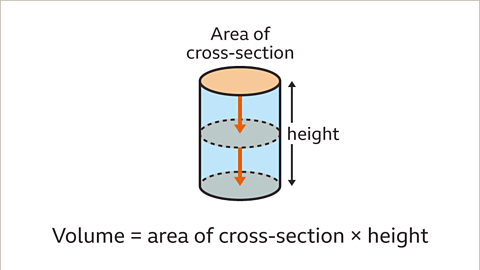
The Volume of a Cylinder
The volume of a cylinder is a fundamental concept in geometry. It is calculated by multiplying the area of the circular cross-section by the height (or length) of the cylinder. Here's how you can visualize and understand it:
- When looking at a cylinder, imagine that you are slicing it horizontally. The resulting shape is a circle, and the area of this circle is crucial in determining the cylinder's volume.
- The formula for calculating the volume of a cylinder involves the mathematical constant π (pi) and the radius of the circle. This formula can be represented as V = πr²h, where V is the volume, r is the radius, and h is the height (or length) of the cylinder.
Calculating Cylinder Volume
Let's consider an example to better understand how to calculate the volume of a cylinder:
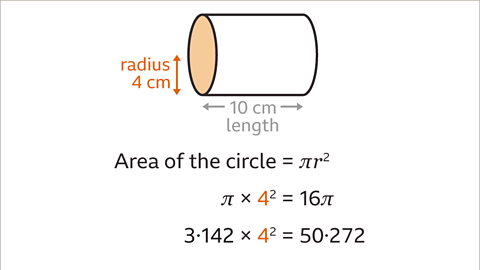
- Imagine a cylinder with a height of 10 centimeters and a diameter of 8 centimeters. To find the volume, you need to substitute these values into the formula V = πr²h.
- First, you should calculate the radius, which is half of the diameter. So, the radius (r) is 4 centimeters.
- Substitute the values into the formula: V = π x (4)² x 10. Calculate this expression to find the volume of the cylinder.
- Remember to round your answer to the nearest whole number, and you can use the approximation π ≈ 3.142 for calculations if needed.
Visualizing Cylinder Properties
Understanding the properties of cylinders can be enhanced through visual aids. Let's explore this concept further:
- Visualize how the radius, height, and diameter of a cylinder relate to each other by examining different orientations of the same cylinder.
- By observing the cylinder from various angles, you can see how the dimensions interact to determine its volume.
| Image 1 | Image 2 |
|---|---|
 |  |
The Volume of a Cylinder
Understanding how to calculate the volume of a cylinder is essential in geometry. Let's break down the process into simple steps:
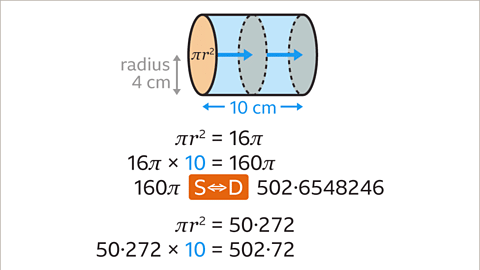
- Calculating the Cross-Section Area To start, determine the area of the circular cross-section of the cylinder, which is essentially the area of a circle. You can achieve this by using the formula for the area of a circle, A = πr². For example, if the radius is 4 units, the area would be 16π units. By approximating π as 3.142, the area becomes 50.272 units.
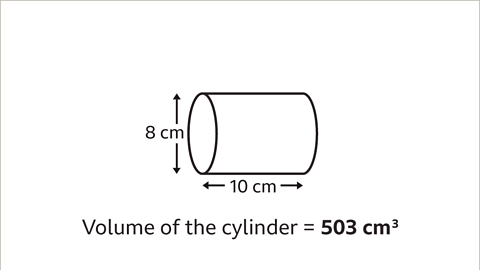
- Calculating the Total Volume Next, multiply the area of the circle by the length of the cylinder. For instance, if the area of the circle is 16π square units and the length is 10 units, the total volume would be 160π cubic units or approximately 502.72 cubic units.
- Rounding the Volume Round the calculated volume to the nearest whole number. In the previous example, both 502.65482 and 502.72 round to 503, resulting in a final volume of 503 cubic units.
- Using the Volume Formula Employ the formula V = πr²h to find the volume of the cylinder. This formula involves multiplying the area of the circular base by the height of the cylinder. Remember to use an appropriate approximation for π in your calculations.
Visual Illustrations
Here are visual representations to aid in understanding the concepts:
 |  |
 | 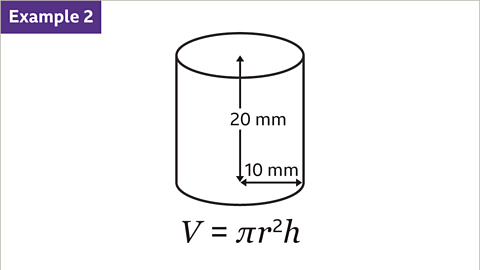 |
Volume of a Cylinder Calculation
- Substitute the value of the radius, 𝑟 = 10, and the height, ℎ = 20, into the formula V = π𝑟²ℎ, and calculate: 3.142 × 10² × 20 = 6284. The volume of the cylinder is 6284 mm³.
Visual Explanation:


Cylinder Cross-Section
- A solid cylinder sliced open reveals a cross-section, which is a circle with the same area throughout.
Visual Explanation:
Slide 1 of 10, A series of two images. The first image shows a horizontal cylinder being sliced vertically by a knife, with a dashed curve indicating the cut. The second image displays the result – the cylinder in two pieces, each with the same cross-sectional area. The circular faces are orange, and the curved surface is blue. Imagine a solid cylinder being sliced open, revealing a consistent circular cross-section.Slide 1 of 10, A series of two images. The first image shows a horizontal cylinder being sliced vertically by a knife, with a dashed curve indicating the cut. The second image displays the result – the cylinder in two pieces, each with the same cross-sectional area. The circular faces are orange, and the curved surface is blue. Imagine a solid cylinder being sliced open, revealing a consistent circular cross-section.Practise finding the surface area and volume of cylinders
Practice calculating the surface area and volume of cylinders with this interactive exercise. Grab a pen and paper to aid you in your calculations.
Real-life maths

Certain food items, like baked beans, vegetables, fish, and meat, are commonly packaged in cylinder-shaped containers. Cylindrical tins efficiently fit into boxes for transportation, utilizing about 90% of the available space.
The circular cross-section of these containers enables them to withstand pressure during storage, ensuring the food inside has a long shelf life.
Manufacturers must accurately calculate the surface area of these containers, including a small additional area for seams. The volume of the cylinder dictates the quantity of food that can be enclosed within the tin.
Game - Divided Islands



















