Rotation - Year 7 PDF Download
Key points
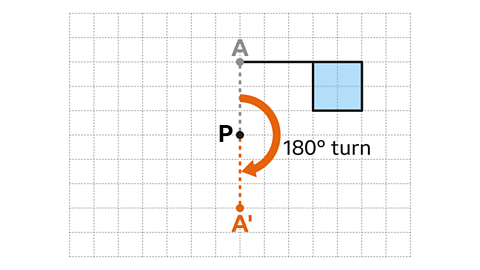 Image caption
Image caption Rotation
- A rotation is a turning effect applied to a point or shape.
- Rotations are one of the four types of transformations, alongside translations, reflections, and enlargements.
Transformation
- Transformation refers to a change in position or size of a shape.
- Transformations include translations, reflections, rotations, and enlargements.
- Rotation in Geometry
- Definition: A rotation in geometry refers to a transformation that has a turning effect on a shape. It results in a congruent shape, meaning the shape remains the same shape and size, making them identical.
- Center of Rotation: When a shape is rotated, it turns around a fixed point known as the center of rotation. This point can be located inside the shape, at a vertex of the shape, or even outside the shape.
- Example: Imagine rotating a square around a point within the square. The square will maintain its size and shape but will be positioned differently.
- Direction of Rotation
- Clockwise and Anti-clockwise Rotation: Rotations can be either clockwise (in the same direction as the hands of a clock) or anti-clockwise (in the opposite direction to the hands of a clock). Typically, rotations are done in multiples of 90 degrees (90°, 180°, or 270°).
- Example: Think of rotating a triangle 180 degrees in a clockwise direction. The resulting triangle will be in a completely inverted position compared to the original triangle.
Rotations
Rotations in Geometry involve moving a shape around a center of rotation. There are two main directions in which rotations can occur:
- Clockwise: Travelling in the same direction as the hands on a clock.
- Anti-clockwise: Travelling in the opposite direction to the hands on a clock.
Understanding Rotations
To understand rotations, a good grasp of angles and rotational symmetry is beneficial. When a shape undergoes a rotation, it pivots around a central point by a certain angle in a specific direction.
Describing a Rotation
When describing a rotation, three key elements need to be specified:
- Angle of Rotation: The amount of rotation in degrees.
- Direction: Clockwise or anti-clockwise.
- Center of Rotation: The point around which the shape is rotated.
For instance, imagine rotating a square by 90 degrees in a clockwise direction around its center. The square would appear differently but maintain its original shape.
Remember, rotations play a crucial role in various fields such as art, design, and engineering, allowing us to manipulate and transform shapes and objects.
| Angle of Rotation | Direction | Center of Rotation |
|---|---|---|
| 90 degrees | Clockwise | Center of the shape |
| 180 degrees | Anti-clockwise | Vertex of the shape |
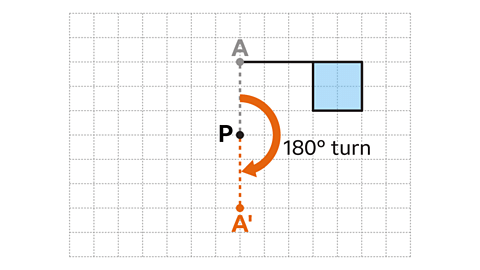 Image captionBack to top
Image captionBack to topRotating about the centre of a shape
When a shape is rotated about a central point, the starting shape and the resulting image will always overlap.
- Rotation: It is a turning effect applied to a point or shape. This transformation involves changing the orientation of the object about a fixed center.
- Object: Refers to the initial shape before any transformation takes place. It serves as the baseline for the rotation.
- Image: Represents the final position of the shape after the rotational transformation has been applied. It is where the object ends up after rotation.
When a shape is rotated, using a piece of tracing paper can be a helpful tool for plotting and visualizing the rotation.
How to Determine the Position of a Rotated Shape
- Place a sheet of tracing paper over the original shape.
- Trace the shape onto the tracing paper.
- Rotate the tracing paper in the specified direction and angle while keeping the center of rotation fixed.
- The rotated shape will now be visible on the tracing paper.
- Remove the tracing paper and draw the shape in its new position.
Examples
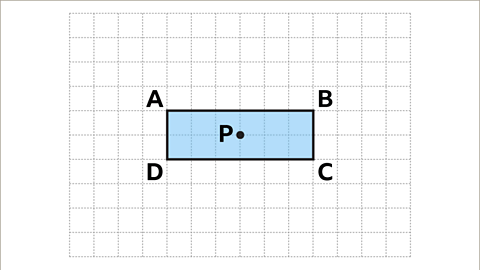
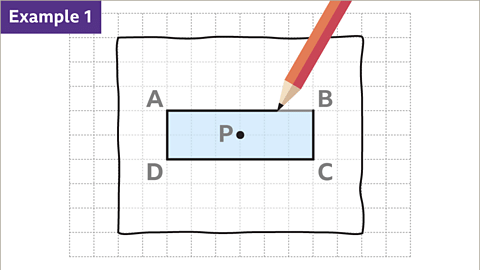
- Image caption: Rectangle ABCD is to be rotated 90 degrees clockwise around the center of rotation, P.
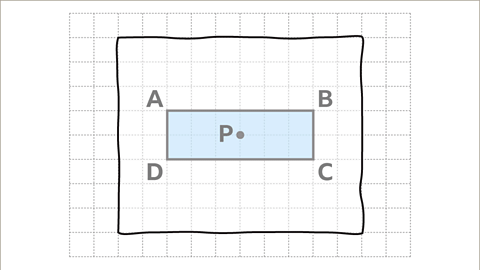
- Image caption: Place the tracing paper over the shape and center of rotation.
- Image caption: Trace the shape with a pencil and mark the center of rotation.
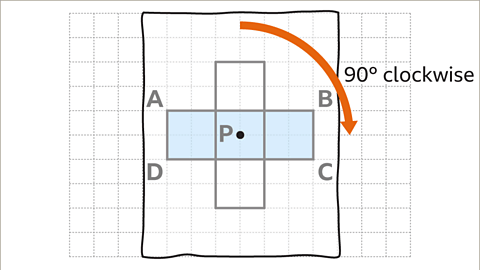
- Image caption: Turn the tracing paper 90 degrees clockwise while keeping the center of rotation fixed at point P.
Geometric Rotations Study Guide
Rotation of Shapes
Rotation of Rectangle
When a rectangle A'B'C'D' is rotated 90° clockwise about point P:
Draw the shape in its new location and label the vertices accordingly.

Rotation of Trapezium on Axes
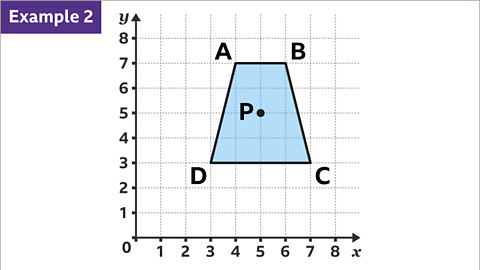
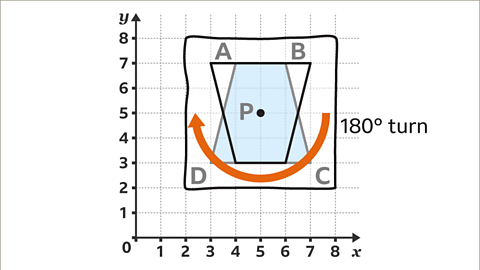
For instance, when Trapezium ABCD is rotated 180° about point P with coordinates (5, 4):
Plot the shape on a set of axes, mark the center of rotation, and perform the rotation.
Tracing Paper Technique
To rotate a shape using tracing paper:
Overlay the shape with tracing paper, trace it, mark the center of rotation, and perform the rotation.
Rotating Traced Shape
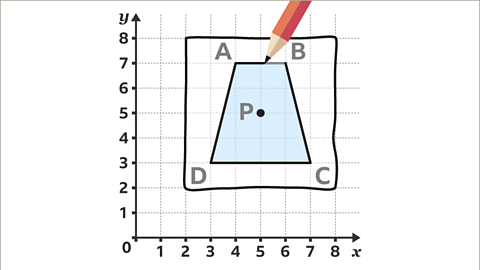
To rotate the traced shape 180°:
Turn the tracing paper while keeping the center of rotation fixed at point P.
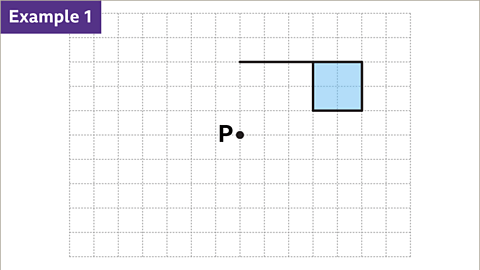
Rotations and Shapes
- Image caption, Draw the shape in its new location. The new shape can be labelled with similar letters to explain where each vertex has been rotated to. Trapezium A'B'C'D' is a 180° rotation about point, P.
- Image caption, To fully describe a rotation, it is necessary to specify the angle of rotation, the direction, and the point it has been rotated about. Triangle A'B'C' is a rotation 90° anti-clockwise (or 270° clockwise) about point P.
Example of Rotations
- Image caption, An image of a square grid. The grid has a length of fourteen squares and a width of ten squares. A rectangle of length six squares and width two squares has been drawn on the grid. Each vertex, starting with the top left, is labelled A, B, C, and D in a clockwise direction. The centre point of the rectangle has been marked and labelled, point P. Rectangle ABCD is to be rotated 90° clockwise about the centre of rotation, P.
Illustrative Examples
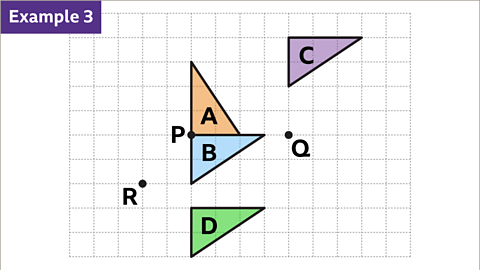
- Example three. An image of a square grid. The grid has a length of fourteen squares and a width of ten squares. An isosceles triangle has been drawn on the grid. Triangle A B C, starting from the top vertex, A, has a diagonal side of length two squares to the left and six squares down, a side of length four squares to the right, with the final diagonal side joining back to the starting point. Each vertex is labelled A, B, and C in an anti clockwise direction. A point, four squares below vertex A has been marked and labelled, point P. A second triangle has been drawn to represent a rotation. The rotation is ninety degrees anti clockwise, about point P. In the new shape, vertex A, dash, is two squares to the left and two squares above vertex B. Vertex, B, dash, is in the same place as vertex C. Vertex, C, dash, is two squares to the right and two squares below vertex A. Drawn left: A curved, anti clockwise arrow, one quarter of a full turn. Written left: ninety degrees anti clockwise.
1 of 10
Slide 1 of 10, An image of a square grid. The grid has a length of fourteen squares and a width of ten squares. A rectangle of length six squares and width two squares has been drawn on the grid. Each vertex, starting with the top left, is labelled A, B, C, and D in a clockwise direction. The centre point of the rectangle has been marked and labelled, point P. Rectangle ABCD is to be rotated 90° clockwise about the centre of rotation, P.Question
Back to topRotating about other centre of rotations
- Effect of Centre of Rotation:
- The position of the centre of rotation impacts the final image location.
- When the rotation center coincides with a vertex of the object, that vertex remains unchanged through the rotation.
- Definition of Vertex:
- A vertex is a point where two or more lines intersect, commonly found at the corners of shapes.
- Vertices do not alter during a transformation process.
- Plotting Rotations:
- It is feasible to visualize a rotation without the need for tracing paper.
How to Determine the Position of a Shape after Rotation
- Visualize a line extending from the center of rotation to a vertex on the shape.
- Rotate this line in the correct direction by the specified angle while keeping the center of rotation fixed.
- The endpoint of this line will correspond to the new location of that vertex on the shape.
- Repeat this process for each vertex on the shape.
Examples
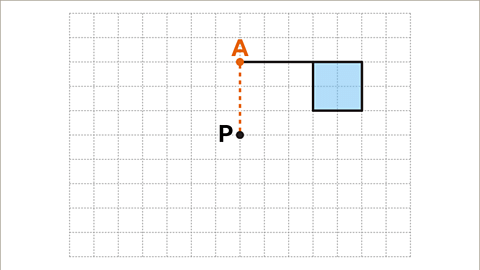
- Rotate the flag shape 180 degrees around the center of rotation, point P.
- Choose a vertex on the shape, such as A, and imagine a line from the center of rotation, P, to that vertex.
 |  |
Understanding Rotations in Geometry
Rotating shapes is a fundamental concept in geometry. When a shape is rotated, it is turned around a point known as the center of rotation. Let's delve into the details of rotational transformations:
Rotation of Line Segments
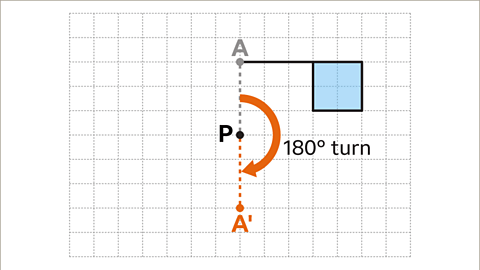
- Rotating a Line Segment 180°: When a line segment is rotated 180° around a fixed point, the direction of rotation (clockwise or anticlockwise) doesn't affect the outcome. The new position of the endpoint is reflected as A'.
- Rotating Another Line Segment: By choosing a different vertex B and rotating the line from P to B by 180°, the new position of point B can be determined.
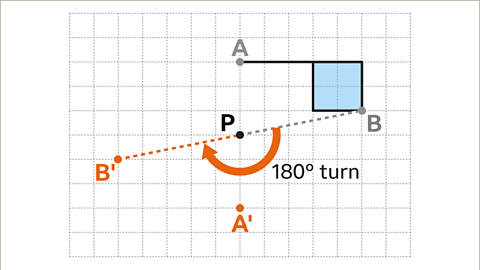
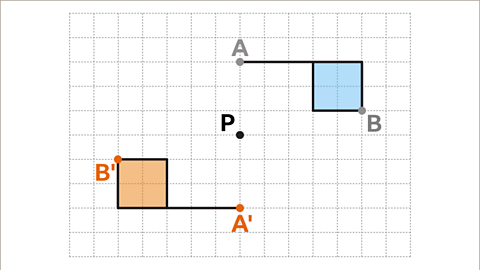
Completing the Image
- Finishing the Rotation: By repeating the rotation process for all necessary vertices, the entire image can be drawn accurately. Verification can be done using tracing paper if needed.
Rotating Triangles
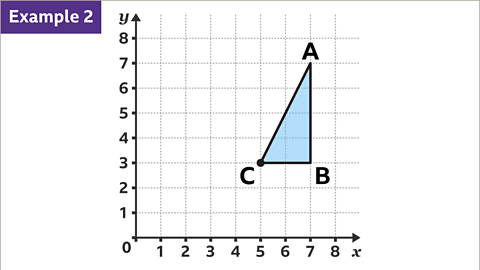
- Rotating Triangle ABC: When rotating triangle ABC 90° anticlockwise around vertex C, the center of rotation, vertex C remains unchanged.
Rotational Symmetry and Transformations
Rotational symmetry is a fundamental concept in geometry that involves rotating shapes around a fixed point. Let's explore this concept further:
Rotating Line Segments
- When a line segment AC is rotated 90 degrees anticlockwise around point C, the new position of point A becomes (1, 5).
- Similarly, rotating line segment BC by 90 degrees anticlockwise around point C results in point B moving to (5, 5).
Completing Rotated Shapes
- By plotting all three vertices of a shape after a 90-degree anticlockwise rotation around vertex C, we can complete the rotated shape.
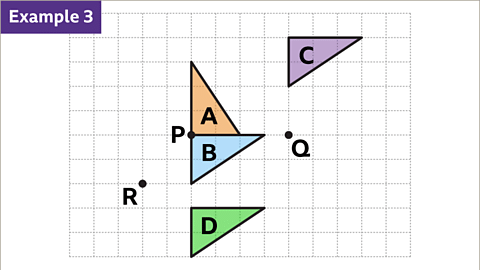
Effects of Center of Rotation
- The center of rotation significantly influences the final position of a shape after rotation. For instance, rotating triangles A, B, C, and D by 90 degrees clockwise about different points results in similar orientations but different positions on the grid.
Visual Example
 |  |
Overview
- Illustration of a square grid with dimensions and a flag shape drawn on it.
- Rotation of the flag shape by 180 degrees around point P.
Details
Image Description
- A square grid is depicted, measuring fourteen squares in length and ten squares in width.
- A flag shape is illustrated on the grid, comprising a horizontal line of five squares.
- At the right end of the line, a square is drawn by extending two squares down, two squares to the left, and two squares up.
- A point labeled as P is marked three squares below the left end of the line.
Transformation
- The flag shape is rotated 180 degrees around the center of rotation, point P.
Question
- Paraphrase the given information and provide detailed explanations with relevant examples.
- Present all points in a bullet format with appropriate headings.
- Ensure that no topic is overlooked.
Practise rotation and rotating a shape about a given point
Quiz
Practise rotation and how to rotate a shape about a given point in this quiz. You may need a pen, paper and tracing paper for this quiz.
- Rotation Practice Quiz
- Try your hand at rotating shapes around specific points.
- Use pen, paper, and tracing paper to enhance your understanding.
Real-life maths

A gymnast is required to perform complicated tumbling when competing on a variety of apparatus or as a floor exercise. Many of these routines involve acrobatics where the competitor is rotating.
For example, on the pommel horse a gymnast can perform a move called circles. Circles requires the competitor to rotate or swing their legs around the apparatus whilst alternating their hand positions on the pommels (handles). Some events require an elaborate dismount. This could include a somersault where a person's body rotates 360°.

Game - Divided Islands
- Game Overview
- Explore a challenging puzzle game on Divided Islands.
- Test your strategic skills in dividing and conquering territories.














