Polygons - sum of interior angles - Year 7 PDF Download
Key points
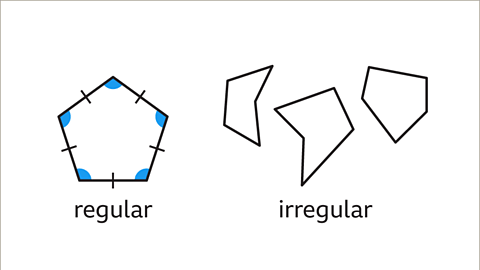 Image caption
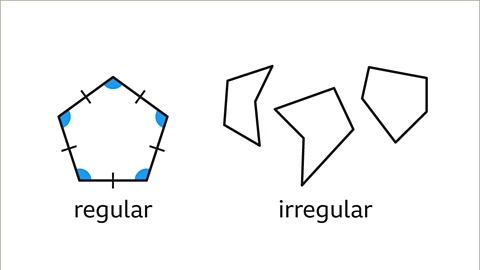
Image caption- A polygon is a closed 2D shape with at least three sides. A regular polygon is a polygon with all equal sides and angles. An irregular polygon is a polygon where this is not the case. Understanding the contrast between regular and irregular polygons is crucial for determining missing angle measurements.
- In order to calculate the size of missing interior angles in polygons, it is essential to grasp the following angle sums:
- The interior angles of a triangle add up to 180°.
- The interior angles of a quadrilateral (a 2D shape with 4 edges and 4 vertices) sum to 360°.
- The interior angles of a pentagon (a polygon with five sides) sum to 540°.
- Generally, the interior angles of any polygon sum up to (number of sides - 2) × 180°.
- To determine the size of one interior angle of a regular polygon, divide the sum of the interior angles by the number of sides.
- To find the size of a missing interior angle in an irregular polygon, subtract the sum of the given angles from the sum of the interior angles.
- A regular polygon is a shape with all sides and angles being equal. Conversely, an irregular polygon lacks this uniformity. Understanding this disparity is crucial for determining missing angles.
- For instance, a regular polygon exhibits identical sides and angles.
- In contrast, an irregular polygon demonstrates varying side lengths and angles.
- This distinction aids in calculating missing angles effectively.
- Calculating Interior Angles in Polygons
- To ascertain missing interior angles in polygons, understanding the total sum of interior angles is essential:
- The interior angles of a triangle total 180 degrees.
- A quadrilateral, a four-sided polygon with four vertices, has interior angles totaling 360 degrees.
- A pentagon, a polygon with five sides, possesses interior angles totaling 540 degrees.
- Generally, the sum of interior angles in any polygon equals (number of sides - 2) multiplied by 180 degrees.
- Interior Angles of Specific Polygons
- The interior angles of a triangle sum up to 180 degrees.
- A quadrilateral, characterized by four edges and vertices, has interior angles summing up to 360 degrees.
- The interior angles of a pentagon, a five-sided polygon, total 540 degrees.
- General Rule for Interior Angles
- For any polygon, the sum of interior angles can be calculated using the formula: (number of sides - 2) multiplied by 180 degrees.
- Calculating Interior Angles of Regular Polygons
- To determine the measure of one interior angle of a regular polygon, divide the total sum of interior angles by the number of sides.
- To determine the size of a missing interior angle in an irregular polygon, you can calculate it by subtracting the sum of the given angles from the total sum of interior angles.
Video
You can refer to the video tutorial to understand how to compute the total interior angles of any polygon effectively.
Finding the Total Interior Angles in Polygons
- Interior angles refer to the angles located inside a shape.
- In any triangle, the sum of interior angles always adds up to 180 degrees.
- Any polygon, which is a two-dimensional shape with three or more edges and vertices, can be divided into smaller triangles (fewer in number than the polygon's sides).
- The total of the interior angles in any polygon can be determined using the following formula:
Breaking Down the Concept of Interior Angles
Interior angles are the angles enclosed within a shape. They are integral in understanding the overall geometry of the figure.
For instance, in a triangle, where there are three sides, the sum of the interior angles always amounts to 180 degrees. This fundamental rule holds true for all triangles.
Application of Interior Angles in Polygons
When dealing with polygons, the understanding of interior angles is crucial. By dividing a polygon into triangles, you can easily calculate the total sum of its interior angles.
Consider a square, which is a four-sided polygon. By converting it into two triangles, you can ascertain the total interior angles by summing up the angles in each triangle.
Understanding Polygons and Interior Angles
- Any polygon, a 2D shape with three or more edges and vertices, can be split into two triangles, which is fewer than the number of sides of the polygon.
Calculating Interior Angles of Polygons
- The sum of the interior angles of a polygon can be determined using a formula:
- Sum of interior angles = (number of sides - 2) × 180°
| Polygon | Number of sides | Formula | Sum of interior angles |
|---|---|---|---|
| Triangle | 3 | (3 - 2) × 180 | 180° |
| Quadrilateral | 4 | (4 - 2) × 180 | 360° |
| Pentagon | 5 | (5 - 2) × 180 | 540° |
| Hexagon | 6 | (6 - 2) × 180 | 720° |
| -sided polygon | (-2) × 180 | (-2) × 180° |
Examples
- When looking at a quadrilateral, the reason the interior angles sum up to 360° is because a quadrilateral can be divided into two triangles. Each triangle's angles sum up to 180°, so together, the two triangles sum to 360°.

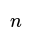
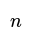
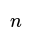
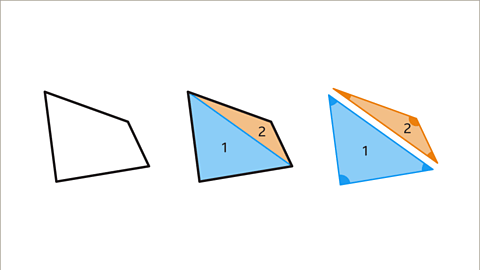
Understanding Polygon Interior Angles
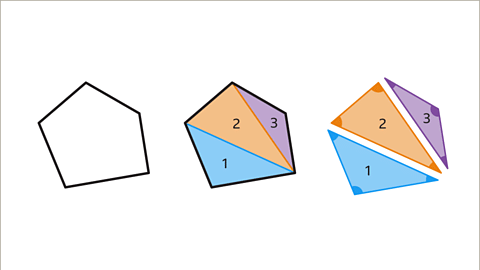
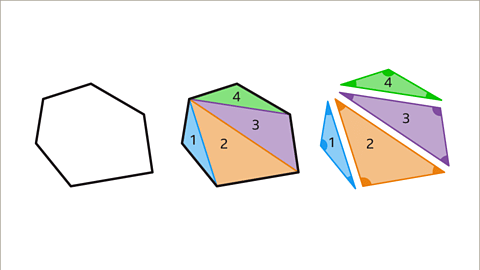
Interior angles of polygons can be understood by dividing them into triangles:
- Triangles in a Pentagon: When a pentagon is divided into three triangles, each interior angle sums up to 180 degrees. Therefore, the total sum of interior angles in a pentagon is 540 degrees.
- Triangles in a Hexagon: By dividing a hexagon into four triangles, the sum of its interior angles amounts to 720 degrees, as each triangle contributes 180 degrees.
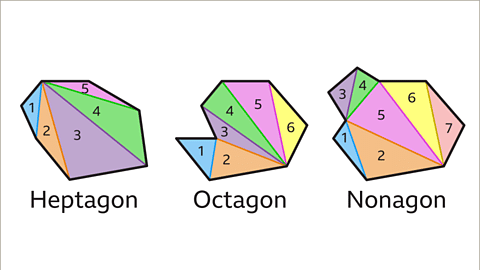
- Pattern in Polygon Division: The number of triangles a polygon can be split into is always two less than the number of its sides. This pattern is represented as (𝑛 – 2), where 𝑛 signifies the number of sides.
- Examples of Polygon Division: Various polygons like heptagons, octagons, and nonagons can be divided into corresponding numbers of triangles, each showcasing a distinct color scheme.
- Decagon Interior Angles: Exploring an irregular decagon, its interior angles' total can be determined using different methods, providing a deeper understanding of polygon properties.
Visual Representation
 |  |
 | 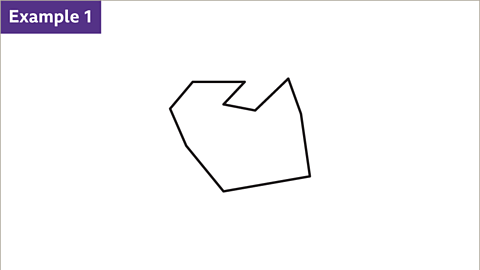 |
Decagon (10-sided polygon)
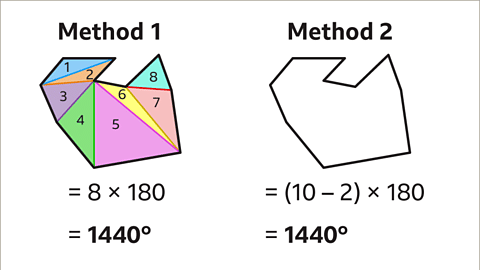
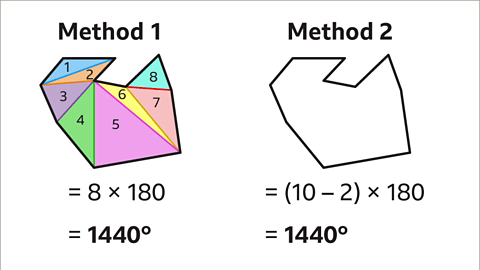
- Image caption: To find the sum of interior angles in a decagon, we can employ different methods.
- Method 1: Divide the decagon into triangles and multiply by 180°. This results in 1440°.
- Method 2: Utilize the formula: sum of interior angles = (sides - 2) × 180. For a decagon, this equals 1440°.
Example Images for Decagon:
 |  |
Other Polygons
- Image caption: Exploring the interior angles of polygons beyond a decagon.
- 26-sided Polygon: The sum of interior angles in a 26-sided polygon totals 4320°.
- 53-sided Polygon: The total interior angles in a 53-sided polygon amount to 9180°.
Example Images for Other Polygons:
 |  |
Understanding Polygon Interior Angles
Case 1: Sum of Interior Angles is 1620°
When the sum of interior angles in a polygon is 1620°, we can determine the number of sides using a simple equation:
(n – 2) × 180 = 1620
By solving this equation, we find that the polygon has 11 sides.
Case 2: Sum of Interior Angles is 2160°
For a polygon with a sum of interior angles of 2160°, the process is similar:
(n – 20) × 180 = 2160
Through calculation, we determine that the polygon in this case has 14 sides.
Understanding the Concepts
Explanation of Polygon Interior Angles:
A polygon's interior angles can be found by subtracting 2 from the number of sides and multiplying by 180.
Example:
Consider a polygon with 7 sides. The sum of its interior angles would be (7 - 2) × 180 = 900°.
Visual Representation


Key Concept: Quadrilaterals and Triangle Division
Explanation:
A quadrilateral can be divided into two triangles. The sum of interior angles in a triangle is 180°, so the total interior angles in a quadrilateral sum to 360°.
Example:
Dividing a quadrilateral into triangles helps in understanding why the interior angles sum up to 360°.
Visual Aid


| Slide 1 of 10 | A series of three images showing the concept of dividing a quadrilateral into triangles to understand interior angles. |
|---|
Question
Back to topFinding missing interior angles in polygons
- A regular polygon is a shape where all sides and angles are equal. In such polygons, hash marks are used to indicate equal side lengths, making it easy to identify which sides are the same length. When the sum of interior angles is known, dividing this total by the number of sides reveals the measure of each angle.
- An irregular polygon, in contrast, has sides and angles that are not equal. Determining the measure of a single angle in an irregular polygon is challenging unless all other angles are provided.
Understanding Polygon Properties
Hash Marks
Short lines marked on the side or edge of a shape. The same number of marks indicate equal lengths. When hash marks are present on each side, it means those sides are equal. A polygon is considered regular if all sides are marked with a single hash mark.For example, consider a square. Each side is marked with a hash, indicating that all sides are of equal length.
Interior Angles
The angles inside a shape. If the sum of the interior angles is known, dividing by the number of sides will give the size of one angle.For instance, in a triangle, the sum of interior angles is always 180 degrees. So, for a triangle with 3 sides, each angle measures 60 degrees (180 divided by 3).
Irregular Polygons
An irregular polygon is a polygon where all sides and angles are not equal. In an irregular polygon, it is not possible to find the size of one angle unless all other angles are known.Imagine a shape with sides of different lengths and angles of varying measures, like a kite. In such cases, determining a single angle without additional information about the other angles is challenging.
Understanding Irregular Polygons
- It is impossible to determine the size of a single angle in an irregular polygon without knowledge of all other angles.
Examples
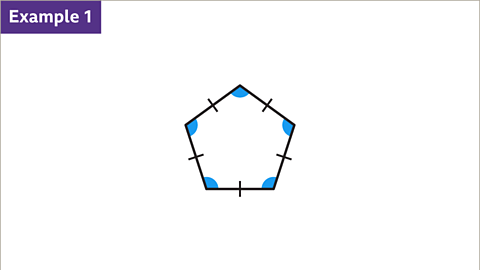
- These polygons are all pentagons. Only the one on the left is regular, as indicated by equal side lengths.
- Find the size of one interior angle of a regular pentagon by knowing the sum of interior angles, calculated as (n - 2) × 180, where n is the number of sides.
- A regular pentagon has five angles, each measuring 108°, derived by dividing the sum of interior angles (540°) by the number of angles.
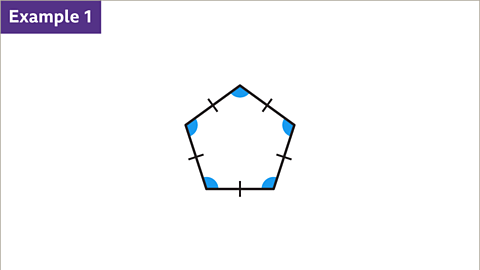
- A regular pentagon's interior angles are all equal, each measuring 108°, obtained by dividing the total sum of angles (540°) by the number of angles.
Regular Polygons
- Regular Octagon Interior Angles:
Each interior angle in a regular octagon measures 135 degrees.
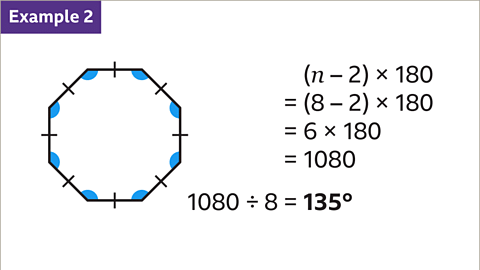
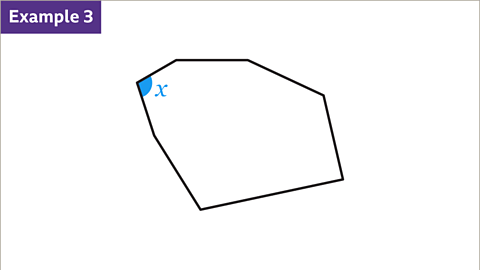
Irregular Polygons
- Irregular Heptagon - Unknown Angle:
The size of an angle in an irregular heptagon cannot be determined without additional angle measurements.
- Irregular Heptagon - Finding a Missing Angle:
To find a missing angle in an irregular heptagon, calculate the sum of known angles and subtract it from 900 degrees.
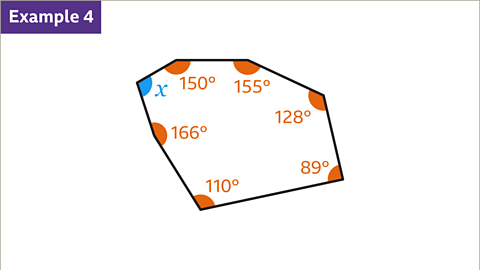
Geometry Concepts
- Find the final missing angle in an irregular nonagon:
- The sum of interior angles in a nonagon is 1260°, calculated by (9 - 2) x 180.
- To determine the final missing angle, subtract the sum of known angles (1043°) from 1260°.
- Therefore, the final angle is 217°.
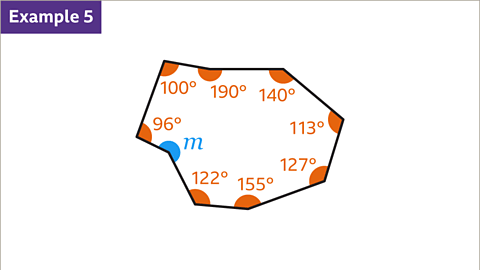
- Find the missing angle in an irregular hexagon:
- The total of interior angles in a hexagon is 720°, calculated by (6 - 2) x 180.
- By subtracting the sum of given angles (390°) from 720°, you find that 3 angles combined equal 330°.
- Therefore, each angle is 110°.
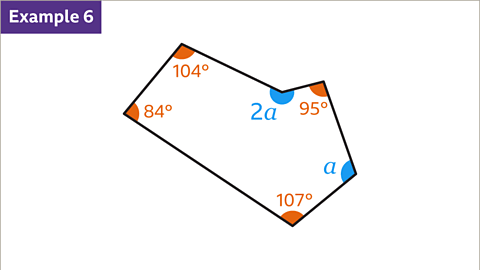
Understanding Polygon Types
These polygons are all pentagons. Only the one on the left is regular, as indicated by the equal side lengths.
Slide 1 of 8, A series of four images showing regular and irregular pentagons.Question
Back to topPractise the sum of interior angles of polygons
Practise finding the size of interior angles of polygons with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Back to topGame - Divided Islands
Back to topUnderstanding Interior Angles of Polygons
Interior angles are angles on the inside of shapes like polygons.
For example, a triangle has three interior angles, a quadrilateral has four, and so on.
Calculating Interior Angles
To find the sum of interior angles in a polygon, you can use the formula: (n-2) * 180, where n represents the number of sides.
For instance, a hexagon (6 sides) has interior angles summing up to 720 degrees.
Practicing with a Quiz
Engage in quizzes to enhance your understanding of interior angles in polygons.
Remember to use pen and paper to work out your answers effectively.
Game - Divided Islands
Explore fun games like "Divided Islands" to apply your knowledge of interior angles in a practical scenario.
Games can make learning more interactive and enjoyable.



















