Properties of Quadrilaterals - Year 7 PDF Download
Key points
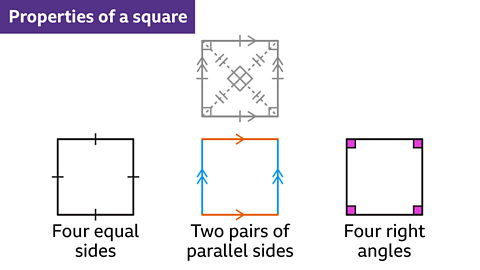 Image caption
Image captionQuadrilaterals
- Quadrilaterals are 2D shapes with 4 edges and 4 vertices.
- They are polygons, which are closed 2D shapes bounded by straight lines.
- Quadrilaterals have four equal sides and four right angles.
- They are classified based on the lengths and positions of their edges.
Understanding Quadrilaterals
- The angles in a quadrilateral always add up to 360 degrees.
- Quadrilaterals have specific properties related to their diagonals and lines of symmetry.
- A particular property may be common to more than one type of quadrilateral.
Angles in a Quadrilateral
In any quadrilateral, the total of all angles is 360 degrees. This means that when you add up all the angles inside a four-sided shape, the result will always be 360 degrees.
Properties of Quadrilaterals
Quadrilaterals exhibit distinct characteristics concerning their diagonals and lines of symmetry. Let's understand these properties:
- Diagonals: Diagonals are lines that connect non-adjacent vertices of a polygon. In quadrilaterals, diagonals connect opposite corners.
- Line of Symmetry: A line of symmetry divides a shape into two equal parts, where one side mirrors the other. It is as if you could fold the shape along this line and the two halves would match perfectly.
Common Properties across Quadrilaterals
It is important to note that certain characteristics may apply to more than one type of quadrilateral. Let's consider an example to clarify:
- Example: Both rectangles and squares have four right angles, making this a common property between these two types of quadrilaterals.
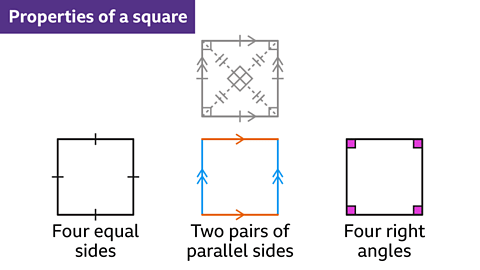 Image caption, Back to top
Image caption, Back to top Properties of squares, rhombuses, and rectangles
- Quadrilaterals
- A quadrilateral is a 2D shape with 4 edges and 4 vertices.
- A square is a regular quadrilateral with all four sides equal in length and all angles being right angles.
- A rhombus is a quadrilateral with two pairs of parallel sides and all sides being equal.
- A rectangle is a quadrilateral with opposite pairs of sides that are both equal in length and parallel, and all angles are right angles.
- Square
- A square is a geometric shape with four sides of equal length.
- It also has two pairs of parallel sides.
- Four right angles are present within a square.
- The diagonals of a square are lines joining two non-adjacent vertices, which are equal in length.
- These diagonals bisect each other, dividing the square into two equal sections.
- Moreover, the diagonals are perpendicular to each other, forming right angles.
- A square exhibits four lines of symmetry, dividing it into equal halves that are mirror images of each other.
- Rotational symmetry is another characteristic of a square, indicating that it looks the same after a rotation through an angle between 0° and 360° about a central point.
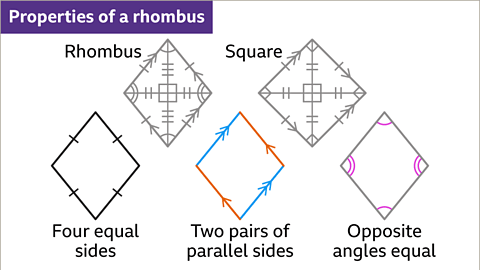
- Rhombus
- A rhombus shares similarities with a square, having four sides of equal length and two pairs of parallel sides.
- Additionally, it possesses two pairs of equal opposite angles.
- Similar to a square, the diagonals of a rhombus bisect each other and are perpendicular.
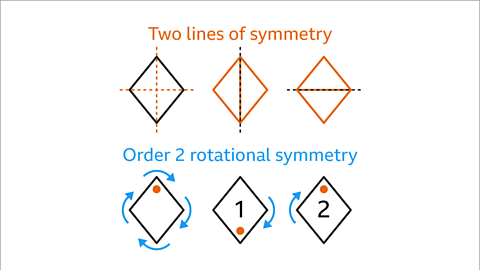
- It features two lines of symmetry and rotational symmetry of order 2.
- Rectangle
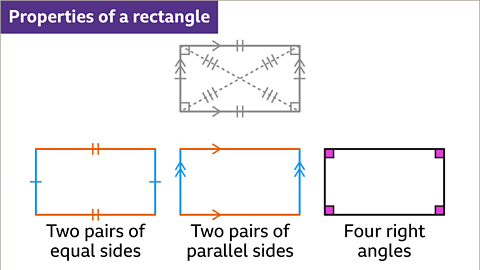
- A rectangle is characterized by having two pairs of opposite sides that are equal in length.
- It also has two pairs of parallel sides and four right angles.
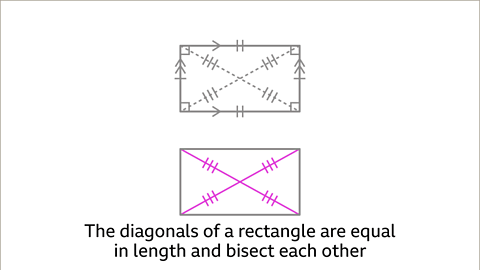
- The diagonals of a rectangle are equal in length and bisect each other.
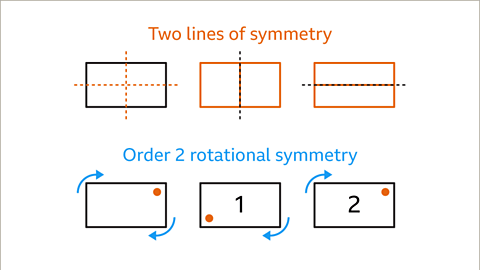
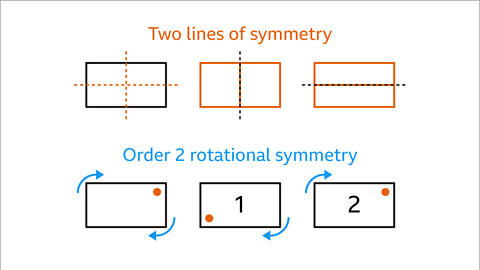
- Similar to a rhombus, a rectangle possesses two lines of symmetry and rotational symmetry of order 2.
Properties of a Quadrilateral
- Four sides are equal in length.
- Two pairs of sides are parallel.
- It has four right angles.
- Diagonals are lines joining non-adjacent vertices of a polygon and are equal in length.
- These diagonals bisect each other and are perpendicular.
- It possesses four lines of symmetry, dividing the shape into two equal parts that are mirror images of each other.
- Rotational symmetry is present, indicated by a shape looking the same after a rotation of a certain angle (greater than 0 degrees and less than 360 degrees).
Rhombus Characteristics
- A rhombus features:
- Four sides of equal length.
- Two pairs of parallel sides.
- Two pairs of equal opposite angles.
- Diagonals that bisect each other and are perpendicular.
- Two lines of symmetry.
- Rotational symmetry of order 2.
Quadrilaterals Overview
- A rhombus encompasses:
- Four sides that are equal in length.
- Two pairs of parallel sides.
- Two pairs of equal opposite angles.
- Diagonals that bisect each other and are perpendicular.
- Two lines of symmetry.
- Rotational symmetry of order 2.
- A rectangle is defined by:
- Two pairs of opposite sides that are equal in length.
- Two pairs of parallel sides.
- Four right angles.
- Diagonals that are equal in length and bisect each other.
- Two lines of symmetry.
- Rotational symmetry of order 2.
Examples
Image gallerySkip image gallery- Image caption: All quadrilaterals have four sides and four angles. The lengths and positions of the edges help to identify the quadrilateral. A quadrilateral that is not a specific type is called an irregular quadrilateral.
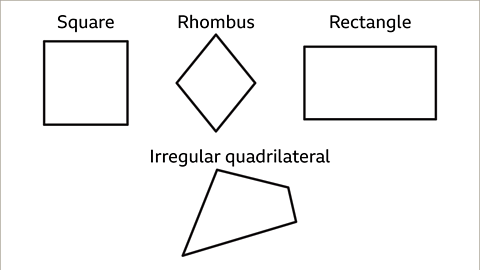 Image caption
Image captionAll quadrilaterals have four sides and four angles. The lengths and positions of the edges help to identify the quadrilateral. A quadrilateral that is not a specific type is called an irregular quadrilateral.
Square Properties
- Equal Sides and Right Angles
A square is defined by having four sides of equal length and four right angles. The sides are marked with hash marks to show their equality, while the right angles are denoted by small squares at each corner.
- Diagonals and Symmetry
The diagonals of a square are also of equal length and bisect each other at right angles. Moreover, a square exhibits four lines of symmetry. Two of these lines pass through the midpoints of opposite parallel sides, and the other two run along the diagonals.
- Rotational Symmetry
A square possesses order 4 rotational symmetry, meaning it can be rotated four times within a complete turn and still align with its original position.
Rhombus Properties
A rhombus is a special type of quadrilateral with unique characteristics and properties.
Property 1: Sides and Angles
- A rhombus has four sides of equal length.
- The opposite sides of a rhombus are parallel, forming two pairs of parallel sides.
- Opposite angles in a rhombus are equal.
- When all angles in a rhombus are right angles (90 degrees), it becomes a square.
Property 2: Diagonals
- The diagonals of a rhombus are perpendicular, intersecting at right angles.
- When the diagonals of a rhombus are equal in length, the rhombus becomes a square.
- The diagonals of a rhombus bisect each other, dividing the rhombus into equal parts.
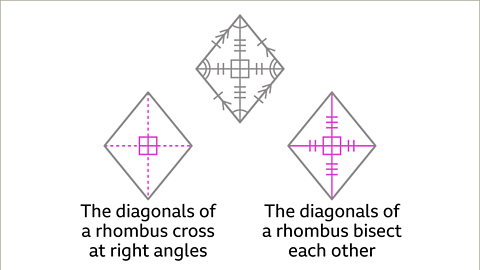
Property 3: Symmetry
- A rhombus has two lines of symmetry, which are along its diagonals.
- The lines of symmetry enable the rhombus to be cut into two mirrored halves.
- Rhombus has rotational symmetry of order 2, meaning it can fit into its outline twice in a full turn.
Rectangle Properties
Definition and Characteristics of Rectangles
A rectangle is a quadrilateral with two pairs of equal parallel sides. When all sides are equal, it becomes a square. In contrast, when the sides are unequal, it is termed an oblong. Rectangles have angles measuring 90 degrees.
Diagonals of a Rectangle
The diagonals of a rectangle are of equal length and bisect each other.
Symmetry in Rectangles
A rectangle possesses two lines of symmetry, allowing it to be divided into mirrored halves. These lines pass through the midpoints of opposite parallel sides. Additionally, a rectangle has rotational symmetry of order 2, meaning it fits into its outline twice in a complete rotation.
Quadrilaterals Overview
All quadrilaterals, including squares, rhombuses, rectangles, and irregular quadrilaterals, have four sides and four angles. The unique lengths and positions of their edges help differentiate one type from another. An irregular quadrilateral refers to a quadrilateral that doesn't fall into a specific category.
Visual Representations
 |  |  |  |
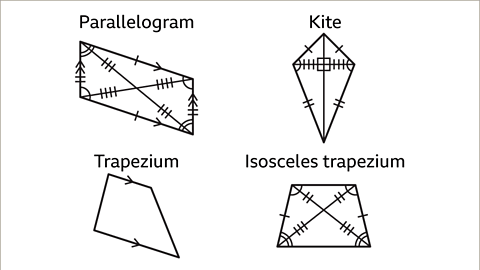
Properties of Parallelograms, Kites, and Trapeziums
- Parallelogram:
- Defined as a quadrilateral with both pairs of opposite sides being equal in length and parallel to each other.
- Opposite angles within a parallelogram are also equal.
- Example: In a parallelogram, if one pair of opposite sides measures 5 cm each and the other pair measures 8 cm each, and the opposite angles are both 90 degrees, then it qualifies as a parallelogram.
- Trapezium:
- Characterized by having exactly one pair of parallel sides.
- Example: A trapezium with one set of parallel sides measuring 6 cm each and the non-parallel sides of different lengths is a typical example of a trapezium.
- Kite:
- Consists of adjacent sides that are equal in length.
- One pair of opposite angles in a kite are also equal.
- Example: If a quadrilateral has two adjacent sides of 4 cm each and the other two sides of different lengths, with one pair of opposite angles at 60 degrees, it fits the definition of a kite.
- Parallelogram Characteristics:
- Has two pairs of opposite sides of equal length.
- Features two pairs of parallel sides.
- Contains two pairs of equal opposite angles.
- Includes diagonals, which are lines joining non-adjacent vertices and bisect each other.
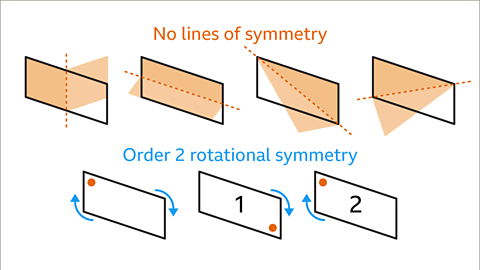
- Does not possess reflection symmetry but exhibits rotational symmetry.
- Rotational symmetry of order 2, indicating it looks the same after a rotation of 180 degrees.
- Kite Characteristics:
- Consists of two pairs of adjacent sides of equal length.
- Has one pair of opposite equal angles.
- Features diagonals of unequal lengths, one of which bisects the other.
- Possesses one line of symmetry.
- Exhibits rotational symmetry of order 1.
- Trapezium Details:
- Comprises one pair of unequal parallel sides.
- Includes diagonals of different lengths.
- Lacks reflection symmetry and rotational symmetry.
- Isosceles Trapezium Attributes:
- Consists of one pair of unequal parallel sides and two non-parallel equal sides.
- Features two pairs of adjacent equal angles.
- Contains diagonals of equal length.
- Possesses one line of symmetry.
- Does not exhibit rotational symmetry.
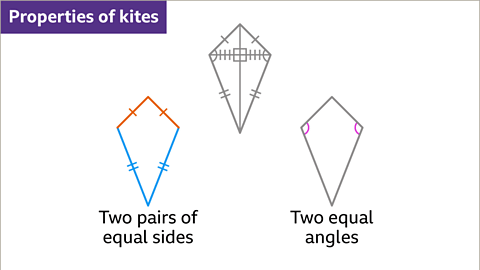
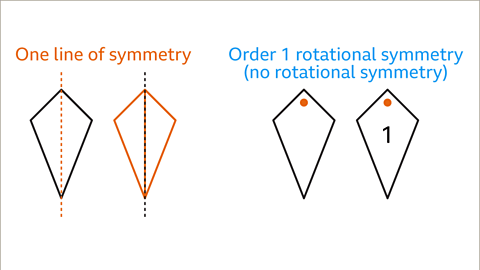
Properties of a Kite
- A kite is a quadrilateral with the following characteristics:
- Two pairs of adjacent sides that are equal in length.
- One pair of opposite equal angles.
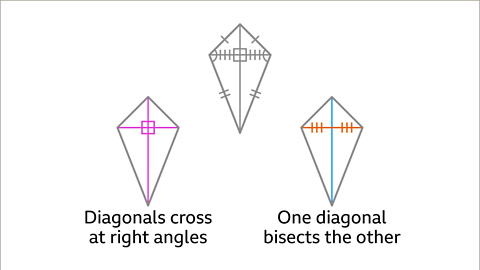
- Diagonals of unequal lengths, with one diagonal bisecting the other.
- Exhibits one line of symmetry.
- Possesses rotational symmetry of order 1.
Additional Details:
- Two pairs of adjacent sides are of equal lengths.
- Kites have one pair of opposite equal angles.
- The diagonals of a kite differ in length, with one bisecting the other.
- Kites exhibit one line of symmetry.
- Rotational symmetry of order 1 is present in kites.
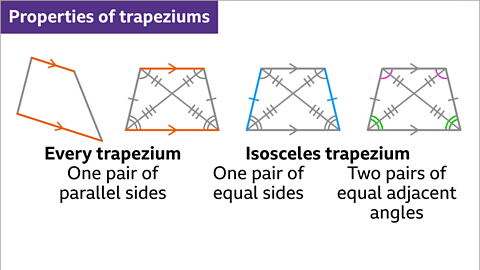
Properties of a Trapezium
- A trapezium possesses the following attributes:
- One pair of unequal parallel sides.
- Diagonals of unequal lengths.
- Lacks reflection symmetry and rotational symmetry.
Details about Trapezium:
- Trapeziums have one pair of unequal parallel sides.
- Their diagonals are of different lengths.
- They do not exhibit reflection symmetry or rotational symmetry.
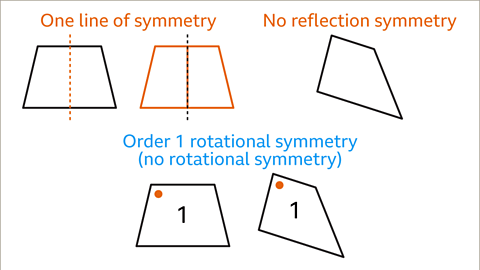
Properties of an Isosceles Trapezium
- An isosceles trapezium is characterized by:
- One pair of unequal parallel sides.
- Two non-parallel equal sides.
- Two pairs of adjacent equal angles.
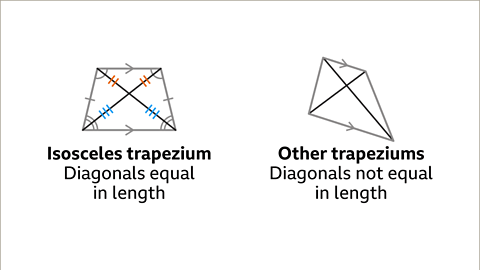
- Diagonals of equal lengths.
- One line of symmetry.
- Lacks rotational symmetry.
Details about Isosceles Trapezium:
- Isosceles trapeziums have specific attributes:
- One pair of unequal parallel sides.
- Two sides that are not parallel but equal in length.
- Two pairs of adjacent angles that are equal.
- Diagonals are of equal lengths in isosceles trapeziums.
- Possesses one line of symmetry.
- Does not have rotational symmetry.
Understanding an Isosceles Trapezium
- An isosceles trapezium is characterized by:
- One pair of unequal parallel sides.
- Two non-parallel equal sides.
- Two pairs of adjacent equal angles.
- Diagonals that are equal in length.
- One line of symmetry.
- No rotational symmetry.
Examples
- Parallelograms, kites, and trapeziums are quadrilaterals with distinct properties:
- They all have four sides and four angles.
- The lengths and positions of their edges help identify the type of quadrilateral.
Parallelograms, kites, and trapeziums have specific characteristics that differentiate them from other shapes. These properties help in recognizing and categorizing these quadrilaterals correctly.
- A parallelogram possesses:
- Two pairs of equal and parallel sides.
- When the side lengths are equal, it becomes a rhombus.
- Two pairs of equal angles with opposite angles being equal.
- Special cases include the rectangle (when angles are 90°) and square (when all sides and angles are 90°).
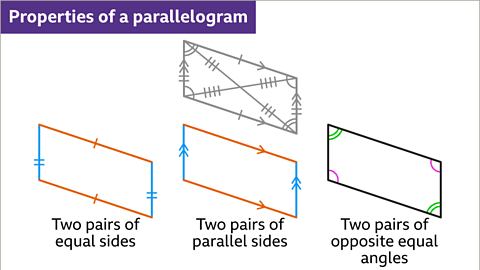
A detailed examination of a parallelogram showcases its unique features, such as equal sides, parallel sides, and opposite equal angles, along with special cases like the rhombus, rectangle, and square.
Properties of Parallelograms
- When the diagonals of a parallelogram bisect each other, the parallelogram is a rectangle.
Image Caption:
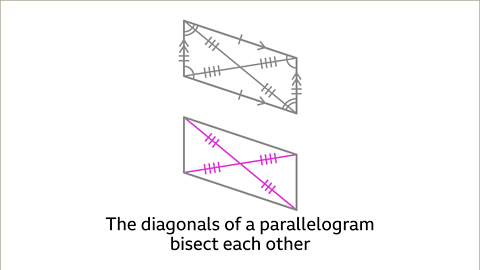
- Parallelograms have no line symmetry. They exhibit order 2 rotational symmetry and fit into their outline twice in a full turn.
Image Caption:
- A kite has two pairs of equal adjacent sides. When these sides are of equal length, the kite becomes a rhombus. Additionally, a kite features two equal angles.
Image Caption:
- The diagonals of a kite are perpendicular, intersecting at right angles. One diagonal bisects the other.
Image Caption:
Understanding Symmetry and Properties of Shapes
Kite Symmetry:
A kite possesses one line of symmetry, allowing it to be cut into two mirrored halves. It exhibits rotational symmetry of order 1, fitting into its outline in only one orientation, indicating no rotational symmetry.Trapezium Properties:
Every trapezium features one pair of unequal parallel sides. An isosceles trapezium has two equal sides and two pairs of equal adjacent angles.
Diagonals of Trapeziums:
The diagonals of an isosceles trapezium are of equal length, which distinguishes isosceles trapeziums from other trapeziums.Line Symmetry of Trapeziums:
An isosceles trapezium displays one line of symmetry, enabling it to be divided into mirrored halves. Unlike kites, trapeziums lack line or rotational symmetry.
Shapes and Their Properties
- Parallelogram, Kite, Trapezium, and Isosceles Trapezium are four types of shapes displayed in the images.
- All these shapes have four sides and four angles.
- Identification of these quadrilaterals is based on the lengths and positions of their edges.
Questions
Back to topIdentifying Types of Quadrilaterals Based on Their Characteristics
To recognize different quadrilaterals based on their properties, consider the following:
- Take into account known facts about quadrilaterals, such as:
- Equal side lengths
- Parallel sides
- Equal angles
- Diagonal properties
- Reflection symmetry
- Rotational symmetry
Remember that a single property might apply to various types of quadrilaterals.
Examples
Image gallerySkip image gallery- Consider the scenario where two lines are 3 cm long, and two lines are 5 cm long:
- For instance, if two pairs of opposite sides have equal lengths, the resulting quadrilaterals are a rectangle and a parallelogram:
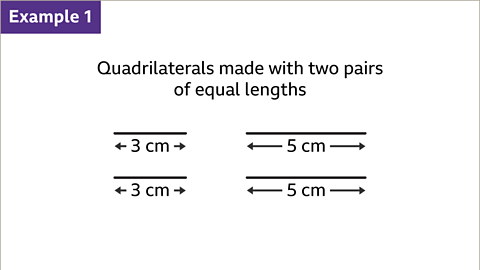
What types of quadrilaterals can be formed from these line lengths?
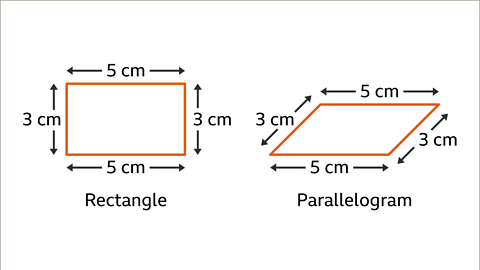
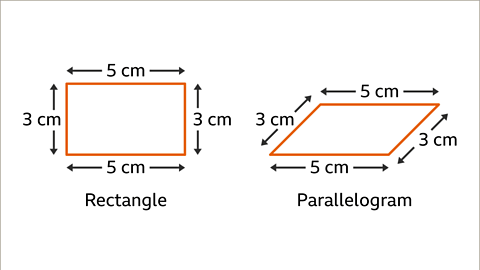
The rectangle has 90-degree angles, while the parallelogram has two pairs of equal opposite angles. Another unique quadrilateral can also be formed in this scenario.
Understanding Quadrilaterals and Diagonals
- Kite Quadrilaterals
- When two equal lines are adjacent, the quadrilateral forms a kite with two pairs of equal adjacent sides.
- Quadrilaterals with Bisection of Diagonals
- Identify quadrilaterals where diagonals bisect each other.
- Examples illustrate different cases of diagonals bisecting within quadrilaterals.
- Quadrilaterals with Equal Diagonal Lengths
- When diagonal lengths are equal, quadrilaterals may be squares or rectangles.
- Diagonals of a square bisect at right angles, while in a rectangle, they bisect without forming right angles.
- Illustrative images show squares and rectangles with equal diagonal lengths.
- Quadrilaterals with Unequal Diagonal Lengths
- When diagonal lengths differ, quadrilaterals could be rhombuses or parallelograms.
- Rhombus diagonals are unequal and bisect at right angles, whereas parallelogram diagonals also bisect but are unequal.
- Examples demonstrate rhombuses and parallelograms with unequal diagonal lengths.
Image Captions
- When the two equal lines are placed next to each other, the quadrilateral is a kite. A kite has two pairs of equal adjacent sides.
- Work out which quadrilateral has diagonals that bisect each other.
- When the diagonal lengths are equal, the quadrilateral may be a square or a rectangle. The diagonals of a square bisect each other at right angles. The diagonals of a rectangle bisect each other. The angles where the diagonals cross are not right angles, the opposite angles are equal. There are other quadrilaterals whose diagonals bisect each other.
- When the diagonal lengths are unequal, the quadrilateral may be a rhombus or a parallelogram. The diagonals of a rhombus are unequal and bisect each other at right angles. The diagonals of a parallelogram are unequal and bisect each other. The angles where the diagonals cross are not right angles, the opposite angles are equal.
Slide 1 of 6 - Example One
- Illustration: An image showing four straight lines with labeled lengths.
- Description: Two lines are 3 centimeters long, and the other two are 5 centimeters long.
- Characteristics: The lines form quadrilaterals with two pairs of equal lengths.
- Question: What types of quadrilaterals can be formed with two 3 cm lines and two 5 cm lines?
Explanation
In this scenario, when we have two lines measuring 3 cm and two lines measuring 5 cm, we are dealing with creating quadrilaterals. Let's delve into the possible types:
- Square: A square is a quadrilateral with all sides equal. If we use two 3 cm lines and two 5 cm lines, we cannot form a square since all sides must be equal in length.
- Rectangle: A rectangle is a quadrilateral with opposite sides equal and all angles at 90 degrees. Using two pairs of 3 cm and 5 cm lines, we can create a rectangle where opposite sides are equal.
- Parallelogram: A parallelogram is a quadrilateral with opposite sides parallel. With the given lengths, a parallelogram can be formed using the 3 cm and 5 cm lines.
- Rhombus: A rhombus is a quadrilateral with all sides equal. It's not possible to create a rhombus with two 3 cm and two 5 cm lines.
Key Takeaways
- Understanding the properties of different quadrilaterals helps identify the shapes that can be constructed with specific side lengths.
- By knowing the characteristics of squares, rectangles, parallelograms, and rhombuses, we can determine the possibilities when given specific line lengths.
For further clarity, it's essential to practice drawing these shapes and exploring how varying side lengths affect the types of quadrilaterals that can be formed.
Back to top
Practise finding the properties of quadrilaterals
Practise working out properties of quadrilaterals with this quiz. You may need a pen and paper to help you with your answers.
Quiz
Real-life maths

Properties of quadrilateral: A 2D shape with 4 edges and 4 vertices. Quadrilaterals can be important in design. All quadrilaterals can tessellate, meaning a single quadrilateral can be used to create a repeating pattern to cover a surface with no gaps. Geometric wallpaper and fabric designs often feature tessellating patterns.
- Quadrilaterals in Design:
- Quadrilaterals are fundamental shapes in various design software, including gaming, architecture, fashion, and laser printing.
- A 'basket weave' design for fabric, wallpaper, or web pages is created using rectangles.




















